强化学习经典算法笔记(九):LSTM加持的PolicyGradient算法
强化学习经典算法笔记(九):LSTM加持的PolicyGradient算法
在上文《强化学习经典算法笔记(八):LSTM加持的A2C算法解决POMDP问题》的基础上,实现了LSTM+MLP的Policy Gradient算法。
实现过程如下:
import argparse, math, os, sys
import numpy as np
import gym
from gym import wrappers
import matplotlib.pyplot as plt
import torch
from torch.autograd import Variable
import torch.autograd as autograd
import torch.nn.utils as utils
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
plt.ion()
parser = argparse.ArgumentParser(description='PyTorch REINFORCE example')
parser.add_argument('--env_name', type=str, default='LunarLanderContinuous-v2')
parser.add_argument('--gamma', type=float, default=0.99, metavar='G',
help='discount factor for reward (default: 0.99)')
parser.add_argument('--seed', type=int, default=123, metavar='N', # 随机数种子
help='random seed (default: 123)')
parser.add_argument('--num_steps', type=int, default=1000, metavar='N', # 一个episode最长持续帧数
help='max episode length (default: 1000)')
parser.add_argument('--num_episodes', type=int, default=2000, metavar='N', # 训练episode数量
help='number of episodes (default: 2000)')
parser.add_argument('--hidden_size', type=int, default=128, metavar='N', # 神经网络隐层神经元数量
help='number of episodes (default: 128)')
parser.add_argument('--render', action='store_true',
help='render the environment')
parser.add_argument('--ckpt_freq', type=int, default=100,
help='model saving frequency')
parser.add_argument('--display', type=bool, default=False,
help='display or not')
args = parser.parse_args()
env_name = args.env_name # 游戏名
env = gym.make(env_name) # 创建环境
if args.display:
env = wrappers.Monitor(env, '/tmp/{}-experiment'.format(env_name), force=True)
env.seed(args.seed) # 随机数种子
torch.manual_seed(args.seed) # Gym、numpy、Pytorch都要设置随机数种子
np.random.seed(args.seed)
class Policy(nn.Module): # 神经网络定义的策略
def __init__(self, hidden_size, num_inputs, action_space):
super(Policy, self).__init__()
self.action_space = action_space # 动作空间
num_outputs = action_space.shape[0] # 动作空间的维度
self.lstm = nn.LSTM(num_inputs, hidden_size, batch_first = True)
self.linear1 = nn.Linear(hidden_size, hidden_size) # 隐层神经元数量
self.linear2 = nn.Linear(hidden_size, num_outputs)
self.linear2_ = nn.Linear(hidden_size, num_outputs)
def forward(self, x, hidden):
x, hidden = self.lstm(x, hidden)
x = F.relu(self.linear1(x))
mu = self.linear2(x) # 为了输出连续域动作,实际上policy net定义了
sigma_sq = self.linear2_(x) # 一个多维高斯分布,维度=动作空间的维度
return mu, sigma_sq, hidden
class REINFORCE:
def __init__(self, hidden_size, num_inputs, action_space):
self.action_space = action_space
self.model = Policy(hidden_size, num_inputs, action_space) # 创建策略网络
# self.model = self.model.cuda() # GPU版本
self.optimizer = optim.Adam(self.model.parameters(), lr=1e-3) # 优化器
self.model.train()
self.pi = Variable(torch.FloatTensor([math.pi])) # .cuda() # 圆周率
def normal(self, x, mu, sigma_sq): # 计算动作x在policy net定义的高斯分布中的概率值
a = ( -1 * (Variable(x)-mu).pow(2) / (2*sigma_sq) ).exp()
b = 1 / ( 2 * sigma_sq * self.pi.expand_as(sigma_sq) ).sqrt() # pi.expand_as(sigma_sq)的意义是将标量π扩展为与sigma_sq同样的维度
return a*b
def select_action(self, state, hx, cx):
# mu, sigma_sq = self.model(Variable(state).cuda())
mu, sigma_sq, (hx,cx) = self.model(Variable(state),(hx,cx))
sigma_sq = F.softplus(sigma_sq)
eps = torch.randn(mu.size()) # 产生一个与动作向量维度相同的标准正态分布随机向量
# action = (mu + sigma_sq.sqrt()*Variable(eps).cuda()).data
action = (mu + sigma_sq.sqrt()*Variable(eps)).data # 相当于从N(μ,σ²)中采样一个动作
prob = self.normal(action, mu, sigma_sq) # 计算动作概率
entropy = -0.5*( ( sigma_sq + 2 * self.pi.expand_as(sigma_sq) ).log()+1 ) # 高斯分布的信息熵,参考https://blog.csdn.net/raby_gyl/article/details/73477043
log_prob = prob.log() # 对数概率
return action, log_prob, entropy, hx,cx
def update_parameters(self, rewards, log_probs, entropies, gamma):# 更新参数
R = torch.zeros(1, 1)
loss = 0
for i in reversed(range(len(rewards))):
R = gamma * R + rewards[i] # 倒序计算累计期望
# loss = loss - (log_probs[i]*(Variable(R).expand_as(log_probs[i])).cuda()).sum() - (0.0001*entropies[i].cuda()).sum()
loss = loss - (log_probs[i]*(Variable(R).expand_as(log_probs[i]))).sum() - (0.0001*entropies[i]).sum()
loss = loss / len(rewards)
self.optimizer.zero_grad()
loss.backward()
utils.clip_grad_norm_(self.model.parameters(), 40) # 梯度裁剪,梯度的最大L2范数=40
self.optimizer.step()
agent = REINFORCE(args.hidden_size, env.observation_space.shape[0], env.action_space)
dir = 'ckpt_' + env_name
if not os.path.exists(dir):
os.mkdir(dir)
log_reward = []
log_smooth = []
for i_episode in range(args.num_episodes):
state = torch.Tensor([env.reset()])
entropies = []
log_probs = []
rewards = []
hx = torch.zeros(args.hidden_size).unsqueeze(0).unsqueeze(0); # 初始化隐状态
cx = torch.zeros(args.hidden_size).unsqueeze(0).unsqueeze(0);
# print(hx.shape)
for t in range(args.num_steps): # 1个episode最长num_steps
# print(state.shape)
action, log_prob, entropy, hx, cx = agent.select_action(state.unsqueeze(0),hx,cx)
action = action.cpu()
next_state, reward, done, _ = env.step(action.numpy()[0,0])
entropies.append(entropy)
log_probs.append(log_prob)
rewards.append(reward)
state = torch.Tensor([next_state])
if done:
break
# episode结束,开始训练
agent.update_parameters(rewards, log_probs, entropies, args.gamma)
if i_episode%args.ckpt_freq == 0:
torch.save(agent.model.state_dict(), os.path.join(dir, 'reinforce-'+str(i_episode)+'.pkl'))
print("Episode: {}, reward: {}".format(i_episode, np.sum(rewards)))
log_reward.append(np.sum(rewards))
if i_episode == 0:
log_smooth.append(log_reward[-1])
else:
log_smooth.append(log_smooth[-1]*0.99+0.01*np.sum(rewards))
plt.plot(log_reward)
plt.plot(log_smooth)
plt.pause(1e-5)
env.close()
在LunarLanderContinuous-v2环境中,使用本文算法和vanilla PG算法进行训练,结果如下,优势明显。
PG+LSTM
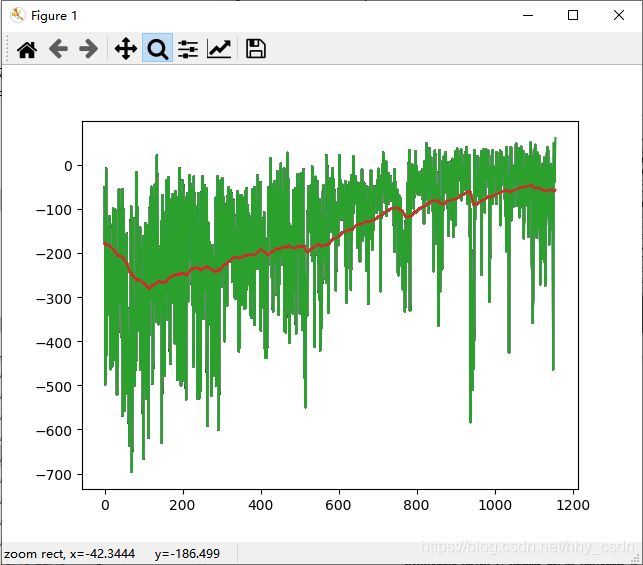
vanilla PG