2019/6/8CS231n课程笔记(优化与迁移学习)
目录
优化
1、梯度下降
(1)、动量,就给梯度下降加了个速度(助力)
(2)、对梯度进行处理:AdaGrad和RMSProp
(3)、结合了速度和平方梯度的方法Adam
2、学习率
3、另一种优化的思路:海森矩阵(牛顿定理)
总结:
4、model ensembly
正则化
1、使用正则项
2、Dropout
3、数据增强
4、其他的一些方法:
迁移学习
优化
1、梯度下降
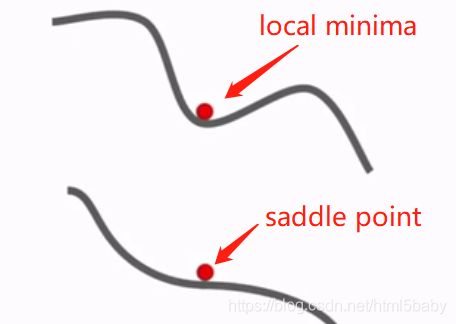
局部最小值和鞍点:局部最小值是在某一区域内出现的梯度最小值,而鞍点指的是梯度为0的点。在高维数据中,鞍点是常出现的一种情况,指的是在一些维数上loss是增大的,一些维数上loss是减小的。
为了解决这两种问题,引入了一种花哨的方法:
(1)、动量,就给梯度下降加了个速度(助力)
解决它因为某些噪声导致的局部最优梯度和鞍点就不再继续下降的问题。
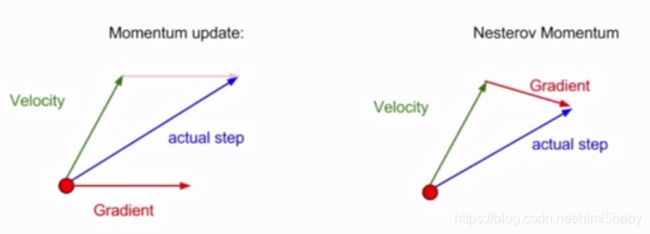
两种动量的方法:
普通的SGD动量:估算当前位置的梯度,然后取速度和梯度的混合
Nesterov 动量:在取得的速度的方向上步进,之后估计这一位置上的梯度,然后回到初始位置,将这两者混合起来。
(2)、对梯度进行处理:AdaGrad和RMSProp
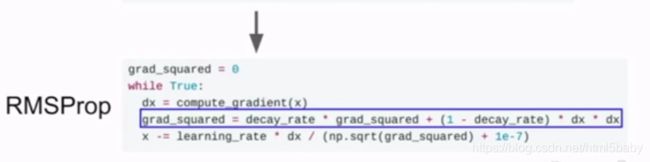
进行梯度平方项的一直累加。在更新参数向量的时候,除以这个梯度平方。对于小的向量梯度,在更新参数的时候除以更小的值使得梯度增加,大的梯度除以更大的值使得梯度减小。这种方法还是存在梯度被困在局部最优解中的问题,所以有提出了新的解决办法:RMSProp,和AdaGrad不同的是,这一次让平方梯度以一定的比率下降,这个比率叫衰减率。常设置为0.9或是0.99,用1-衰减率再和平方梯度相乘后加上衰减率乘原来的平方梯度
(3)、结合了速度和平方梯度的方法Adam
单单这样处理会出现一种情况,当first_moment很大,而second_moment接近于零的时候,刚开始的x将会很大,这个很大的步长对训练会产生较大的影响。所以adam有个偏执矫正项如下图所示,用来避免刚开始会出现的较大的步长。
2、学习率
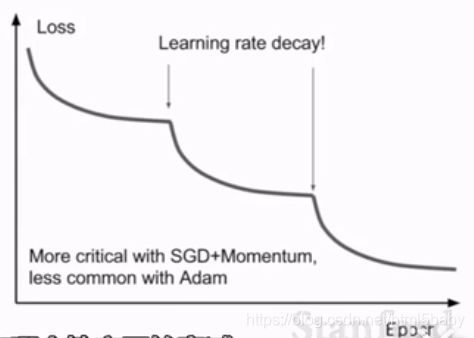
使用衰减的学习率,例如resnet,在某一时刻用衰减率对学习率进行调整。但这种方法并不能在训练初期就开始使用,在训练开始的时候还是要挑选一个合适的学习率,并观察loss的变化,进而决定在什么时候衰减学习率。
3、另一种优化的思路:海森矩阵(牛顿定理)
一种直接选择最小值进行梯度下降的方法。这种方法的优点是不需要使用学习率,缺点是计算量太大。
L-BFGS是一种近似于海森矩阵的方法。这种方法不是很实用,对于random的问题处理效果不好,对于非凸的情况表现很差。所以L-BFGS常在风格迁移的时候使用。
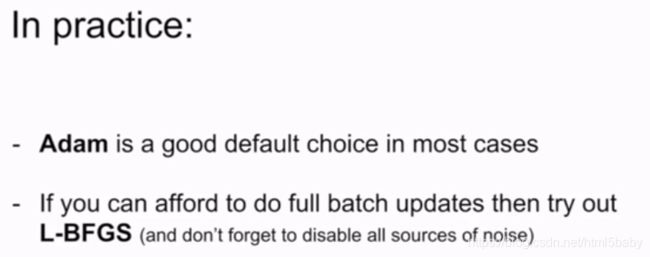
总结:
在深度学习中常用的还是Adam,L-BFGS要根据情况进行选择。
4、model ensembly
以上这些方法都是在减少训练中的loss、最小化目标函数,而还有一种情况是我们需要重视的,就是训练和测试之间的误差,对于这一类问题,我们选择使用模型集成的方法。
模型集成就是选择从不同的随机初始值上训练若干个(通常是10个)不同的模型,测试时,在这若干个模型上进行测试并平均10个模型的预测结果,能够缓解过拟合。
在训练过程使用一个模型的多个snapshot,能够在一次训练中得到很好的提升(不懂)
一种小技巧:使用Polyak平均。(不怎么常用,也没懂)
正则化
1、使用正则项
刚说了模型的集成,如果想在单个模型上面提高效果呢?使用正则化,这种方法能够有效地防止过拟合。以下是几种常见的正则化的方法:
解决过拟合问题除了利用添加正则项还可以使用Dropout的方法,将一部分激活函数值置零。
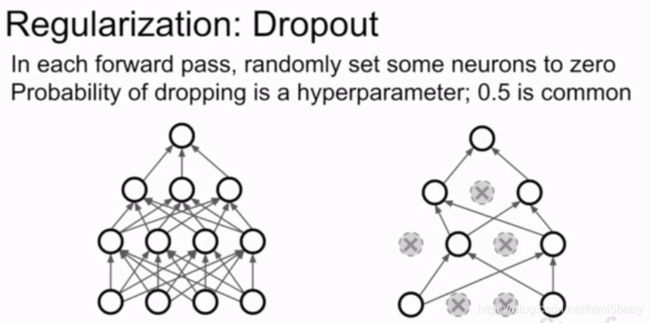
2、Dropout
通常在全连接层使用,但有时也在卷积层使用,在卷积层使用的时候是将整个维度的一组特征值置零。使用dropout会使训练时间边长但是能够增加鲁棒性。
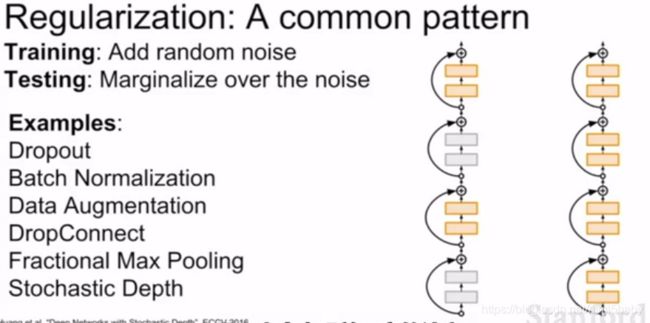
因为Dropout的作用,我们的输出有了随机性(什么意思??)。在测试阶段想通过积分的方式来边缘化这种随机性。
当我们计算dropout后的解析值,发现假设dropout的概率为0.5,在训练阶段和测试时的平均值差0.5倍,是不匹配的。
所以使用dropout训练后,用dropout的概率乘测试阶段的输出值。
如果想要test的时间不受影响,那就在train的时候除上dropout的值。毕竟train是在GPU上进行的。
正则化和批量归一化都是较为常见的正则化方法,相比批量归一化dropout有dropout的概率可以控制正则化的强度。
3、数据增强
对数据及进行相应的变换啊处理啊balabala的。平移、旋转、伸缩、裁剪等等等等等。
色彩抖动??(没见过,等可能用到的时候再说)
4、其他的一些方法:
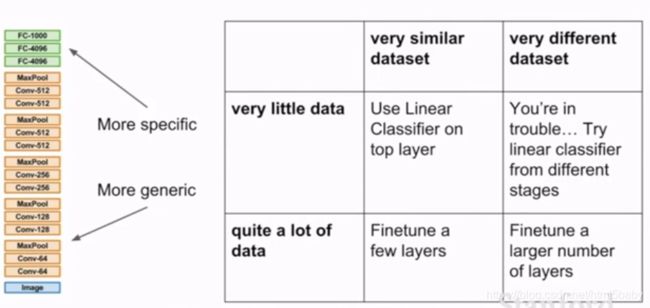
迁移学习
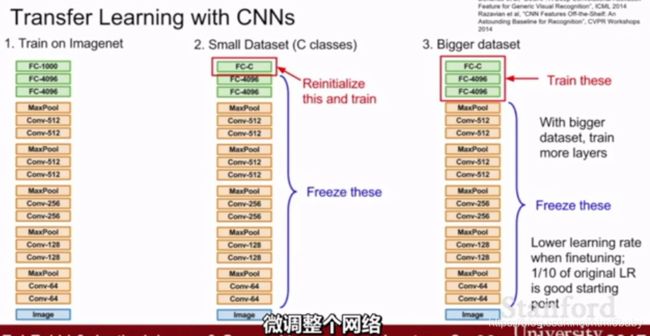
对于数据集大小的不同进行微调的位置也不同,小的数据集就在最后分类的全连接层进行重新的训练,大的数据集在后几个全连接层进行重新训练。
根据数据集之间的相似度的大小,进行微调的位置也有所不同。相似度小的话,就需要重新训练大部分的结构了……