python不使用框架实现卷积神经网络识别手写数字

网络结构

项目下载地址
不使用框架实现全连接神经网络实现手写数字识别(layer封装好, 可以很好的扩展,修改)

• 第一个卷积层输入：2828、一通道、滤波器55个数为 6个、步长为1、不补零。
• 第一个卷积层输出：24*24、深度为6。
• 第一个池化层输入：2424、6通道、滤波器22，步长为2。
• 第一个池化层输出：12*12，深度为6。
• 第二个卷积层输入：1212，6通道，滤波器55个数为12个，步长为1，不补零。
• 第二个卷积层输出：8*8、深度为12.。
• 第二个池化层输入：88，12通道，滤波器22，步长为2。
• 第二个池化层输出： 44，深度为12，共44*12=192个像素。
• 第一个全连接层：输入为192，输出为10,10个节点，采用softmax激活函数，前面均采用双曲正切函数作为激活函数。

数据集

mnist数据集
t10k-images.idx3-ubyte
t10k-labels.idx1-ubyte
train-images.idx3-ubyte
train-labels.idx1-ubyte
下载

训练结果

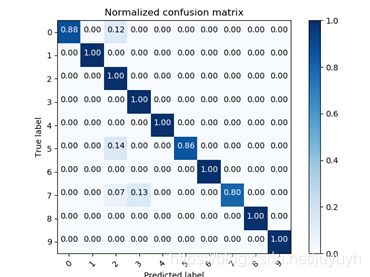
混淆矩阵

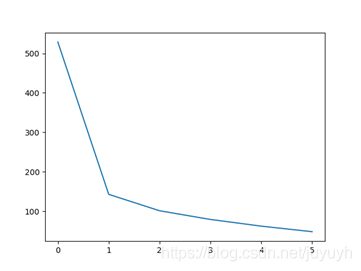
损失曲线

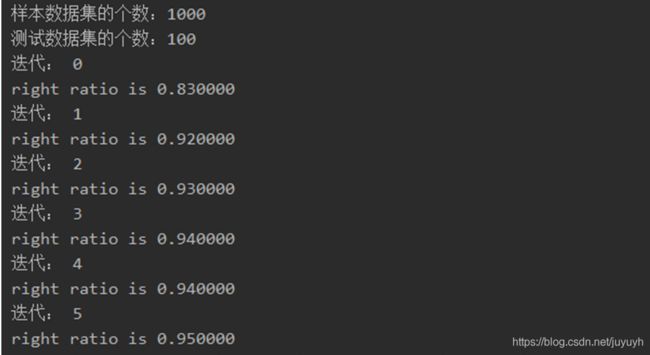
运行结果

在100个的测试集上准确率最高可达95%。

# 使用全连接神经网络类，和手写数据加载器，实现验证码识别。
import numpy as np
import Activators  # 引入激活器模块
import CNN  # 引入卷积神经网络
import MNIST_loader  # 引入手写数据加载器
import DNN  # 引入全连接神经网络


# 网络模型类
class MNISTNetwork():
    # =============================构造网络结构=============================
    def __init__(self):
        # 初始化构造卷积层：输入宽度、输入高度、通道数、滤波器宽度、滤波器高度、滤波器数目、补零数目、步长、激活器、学习速率
        # 输入28*28 一通道，滤波器5*5的6个，步长为1，不补零，所以输出为24*24深度6
        self.cl1 = CNN.ConvLayer(28, 28, 1, 5, 5, 6, 0, 1, Activators.TanhActivator(), 0.02)
        # 构造降采样层，参数为输入宽度、高度、通道数、滤波器宽度、滤波器高度、步长
        self.pl1 = CNN.MaxPoolingLayer(24, 24, 6, 2, 2, 2)  # 输入24*24，6通道，滤波器2*2，步长为2，所以输出为12*12，深度保持不变为6
        # 初始化构造卷积层：输入宽度、输入高度、通道数、滤波器宽度、滤波器高度、滤波器数目、补零数目、步长、激活器、学习速率
        # 输入12*12，6通道，滤波器5*5的12个，步长为1，不补零，所以输出为8*8深度12
        self.cl2 = CNN.ConvLayer(12, 12, 6, 5, 5, 12, 0, 1, Activators.TanhActivator(), 0.02)
        # 构造降采样层，参数为输入宽度、高度、通道数、滤波器宽度、滤波器高度、步长
        self.pl2 = CNN.MaxPoolingLayer(8, 8, 12, 2, 2, 2)  # 输入8*8，12通道，滤波器2*2，步长为2，所以输出为4*4，深度保持不变为12。共192个像素
        # 全连接层构造函数。input_size: 本层输入向量的维度。output_size: 本层输出向量的维度。activator: 激活函数
        self.fl1 = DNN.FullConnectedLayer(192, 10, Activators.SoftmaxActivator(), 0.02)  # 输入192个像素，输出为10种分类概率,学习速率为0.05

    # 根据输入计算一次输出。因为卷积层要求的数据要求有通道数，所以onepic是一个包含深度，高度，宽度的多维矩阵
    def forward(self, onepic):  # 池化层不改变深度，只改变宽高  因为池化层的计算是一层一层的提取运算的
        # print('图片：',onepic.shape)
        self.cl1.forward(onepic)  # 返回值6*24*24深度，高度，宽度  即self.cl1.output_array   卷积核为1*5*5    6*24*24
        # print('第一层卷积结果：',self.cl1.output_array.shape)
        self.pl1.forward(self.cl1.output_array)  # 通过最大池化层后，深度不变仍为6 ，卷积核为 2*2 尺寸改变  self.pl1.output_array 6*12*12
        # print('第一层采样结果：',self.pl1.output_array.shape)
        self.cl2.forward(self.pl1.output_array)  # 卷积核为 6*5*5  计算之后尺寸为 self.cl2.output_array 12*8*8
        # print('第二层卷积结果：',self.cl2.output_array.shape)
        self.pl2.forward(self.cl2.output_array)  # 卷积核为 12*2*2  深度不变仍为12  计算之后尺寸为 self.pl2.output_array 12*4*4
        # print('第二层采样结果：',self.pl2.output_array.shape)
        # 转化为列向量  结果为12*4*4=192  a是个矩阵或者数组，a.flatten()就是把a降到一维，默认是按横的方向降
        flinput = self.pl2.output_array.flatten().reshape(-1, 1)
        # print(self.pl2.output_array.shape[0])
        # print(self.pl2.output_array.shape[1])
        # print(self.pl2.output_array.shape[2])
        # print(len(flinput))
        # print(flinput.shape)
        self.fl1.forward(flinput)  # flinput尺寸为192*1，全连接层的w是10*192
        # print('全连接层结果：',self.fl1.output)#self.fl1.output尺寸为 10*1  因为经过了 W*t+b   W为10*192
        return self.fl1.output

    def backward(self, onepic, labels):
        # 计算误差
        '''
            output = tanh(z)
            f'(z) = 1 - tanh(z)^2
            delta = (y_pred - y)*f'(z)
        '''
        # 最后一层采用softmax函数
        delta = labels - self.fl1.output
        # 反向传播
        self.fl1.backward(delta)  # 计算了全连接层输入前的误差，以及全连接的w和b的梯度   误差传递公式 error_j=W.T点乘error_k   self.fl1.delta=
        self.fl1.update()  # 更新全连接层的权重w和偏量b
        # print('全连接层输入误差：', self.fl1.delta.shape)
        sensitivity_array = self.fl1.delta.reshape(
            self.pl2.output_array.shape)  # 将误差转化为同等形状  self.pl2.output_array 形状为12*4*4
        self.pl2.backward(self.cl2.output_array, sensitivity_array)  # 计算第二采样层的输入误差。参数为第二采样层的 1、输入，2、输出误差
        # print('第二采样层的输入误差：', self.pl2.delta_array.shape)
        self.cl2.backward(self.pl1.output_array, self.pl2.delta_array,
                          Activators.TanhActivator())  # 计算第二卷积层的输入误差。参数为第二卷积层的 1、输入，2、输出误差，3、激活函数
        self.cl2.update()  # 更新权重w和偏量b 6*12*12          12*8*8
        self.pl1.backward(self.cl1.output_array, self.cl2.delta_array)  # 计算第一采样层的输入误差。参数为第一采样层的 1、输入，2、输出误差
        self.cl1.backward1(onepic, self.pl1.delta_array,
                           Activators.TanhActivator())  # 计算第一卷积层的输入误差。参数为第一卷积层的 1、输入，2、输出误差，3、激活函数
        self.cl1.update()  # 更新权重w和偏量b
        # print('第一卷积层的输入误差：', self.cl1.delta_array.shape)


# 由于使用了逻辑回归函数，所以只能进行分类识别。识别ont-hot编码的结果
if __name__ == '__main__':
    # =============================加载数据集=============================
    # 加载训练样本数据集，和one-hot编码后的样本标签数据集。样本数量越大，训练时间越久，也越准确
    train_data_set, train_labels = MNIST_loader.get_training_data_set(1000, False)
    # print(type(train_data_set))    
    # 加载测试特征数据集，和one-hot编码后的测试标签数据集。训练时间越久，也越准确
    test_data_set, test_labels = MNIST_loader.get_test_data_set(100, False)

    train_data_set = np.array(train_data_set).astype(bool).astype(int)  # 可以将图片简化为黑白图片
    train_labels = np.array(train_labels)

    # 可以将图片简化为黑白图片  将数据转化为bool布尔型，True  false  进而转化为0、1数据
    test_data_set = np.array(test_data_set).astype(bool).astype(int)
    test_labels = np.array(test_labels)

    print('样本数据集的个数：%d' % len(train_data_set))
    print('测试数据集的个数：%d' % len(test_data_set))

    # =============================构造网络结构=============================
    mynetwork = MNISTNetwork()
    losses = []
    # =============================迭代训练=============================
    for i in range(6):  # 迭代训练10次。每个迭代内，对所有训练数据进行训练，更新（训练图像个数/batchsize）次网络参数
        print('迭代：', i)
        # 使用每一个样本进行训练image.shape[0]#图片垂直尺寸image.shape[1]#图片水平尺寸image.shape[2]#图片通道数

        loss = 0
        for k in range(train_data_set.shape[0]):
            # 正向计算
            onepic = train_data_set[k]
            onepic = np.array([onepic])  # 卷积神经网络要求的输入必须包含深度、高度、宽度三个维度。
            result = mynetwork.forward(onepic)  # 前向计算一次
            # print(result.flatten())
            labels = train_labels[k].reshape(-1, 1)  # 获取样本输出，转化为列向量
            # print(labels)
            mynetwork.backward(onepic, labels)
            s_max = result[np.argmax(result)]
            loss += -1 * np.log(s_max)
        losses.append(loss)

        # =============================评估结果=============================
        right = 0
        for k in range(test_data_set.shape[0]):  # 使用每一个样本进行训练
            # 正向计算
            onepic = test_data_set[k]
            onepic = np.array([onepic])  # 卷积神经网络要求的输入必须包含深度、高度、宽度三个维度。
            result = mynetwork.forward(onepic)  # 前向计算一次
            labels = test_labels[k].reshape(-1, 1)  # 获取样本输出，转化为列向量
            # print(result)
            pred_type = result.argmax()
            real_type = labels.argmax()

            # print(pred_type,real_type)
            if pred_type == real_type:
                right += 1

        print('right ratio is %f' % (right / test_data_set.shape[0]))  # 打印输出正确率

    # 画损失曲线
    from CNN1 import paint_tools
    print(losses)
    paint_tools.paint_loss_curve(losses)

    # 画混淆矩阵
    cnf_matrix = np.array([
        [0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
    ])

    for k in range(test_data_set.shape[0]):
        # 正向计算
        onepic = test_data_set[k]
        onepic = np.array([onepic])
        result = mynetwork.forward(onepic)
        labels = test_labels[k].reshape(-1, 1)
        # print(result)
        pred_type = result.argmax()
        real_type = labels.argmax()
        cnf_matrix[real_type][pred_type] += 1

    class_names = ['0', '1', '2', '3', '4', '5', '6', '7', '8', '9']
    paint_tools.plot_confusion_matrix(cnf_matrix, classes=class_names, normalize=True, title='Normalized confusion matrix')

项目下载地址