详解python实现markerless增强现实
文章目录
- 1.本文介绍
- 1.1 传统marker增强现实和markerless增强现实
- 1.2 实现源码能获得什么,为什么要写这篇文章
- 2.代码思路
- 3.源码地址
- 4.总结和展望
1.本文介绍
1.1 传统marker增强现实和markerless增强现实
传统marker的优点是非常稳定不抖动。缺点总结如下:
1.必须采用人工制作的固定样式的图像
2.必须将边缘展示出来,不能遮挡边缘的边和角
注:对于传统marker,opencv有个封装好的库叫做Aruco
markerless的优点如下:
1.只需要纹理丰富的图像
2.可以遮挡部分图像,不影响最后效果
缺点是抖动比较厉害。
为什么会有这样的特点,看懂了此文后半部分你就明白了
1.2 实现源码能获得什么,为什么要写这篇文章
网络上有很多这样的代码实现,且但普遍不太好学习。要么是c版本的,,要么集成到了别的软件里面,要么还调用了很多不易使用的库。直接放出代码的较多,对代码进行解析的比较少,在学习过程中我还发现了不少的错误理解和不为人所注意的关键点。比如比值测试,很多blog要么不说,要么简单理解为是一种匹配优化算法。再比如,如何说清楚外参矩阵,如何进行推导,以及如何通过外参矩阵计算出虚拟物体增强现实的位置。
2.代码思路
这里讲解总体思路:
1.由于颜色信息受光照影响很大,我们最好不考虑颜色信息。将图像灰度化
2.使用一种算法分别对模版图和目标图提取特征点,我采用orb或者sift,注意需要将图像缩放到统一大小。这里有个问题,理论上sift具有尺度不变的特性,但是实践发现不统一大小匹配图像特征点时效果比较差。
if self.alg == 'orb':
orb = cv2.ORB_create()
kp2, des2 = orb.detectAndCompute(self.frame, None) # kp2: keypoints from the frame/captured image
FLANN_INDEX_LSH = 6
index_params= dict(algorithm = FLANN_INDEX_LSH,
table_number = 6, # 12
key_size = 12, # 20
multi_probe_level = 1) #2
elif self.alg == 'sift':
FLANN_INDEX_KDTREE = 1
sift = cv2.xfeatures2d.SIFT_create()
kp2, des2 = sift.detectAndCompute(self.frame, None) # kp2: keypoints from the frame/captured image
index_params = dict(algorithm = FLANN_INDEX_KDTREE, trees = 5)
3.接下来就是对比模版图像和目标图像的特征点,这个阶段的目标是可以匹配到4以上个相同的特征点。我们可以这样看待这个问题,在一幅图中我们有n个点,在另一幅我们需要匹配的图中有m个点,我们的目标是找到这两个图中相同的4以上个点(4个是npnp计算位置的要求,后面会介绍)。我们发现这个问题可以用knn算法进行匹配。knn分类原理和一个二维码识别例子
由于图像提取特征点数量很大,knn匹配速度会比较慢,我们采用flann来优化速度flann原理
flann = cv2.FlannBasedMatcher(index_params, search_params)
try:
matches = flann.knnMatch(des1,des2,k=2)
except Exception as e:#把这个地方处理一下,准备
return None
knn中k=2意味着会返回特征距离最近的两个点,也就是说我们需要在两个点里面找到最相近的一个点。
很多同学不明白这一点,为什么不把k设置为1,返回最相近的1个点呢?实践过程中,我们发现k=1的情况下,非常容易出现错误匹配的问题,而且一个点可能出现匹配多个相似点。为了改进这个问题,我们采用比值测试。比值测试是指首先获取与A距离最近的点B(最近)和C(次近),只有当B/C小于阈值(0.75)才被认为是匹配。这么说可能还是不容易理解,详细来说说:我们在图像特征提取的时候,一块图像周围的特征点具有很大的相似性,我们首先通过knn,找到最近的两个,然后计算这两个点的距离是不是接近。假设两个点距离相差很大则认为是错误匹配,可能是同一个图像块在大图上的重复,比如两个相同的字。而如果距离相近,选择其中一个即可。
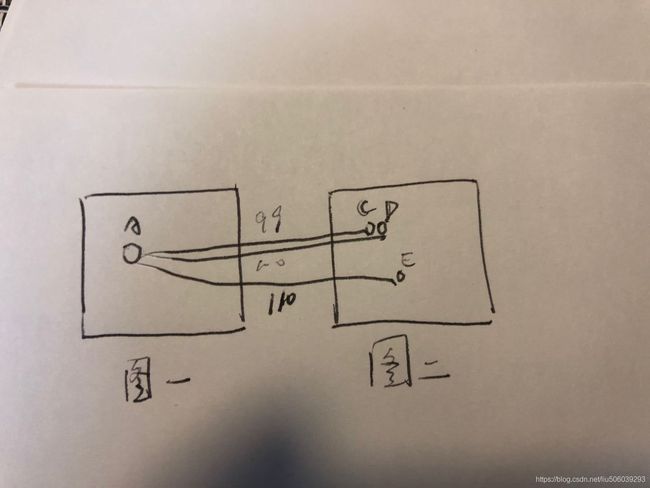
如图一中A点匹配图二中2个最近C,D,距离为99 100,则可以认为距离相近,是成功的匹配。如果是匹配C,E或者D,E,就是错误匹配。
4.接下来由于这一块内容十分不容易理解,我会尽量避免出现公式。
4.1通过匹配出来的这一大堆点来进行计算出两张图像的位置差别,这个差别我们用旋转平移矩阵来描述。

图像A

图像B
如上图所示,图像A示我们的目标模版图,图像B是我们的在摄像头中看到的图。事实上,图像B就是图像A的透视变换,opencv中有一个函数findHomography可以帮助我们计算出这个变换。
M, _ = cv2.findHomography(src_pts, dst_pts, cv2.RANSAC,5.0)
M为我们求的的矩阵,其中src_pts, dst_pts为我们在第三步找到的对应的特征点,RANSAC为拟合这个矩阵采用的优化方法。
4.2 我们设模版图周围四个角点的位置为(0,0)(0,h)(w,0)(w,h),将这4个点乘上M就可以得到图2四周的点。


4.3最最关键的是这一步,我们设图一在三维坐标的坐标值为[0,0,0],[w,0,0],[w,h,0],[0,h,0],也就是说我们把图一的四个坐标点转换到了z平面上。我们不讨论数学上的推导,仔细感受一下。这两钟坐标一个是二维,一个是三维,他们之间是不是存在一种对应关系呢?是否可以一一对应呢?是的!
本质上这种关系也是一个矩阵,可以用opencv中solvepnp来计算。
retval, rvec, tvec = cv2.solvePnP(src, dst, self.cameraMatrix, self.distCoeffs)
src,dst为二维和三维坐标。后两个参数一个是相机内参,一个是相机参数,均由相机光学性质所决定,可以通过标定获得。
4.4 最后一步就是将虚拟物体绘制在图2上了。我们只需要将内参,外参矩阵和三维坐标三者相乘,即可得到在图2上应该渲染出的三维物体的二维投影。
3.源码地址
回杭州传
4.总结和展望
markerless实现增强现实最为重大的缺点抖动。这是因为受光照变化,摄像头硬件条件不足等约束,特征点变化不定,而外参变化矩阵依赖于特征点。我们所做的大部分工作,就是为了尽可能的减少特征点变化带来的影响。从这点上来看,采用深度学习具有很大的前景。
简历上会更加深入探讨这一点,包含两方面
1.使用深度学习中的目标检测,分割等网络改进效果以及遇到的问题。
2.使用深度学习三维物体检测来改进。