LeetCode题解：寻找缺失的整数（异或运算）

寻找缺失的整数

题目：

一个无序数组里有99个不重复正整数，范围从1到100，唯独缺少一个整数。如何找出这个缺失的整数？

• 解法1:

  创建一个哈希表，以1到100这100个 整数为Key。然后遍历整个数组，每读到-一个整数，就定位到哈希表中对应的Key，然后删除这个Key。

  由于数组中缺少1个整数，哈希表最终一定会 有99个Key被删除，从而剩下1个唯一的Key。这个剩下的Key就是那个缺失的整数。

  假设数组长度是n，那么该解法的时间复杂度是0(n)，空间复杂度是0(n)。

缺点： 时间上是最优的，但是额外开辟了内存空间

• 解法2:

  先把数组元素从小到大进行排序，然后遍历已经有序的数组，如果发现某两个相邻元素并不连续，说明缺少的就是这两个元素之间的整数。

  假设数组长度是n，如果用时间复杂度为O(nlogn)的排序算法进行排序，那么该解法的时间复杂度是O(nlogn),空间复杂度是0(1)。

缺点：没有额外开辟空间，但是时间复杂度又太大了

• 解法3:

  这是一个很简单也很高效的方法，先算出1+2+3+…+100的和， 然后依次减去数组里的元素，最后得到的差值，就是那个缺失的整数。

  假设数组长度是n，那么该解法的时间复杂度是0(n)，空间复杂度是0(1)。

问题扩展：

• 题目：
  一个无序数组里有若干个正整数，范围是1-100，其中99个整数都出现了偶数次，只有1个整数出现了奇数次，如何找到这个出现奇数次的整数？

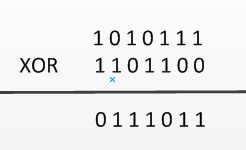
• 思路关键：异或运算（相同为0，不同为1）
  只需要把数组里所有元素依次进行异或运算，最后得到的就是那个缺失的整数！

• 解法：时间复杂度：O(n)，空间复杂度：O(1)

遍历整个数组，依次做异或运算。由于异或运算在进行位运算时，相同为0， 不同为1，因此所有出现偶数次的整数都会相互抵消变成0，只有唯一出现 奇数次的整数会被留下。

让我们举一个例子: 给出一个无序数组{3,1,3,2,4,1,4}。

异或运算像加法运算一样，满足交换律和结合律，所以这个数组元素的异或运算的结果如下所示。

3 xor 1 xor 3 xor 2 xor 4 xor 1
= 1 xor 1 xor 3 xor 3 xor 4 xor 4
=2

问题：如果数组里有2个整数出现了奇数次，其他整数出现了偶数次，则如何找出这2个整数呢？

题目第2次扩展:

题目：

假设一个无序数组里有若干个正整数，范围是1~ 100，其中有98个整数出现了偶数次，只有2个整数出现了奇数次，如何找到这2个出现奇数次的整数?

• 思路关键：分治法（把数组元素依次进行异或运算，得到的结果是2个出现了奇数次的整数的异或运算结果，在结果中至少有1个二进制位是1）

• 解法：时间复杂度：O(n)，空间复杂度：O(1)

把2个出现了奇数次的整数命名为A和B。遍历整个数组，然后依次做异或运算，进行异或运算的最终结果，等同于A和B进行异或运算的结果。在这个结果中，至少会有一个二进制位是1 (如果都是0，说明A和B相等，和题目不相符)。

举个例子，给出一个无序数组{4,1,2,2,5,1,4,3},所有元素进行异或运算的结果是00000110B。
4 xor 1 xor 2 xor 2 xor 5 xor 1 xor 4 xor 3
= 1 xor 1 xor 2 xor 2 xor 4 xor 4 xor 3 xor 5
= 3 xor 5
= 0000 0110B

选定该结果中值为1的某一位数字， 0000 0110B的倒数第2位是1，这说明A和B对应的二进制的倒数第2位是不同的。其中必定有一一个整数的倒数第2位是0， 另一个整数的倒数第2位是1。

根据这个结论，可以把原数组按照二进制的倒数第2位的不同，分成两部分，一部分的倒数第2位是0，另一部分 的倒数第2位是1。由于A和B的倒数第2位不同，所以A被分配到其中一部分，B被分配到另一部分， 绝不会出现A和B在同一部分， 另一部分既没有A，也没有B的情况。

则，转换到了原先的异或问题，找出唯一的奇数次整数即可。

代码实现：

package some_problem;/**
 * Copyright (C), 2019-2020
 * author  candy_chen
 * date   2020/8/4 20:25
 * version 1.0
 * Description: 寻找缺失的整数
 */

/**
 *一个无序数组里有99个不重复正整数，范围从1到100，唯独缺少一个整数。如何找出这个缺失的整数？
 */
public class FindLostNum {
    public static int[] findLostNum(int[] array){
        //用于存储2个出现奇数次的整数
        int result[] = new int[2];
        //第1次进行整体异或运算
        int xorResult = 0;
        for (int i=0;i<array.length;i++){
            xorResult ^= array[i];
        }
        //如果进行异或运算的结果为0，则说明输入的数组不符合题目要求
        if (xorResult == 0){
            return null;
        }
        //确定2个整数的不同为，以此来做分组
        int separator = 1;
        while (0==(xorResult&separator)){
            separator<<=1;
        }
        //第2次分组进行异或运算
        for (int i=0;i<array.length;i++){
            if (0==(array[i]&separator)){
                result[0]^=array[i];
            }else {
                result[1]^=array[i];
            }
        }
        return result;
    }

    public static void main(String[] args) {
        int[] array = {4,1,2,2,5,1,4,3};
        int[] result = findLostNum(array);
        System.out.println(result[0] + "," + result[1]);
    }
}

---

说明：作者根据网络资料进行搜索学习，理解整理 若有侵权联系作者
参考：程序员小灰