集成学习笔记整理1

集成学习（集成方法）是一种解决问题的思想（不是具体的算法）。操作为将若干个基本评估器(分类器&回归器)进行组合，然后使用这些基本评估器来综合对未知样本进行预测。通过这种“集思广益”的行为，比起使用单个基本评估器进行预测，集成学习具有更好的泛化能力与稳健性。

1. 集成学习分类

集成学习可以分为以下两类：

• 平均方法
  训练多个独立的基本评估器（评估器之间没有关联），然后对多个评估器的预测结果进行平均化。如果是分类任务，则使用多个评估器预测结果中，类别最多的作为预测结果。如果是回归任务，则使用多个评估器预测结果的均值作为预测结果。
  平均方法通过综合考量的行为，可以有效的减少方差，因此，其预测结果通常可以优于任何一个基本评估器。
• 增强方法
  多个基本评估器是按顺序训练的，然后将若干个模型（通常是弱评估器）进行组合，进而产生一个预测能力强的模型。与平均方法不同，增强方法的多个基本评估器不是独立的，后续评估器需要依赖于之前评估器，训练过程中，会试图减少组合之后评估器的偏差。

2. 集成学习效果

我们以二分类为例，如果存在n个分类器，每个分类器的错误率都为e且各个分类器之间是独立的。因此，多个分类器集成之后的错误率服从二项分布，其中，k个分类器出错的概率密度可表示为：
$P(y=k)=C_n^k{e}^k(1-e{)}^{n-k}$
假设现有11个分类器，单个分类器的错误率为0.25，则如果集成分类器出错，则至少需要6个（或6个以上）的分类器出错，集成后分类器出错的概率密度为：
$P(y⩾k)={\sum }_{k=6}^n{C}_{11}^{k}0.25^k\ast 0.75^{11-k}=0.034$
可见，集成后分类器的出错率要远小于单个分类器的出错率。

# 计算组合值。
from scipy.special import comb
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt

mpl.rcParams["font.family"] = "SimHei"
mpl.rcParams["axes.unicode_minus"] = False

# 用来计算集成分类器发生错误的概率密度值。
# n：基本评估器的数量。
# error：每一个基本评估器发生错误的概率。
def ensemble_error(n, error):
    # 如果要使集成评估器预测错误，则需要半数以上的基本评估器发生错误。
    # 这里计算半数评估器的值。
    start = np.ceil(n / 2.0)
    # 计算令集成评估器发生错误，基本评估器错误个数的区间。
    k = np.arange(start, n + 1)
    v = comb(n, k) * error ** k * (1-error) ** (n - k)
    return np.sum(v, axis=1)

# 定义基本评估器发生错误的概率区间。
error = np.arange(0.0, 1.01, 0.01)
# 计算在不同error取值的情况下，集成评估器发生错误的概率。
ens_errors = ensemble_error(n=11, error=error[:, np.newaxis])
plt.plot(error, ens_errors, label="集成分类器")
plt.plot(error, error, linestyle="--", label="基本分类器")
plt.xlabel("基本分类器错误率")
plt.ylabel("基本/集成分类器错误率")
plt.legend(loc="best")
plt.title("集成分类器效果")
plt.grid()
plt.show()

def ensemble_error(n, error):
    # 如果要使集成评估器预测错误，则需要半数以上的基本评估器发生错误。
    # 这里计算半数评估器的值。
    start = np.ceil(n / 2.0)
    # 计算令集成评估器发生错误，基本评估器错误个数的区间。
    k = np.arange(start, n + 1)
    v = comb(n, k) * error ** k * (1-error) ** (n - k)
    print(v)
    return np.sum(v, axis=1)

ensemble_error(11, np.array([[0.25], [0.35]]))

3. Bagging

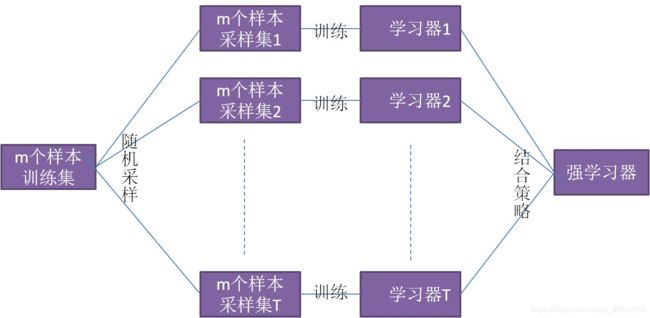
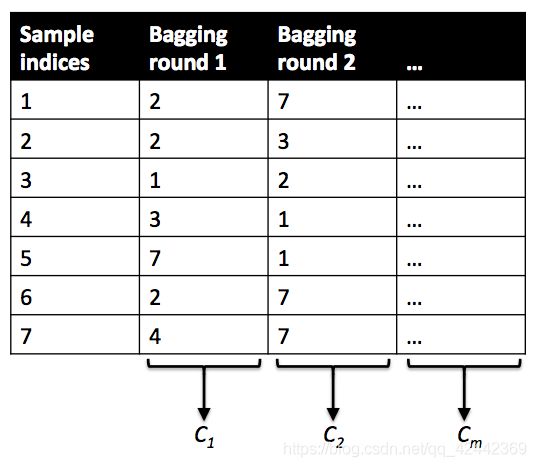
Bagging方法也称为汇聚法(Bootstrap Aggregating)，该模型是一种元评估器。方法过程为：在原始数据集上进行随机抽样（抽样可以是放回抽样与不放回抽样），使用得到的随机子集来训练评估器，该过程重复若干次。然后使用得到的若干个评估器（一次训练获取一个评估器），最后聚合每个单独的评估器的预测，形成最终的预测结果。
预测会使用多数投票（分类）或者求均值（回归）的方式来统计最终的结果（平均方法）。

3.1 优势

bagging方法通过随机抽样来构建原始数据集的子集，来训练不同的基本评估器，然后再将多个基本评估器进行组合来预测结果，这样可以有效减小基本评估器的方差。因此，通过bagging方法，就可以非常便捷的对基本评估器进行改进，而无需去修改基本评估器底层的实现。
因为bagging方法可以有效的降低过拟合，因此，bagging方法适用于强大而复杂的模型。

3.2 bagging分类示例

from sklearn.datasets import make_classification
from sklearn.linear_model import LogisticRegression
# sklearn.ensemble 该模块存放的都是关于集成算法相关的内容。 
# BaggingClassifier sklearn中提供用于分类的bagging模型。
# RandomForestClassifier sklearn中体用用于分类的随机森林模型。
from sklearn.ensemble import BaggingClassifier, RandomForestClassifier
from sklearn.model_selection import train_test_split

X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_classes=3, random_state=0)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=0)

lr = LogisticRegression()
lr.fit(X_train, y_train)
print("逻辑回归准确率：")
print(lr.score(X_train, y_train))
print(lr.score(X_test, y_test))
print("bagging准确率：")
# base_estimator：指定基本评估器。即bagging算法所组合的评估器。
# n_estimators：基本评估器的数量。（有多少个评估器，就会进行多少次随机采样，就会产生多少个原始数据集的子集。）
# max_samples：每次随机采样的样本数量。该参数可以是int类型或float类型。如果是int类型，则指定采样的样本数量。
# 如果是float类型，则指定采样占原始数据集的比例。
# max_features：每次随机采样的特征数量。可以是int类型或float类型。
# bootstrap：指定是否进行放回抽样。默认为True。
# bootstrap_features：指定对特征是否进行重复抽取。默认为False。
bag = BaggingClassifier(lr, n_estimators=100, max_samples=0.5, max_features=0.75)
bag.fit(X, y)
print(bag.score(X_train, y_train))
print(bag.score(X_test, y_test))
print("随机森林准确率：")
# n_estimators：随机森林评估器（决策树）的数量。
# criterion不存度度量方式。
# max_depth：树的最大深度。
# min_samples_split：节点最小分裂的样本数量。
# max_features：选择特征的数量。
# bootstrap：是否放回抽样。
rf = RandomForestClassifier(n_estimators=100, criterion="gini", random_state=0)
rf.fit(X, y)
print(rf.score(X_train, y_train))
print(rf.score(X_test, y_test))

3.3 bagging回归示例

from sklearn.datasets import load_diabetes
from sklearn.linear_model import LinearRegression
# sklearn提供的用于回归的bagging模型。
# sklearn提供的用于回归的随机深林模型。
from sklearn.ensemble import BaggingRegressor, RandomForestRegressor
from sklearn.model_selection import train_test_split

X, y = load_diabetes(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=0)

lr = LinearRegression()
lr.fit(X_train, y_train)
print("线性回归R ^ 2值：")
print(lr.score(X_train, y_train))
print(lr.score(X_test, y_test))
bag = BaggingRegressor(lr, n_estimators=100, max_samples=0.5, max_features=0.75)
bag.fit(X, y)
print("bagging R ^ 2值：")
print(bag.score(X_train, y_train))
print(bag.score(X_test, y_test))
print("随机森林准确率：")
rf = RandomForestRegressor(n_estimators=100, criterion="mse", random_state=0)
rf.fit(X, y)
print(rf.score(X_train, y_train))
print(rf.score(X_test, y_test))

3.4 结论

从以上两例的运行结果可知，bagging算法可以降低模型的方差，但是，在降低模型偏差方面，作用不大。

4. 随机森林(Random Forest)

随机森林(Random Forest)是一种元评估器，其使用原始数据集的子集来训练多棵决策树，并使用平均方法来计算预测结果。在随机森林中，用于训练决策树的子集样本数量与原始数据集的样本数量是相同的，其实现为：

• 从原始数据集中选出m个样本用于训练（原始数据集的样本数量也为m）。
• 使用这m个样本来构建一棵决策树。
  • 从所有特征中随机选择K个特征（特征不重复）。
  • 根据目标函数的要求（如最大信息增益），使用选定的特征对节点进行划分。
• 重复以上两步n次，即建立n棵决策树。
• 这n棵决策树形成随机森林，通过投票表决结果或均值决定最终的预测值。

关于随机森林，具有如下的说明：

• 用于训练决策树（基本评估器）的数据子集，其样本数量与原始数据集的样本数量相同。
• 默认情况下，随机森林中的决策树在拆分节点时，不再从所有特征中选择最优的特征，而是从随机的特征子集中，选择最优的一个特征。
• 由于这种随机性，随机森林的偏差通常会略微增加（相对于单个非随机决策树的偏差），但由于使用多棵决策树平均预测，其方差也会减小，从而从整体上来讲，模型更加优秀。
• 在分类预测时，scikit-learn中使用概率的平均值进行预测，而不是让每个分类器对单个类别进行投票。
• 对于回归任务，通常设置max_features=n_features，对于分类任务，通常设置max_features=sqrt(n_features)。
• max_depth=None结合min_samples_split=2，通常可以获得很好的结果，但是，这往往会消耗大量的内存。

4.1 随机森林程序(with codes)

将之前bagging的两个示例，去掉注释，查看随机森林模型在分类与回归问题上的效果。

from sklearn.datasets import make_regression
from sklearn.linear_model import LinearRegression
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import train_test_split

X, y = make_regression(n_samples=1000, noise=10, random_state=0, bias=5.5)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
lr = LinearRegression()
lr.fit(X_train, y_train)
print("线性回归结果：")
print(lr.score(X_train, y_train))
print(lr.score(X_test, y_test))
rf = RandomForestRegressor(n_estimators=100, criterion="mse")
rf.fit(X_train, y_train)
print("随机森林结果：")
print(rf.score(X_train, y_train))
print(rf.score(X_test, y_test))

# 葡萄酒数据集
from sklearn.datasets import load_wine
from sklearn.model_selection import train_test_split
from sklearn.ensemble import BaggingClassifier, RandomForestClassifier
from sklearn.tree import DecisionTreeClassifier

X, y = load_wine(return_X_y=True)
# 为了可视化方便，简化操作，我们只取两个特征。
X = X[:, [0, 10]]
# 我们过滤掉0的类别，只取两个类别。
X = X[y != 0]
y = y[y != 0]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=0)

tree = DecisionTreeClassifier(criterion="entropy", max_depth=None)
tree = tree.fit(X_train, y_train)
print("决策树分类准确率：")
print(tree.score(X_train, y_train))
print(tree.score(X_test, y_test))
# n_jobs 开辟进程的数量。如果指定-1，则表示利用现有的所有CPU来实现并行化。
bag = BaggingClassifier(base_estimator=tree, n_estimators=100, max_samples=1.0, max_features=1.0,
        bootstrap=True, bootstrap_features=False, n_jobs=-1, random_state=1)
bag = bag.fit(X_train, y_train)
print("bagging准确率：")
print(bag.score(X_train, y_train))
print(bag.score(X_test, y_test))
rf = RandomForestClassifier(n_estimators=100, criterion="gini", random_state=0, max_depth=None)
rf.fit(X_train, y_train)
print("随机森林准确率：")
print(rf.score(X_train, y_train))
print(rf.score(X_test, y_test))

import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap

mpl.rcParams["font.family"] = "SimHei"
mpl.rcParams["axes.unicode_minus"] = False

cmap = ListedColormap(["r", "g"])
marker = ["o", "v"]
x1_min, x2_min = np.min(X_test, axis=0)
x1_max, x2_max = np.max(X_test, axis=0)
x1 = np.linspace(x1_min - 1, x1_max + 1, 100)
x2 = np.linspace(x2_min - 1, x2_max + 1, 100)
X1, X2 = np.meshgrid(x1, x2)
plt.figure(figsize=(18, 6))
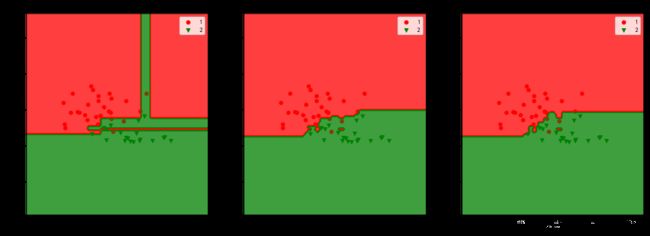
name = ["决策树", "bagging", "随机森林"]
for index, estimator in enumerate([tree, bag, rf], start=1):
    plt.subplot(1, 3, index)
    for i, class_ in enumerate(np.unique(y)):
        Z = estimator.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape)
        plt.contourf(X1, X2, Z, cmap=cmap, alpha=0.5)
        plt.scatter(x=X_test[y_test == class_, 0], y=X_test[y_test == class_, 1], 
                c=cmap(i), label=class_, marker=marker[i])
    plt.title(name[index - 1])
    plt.xlabel("色度")
    plt.ylabel("酒精含量")
    plt.legend()
plt.show()

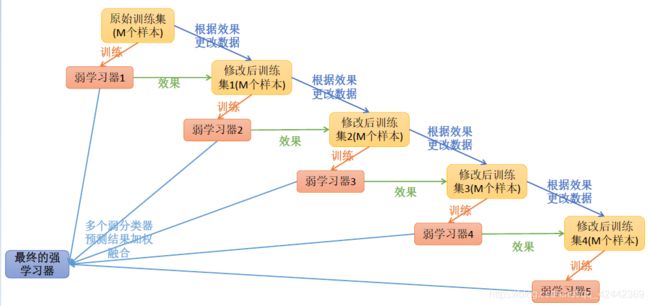
5. boosting

在之前的bagging与随机森林的构建过程中，各个评估器之间没有关系，是相对独立的。例如，在随机森林构建的过程中，构建第m棵子树的时候，不会考虑前面的m-1棵树。
如果在构建过程中，后面的评估器是建立在之前的评估器上的，则就是另外一种集成学习——boosting。
提升学习（Boosting）是一种机器学习技术，可以用于回归和分类的问题，其每一步产生弱预测模型，并加权累加到总模型中。

6. AdaBoost

Adaptive Boosting（AdaBoost）是一种迭代算法。每轮迭代中会在训练集上产生一个新的学习器，然后使用该学习器对所有样本进行预测，以评估每个样本的重要性。
算法会为每个样本赋予一个权重，每次用训练好的学习器标注/预测各个样本，如果某个样本点被预测的越正确，则将其权重降低；否则提高样本的权重。权重越高的样本在下一个迭代训练中所占的比重就越大，也就是说越难区分的样本在训练过程中会变得越重要。整个迭代过程直到错误率足够小或者达到一定的迭代次数为止。

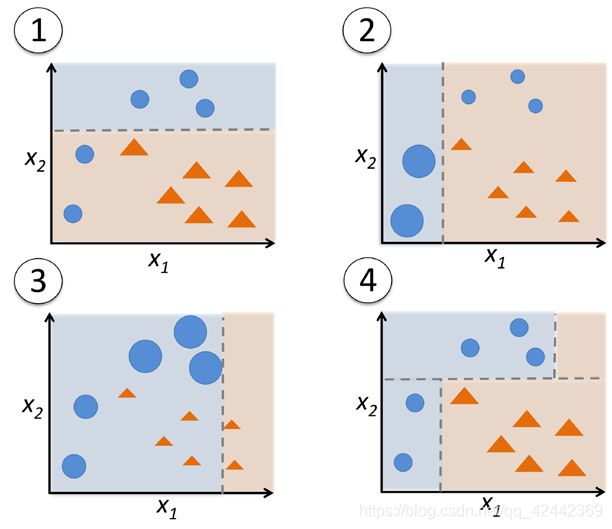
Adaboost算法将基本学习器的线性组合作为强学习器，同时给误差率较小的基本学习器以较大的权重，给误差率较大的基本学习器以较小的权重。构建的线性组合为：
$f(x)={\sum }_{i=1}^m{\alpha }_i{G}_i(x)$
其中，$\alpha$就是每个基本学习器的权重。
对于分类，则在最终的结果上进行sign函数的转换即可：
$G(x)=sign(f(x))=sign({\sum }_{i=1}^m{\alpha }_i{G}_i(x))$

6.1 权重说明

Adaboost算法含有两个权重，一个是样本的权重，一个是评估器（基本的学习器）的权重，不要混淆。

6.2 AdaBoost算法步骤

AdaBoost算法步骤如下（以分类为例）：

1. 初始化每个样本的权重$w$，使得所有样本的权重初始值相同，并且权重和为1。
2. 在第m轮操作中，使用具有权重$w_m$的样本训练基本学习器$G_m(x)$。
3. 使用基本学习器$G_m(x)$预测样本输出值$\hat{y}$。
4. 计算含有权重的错误率：${ϵ}_m=w_m\cdot (y̸=\hat{y})$
5. 计算基本学习器$G_m(x)$的权重系数：${\alpha }_m=0.5\ast log\frac{1-{ϵ}_m}{{ϵ}_m}$
6. 更新权重：$w_m=w_m\ast e^{-{\alpha }_m\ast y\ast \hat{y}}$
7. 对权重$w_m$进行归一化，使其和为1：$w_m=w_j/{\sum }_j{w}_j$
8. 构建基本学习器的线性组合：$f(x) =\sum_{i=1}^{m}\alpha_iG_i(x) $
9. 重复步骤2 ~ 8若干次，获得最终的学习器：$G(x)=sign(f(x))=sign({\sum }_{i=1}^m{\alpha }_i{G}_i(x))$

6.3 AdaBoost示例

假设给定的数据集，如下：

X	0	1	2	3	4	5	6	7	8	9
y	1	1	1	-1	-1	-1	1	1	1	-1

我们假设基本学习器使用决策树，并且不存度衡量标准使用信息熵。

第1轮

在初始状态，所有样本的权值w相同，且和为1。

X	0	1	2	3	4	5	6	7	8	9
y	1	1	1	-1	-1	-1	1	1	1	-1
$w_1$	0.1	0.1	0.1	0.1	0.1	0.1	0.1	0.1	0.1	0.1

训练学习器

分割点可以为2.5、5.5与8.5。
$G_1(x)=\{\begin{array}{cc}1& x<2.5\\ -1& x>2.5\end{array}$

预测输出值

使用训练好的学习器对样本进行预测：

X	0	1	2	3	4	5	6	7	8	9
y	1	1	1	-1	-1	-1	1	1	1	-1
$w_1$	0.1	0.1	0.1	0.1	0.1	0.1	0.1	0.1	0.1	0.1
G1(x)-$\hat{y}$	1	1	1	-1	-1	-1	-1	-1	-1	-1

计算错误率

${ϵ}_1=w_1\cdot (y̸=\hat{y})=0.3$

计算权重系数

${\alpha }_1=0.5\ast log\frac{1-{ϵ}_1}{{ϵ}_1}\approx 0.424$

更新权重

$w_1=w_1\ast e^{-{\alpha }_1\ast y\ast \hat{y}}$
如果预测正确，则$y$与$\hat{y}$符号相同，二者的乘积为正，否则，二者的乘积为负。而$\alpha$的值大于0，因此，预测正确时，权重降低，预测错误时，权重提高。
因此，降低后的权重为：
$0.1\ast e^{-{\alpha }_1}\approx 0.065$
提高后的权重为：
$0.1\ast e^{{\alpha }_1}\approx 0.153$
更新后的结果如下：

X	0	1	2	3	4	5	6	7	8	9
y	1	1	1	-1	-1	-1	1	1	1	-1
$w_1$	0.065	0.065	0.065	0.065	0.065	0.065	0.153	0.153	0.153	0.065
G1(x)-$\hat{y}$	1	1	1	-1	-1	-1	-1	-1	-1	-1

权重归一化

$w_m=w_j/{\sum }_j{w}_j$
${\sum }_j{w}_j=7\ast 0.065+3\ast 0.153=0.914$，因此，归一化的结果为：
预测正确的样本：$0.065/0.914\approx 0.071$
预测错误的样本：$0.153/0.914\approx 0.167$

X	0	1	2	3	4	5	6	7	8	9
y	1	1	1	-1	-1	-1	1	1	1	-1
$w_1$	0.071	0.071	0.071	0.071	0.071	0.071	0.167	0.167	0.167	0.071
G1(x)-$\hat{y}$	1	1	1	-1	-1	-1	-1	-1	-1	-1

线性组合

经过第1轮后，学习器的线性组合为：
$f_1(x)=0.424\ast G_1(x)$

X	0	1	2	3	4	5	6	7	8	9
y	1	1	1	-1	-1	-1	1	1	1	-1
$w_1$	0.071	0.071	0.071	0.071	0.071	0.071	0.167	0.167	0.167	0.071
G1(x)-$\hat{y}$	1	1	1	-1	-1	-1	-1	-1	-1	-1
G-$\hat{y}$	1	1	1	-1	-1	-1	-1	-1	-1	-1

第2轮

在第2轮初始时，数据如下：

X	0	1	2	3	4	5	6	7	8	9
y	1	1	1	-1	-1	-1	1	1	1	-1
$w_2$	0.071	0.071	0.071	0.071	0.071	0.071	0.167	0.167	0.167	0.071

训练学习器

$
prop_1(D_p) = 0.071 * 3 + 0.167 * 3 = 0.714 \
prop_{-1}(D_p) = 1 - 0.714 = 0.286 \
I_H(D_p) = -(0.714 * log_20.714 + 0.286 * log_20.286) = 0.863 \
I_H(D_{x < 2.5}) = 0 \
prop_1((x >=2.5) = (0.167 * 3) / (0.071 * 4 + 0.167 * 3) = 0.638 \
prop_{-1}(x >= 2.5) = 1 - 0.638 = 0.362 \
I_H(D_{x >= 2.5}) = -(0.638 * log_20.638 + 0.362 * log_20.362) = 0.944 \
prop(x < 2.5) = 0.071 * 3 = 0.213 \
prop(x >= 2.5) = 1 - 0.213 = 0.787 \
IG_H(x=2.5) = 0.863 - 0.213 * 0 - 0.787 * 0.944 = 0.120
$

$
I_H(D_{x < 5.5}) = 1 \
prop_1((x >=5.5) = (0.167 * 3) / (0.071 * 1 + 0.167 * 3) = 0.876 \
prop_{-1}(x >= 5.5) = 1 - 0.876 = 0.124 \
I_H(D_{x >= 5.5}) = -(0.876 * log_20.876 + 0.124 * log_20.124) = 0.541 \
prop(x < 5.5) = 0.071 * 6 = 0.426 \
prop(x >= 5.5) = 1 - 0.213 = 0.574 \
IG_H(x=5.5) = 0.863 - 0.426 * 1 - 0.574 * 0.541 = 0.126
$

$
prop_1((x < 8.5) = (0.071 * 3 + 0.167 * 3) / (0.071 * 6 + 0.167 * 3) = 0.770 \
prop_{-1}(x < 8.5) = 1 - 0.770 = 0.230 \
I_H(D_{x < 8.5}) = -(0.770 * log_20.770 + 0.230 * log_20.230) = 0.778 \
I_H(D_{x >= 8.5}) = 0 \
prop(x < 8.5) = 0.071 * 6 + 0.167 * 3 = 0.927 \
prop(x >= 8.5) = 1 - 0.927 = 0.073 \
IG_H(x=8.5) = 0.863 - 0.927 * 0.770 - 0.073 * 0 = 0.149
$
$G_2(x)=\{\begin{array}{cc}1& x<8.5\\ -1& x>8.5\end{array}$

预测输出值

使用训练好的学习器对样本进行预测：

X	0	1	2	3	4	5	6	7	8	9
y	1	1	1	-1	-1	-1	1	1	1	-1
$w_2$	0.071	0.071	0.071	0.071	0.071	0.071	0.167	0.167	0.167	0.071
G2(x)-$\hat{y}$	1	1	1	1	1	1	1	1	1	-1

计算错误率

${ϵ}_2=w_2\cdot (y̸=\hat{y})=0.071\ast 3=0.213$

计算权重系数

${\alpha }_2=0.5\ast log\frac{1-{ϵ}_2}{{ϵ}_2}\approx 0.653$

更新权重

$w_2=w_2\ast e^{-{\alpha }_2\ast y\ast \hat{y}}$
更新后的结果如下：

X	0	1	2	3	4	5	6	7	8	9
y	1	1	1	-1	-1	-1	1	1	1	-1
$w_2$	0.037	0.037	0.037	0.136	0.136	0.136	0.087	0.087	0.087	0.037
G2(x)-$\hat{y}$	1	1	1	1	1	1	1	1	1	-1

权重归一化

$w_m=w_j/{\sum }_j{w}_j$
${\sum }_j{w}_j=0.037\ast 4+0.136\ast 3+0.087\ast 3=0.818$
因此，归一化的结果为：

X	0	1	2	3	4	5	6	7	8	9
y	1	1	1	-1	-1	-1	1	1	1	-1
$w_2$	0.045	0.045	0.045	0.167	0.167	0.167	0.106	0.106	0.106	0.045
G2(x)-$\hat{y}$	1	1	1	1	1	1	1	1	1	-1

线性组合

经过第2轮后，学习器的线性组合为：
$f_2(x)=0.424\ast G_1(x)+0.653\ast G_2(x)$

X	0	1	2	3	4	5	6	7	8	9
y	1	1	1	-1	-1	-1	1	1	1	-1
$w_2$	0.045	0.045	0.045	0.167	0.167	0.167	0.106	0.106	0.106	0.045
G1(x)-$\hat{y}$	1	1	1	-1	-1	-1	-1	-1	-1	-1
G2(x)-$\hat{y}$	1	1	1	1	1	1	1	1	1	-1
G-$\hat{y}$	1	1	1	1	1	1	1	1	1	-1

第3轮

在第3轮初始时，数据如下：

X	0	1	2	3	4	5	6	7	8	9
y	1	1	1	-1	-1	-1	1	1	1	-1
$w_3$	0.045	0.045	0.045	0.167	0.167	0.167	0.106	0.106	0.106	0.045

训练学习器

$prop_1(D_p) = 0.045 * 3 + 0.106 * 3 = 0.453 \
prop_{-1}(D_p) = 1 - 0.453 = 0.547 \
I_H(D_p) = -(0.453 * log_20.453 + 0.547 * log_20.547) = 0.994 \
I_H(D_{x < 2.5}) = 0 \
prop_1((x >=2.5) = (0.106 * 3) / (0.106 * 3 + 0.167 * 3 + 0.045) = 0.368 \
prop_{-1}(x >= 2.5) = 1 - 0.368 = 0.632 \
I_H(D_{x >= 2.5}) = -(0.368 * log_20.368 + 0.632 * log_20.632) = 0.949 \
prop(x < 2.5) = 0.045 * 3 = 0.135 \
prop(x >= 2.5) = 1 - 0.135 = 0.865 \
IG_H(x=2.5) = 0.994 - 0.135 * 0 - 0.865 * 0.949 = 0.173
$

$
prop_1((x < 5.5) = (0.045 * 3) / (0.045 * 3 + 0.167 * 3) = 0.212 \
prop_{-1}(x < 5.5) = 1 - 0.212 = 0.788 \
I_H(D_{x < 5.5}) = -(0.212 * log_20.212 + 0.788 * log_20.788) = 0.745 \
prop_1((x >=5.5) = (0.106 * 3) / (0.106 * 3 + 0.045 * 1) = 0.876 \
prop_{-1}(x >= 5.5) = 1 - 0.876 = 0.124 \
I_H(D_{x >= 5.5}) = -(0.876 * log_20.876 + 0.124 * log_20.124) = 0.541 \
prop(x < 5.5) = 0.045 * 3 + 0.167 * 3 = 0.636 \
prop(x >= 5.5) = 1 - 0.636 = 0.364 \
IG_H(x=5.5) = 0.994 - 0.636 * 0.745 - 0.364 * 0.541 = 0.323
$

$
prop_1((x < 8.5) = (0.045 * 3 + 0.106 * 3) / (0.045 * 3 + 0.106 * 3 + 0.167 * 3) = 0.475 \
prop_{-1}(x < 8.5) = 1 - 0.475 = 0.525 \
I_H(D_{x < 8.5}) = -(0.475 * log_20.475 + 0.525 * log_20.525) = 0.998 \
I_H(D_{x >= 8.5}) = 0 \
prop(x < 8.5) = 0.045 * 3 + 0.106 * 3 + 0.167 * 3 = 0.954 \
prop(x >= 8.5) = 1 - 0.954 = 0.046 \
IG_H(x=8.5) = 0.994 - 0.954 * 0.998 - 0.046 * 0 = 0.042
$
$G_3(x)=\{\begin{array}{cc}1& x<5.5\\ -1& x>5.5\end{array}$

预测输出值

如果按照之前的方式进行预测，则错误率大于0.5，因此，我们按照相反的方式进行预测，即：
$G_3(x)=\{\begin{array}{cc}1& x>5.5\\ -1& x<5.5\end{array}$
使用训练好的学习器对样本进行预测：

X	0	1	2	3	4	5	6	7	8	9
y	1	1	1	-1	-1	-1	1	1	1	-1
$w_3$	0.045	0.045	0.045	0.167	0.167	0.167	0.106	0.106	0.106	0.045
G3(x)-$\hat{y}$	-1	-1	-1	-1	-1	-1	1	1	1	1

计算错误率

${ϵ}_3=w_3\cdot (y̸=\hat{y})=0.045\ast 4=0.180$

计算权重系数

${\alpha }_3=0.5\ast log\frac{1-{ϵ}_3}{{ϵ}_3}\approx 0.758$

更新权重

$w_3=w_3\ast e^{-{\alpha }_3\ast y\ast \hat{y}}$
更新后的结果如下：

X	0	1	2	3	4	5	6	7	8	9
y	1	1	1	-1	-1	-1	1	1	1	-1
$w_3$	0.152	0.152	0.152	0.033	0.033	0.033	0.078	0.078	0.078	0.152
G3(x)-$\hat{y}$	-1	-1	-1	-1	-1	-1	1	1	1	1

权重归一化

$w_m=w_j/{\sum }_j{w}_j$
${\sum }_j{w}_j=0.152\ast 4+0.033\ast 3+0.078\ast 3=0.941$
因此，归一化的结果为：

X	0	1	2	3	4	5	6	7	8	9
y	1	1	1	-1	-1	-1	1	1	1	-1
$w_3$	0.152	0.152	0.152	0.033	0.033	0.033	0.078	0.078	0.078	0.152
G3(x)-$\hat{y}$	-1	-1	-1	-1	-1	-1	1	1	1	1

线性组合

经过第3轮后，学习器的线性组合为：
$f_3(x)=0.424\ast G_1(x)+0.653\ast G_2(x)+0.758\ast G_3(x)$

X	0	1	2	3	4	5	6	7	8	9
y	1	1	1	-1	-1	-1	1	1	1	-1
$w_3$	0.152	0.152	0.152	0.033	0.033	0.033	0.078	0.078	0.078	0.152
G1(x)-$\hat{y}$	1	1	1	-1	-1	-1	-1	-1	-1	-1
G2(x)-$\hat{y}$	1	1	1	1	1	1	1	1	1	-1
G3(x)-$\hat{y}$	-1	-1	-1	-1	-1	-1	1	1	1	1
G-$\hat{y}$	1	1	1	-1	-1	-1	1	1	1	-1

import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeRegressor
# AdaBoostRegressor sklearn中提供的关于AdaBoost回归的模型。
from sklearn.ensemble import AdaBoostRegressor

rng = np.random.RandomState(1)
X = np.linspace(0, 6, 100)[:, np.newaxis]
y = np.sin(X).ravel() + np.sin(6 * X).ravel() + rng.normal(0, 0.1, X.shape[0])


regr_1 = DecisionTreeRegressor(max_depth=4)

regr_2 = AdaBoostRegressor(DecisionTreeRegressor(max_depth=4),
                          n_estimators=50, random_state=rng)
regr_3 = AdaBoostRegressor(DecisionTreeRegressor(max_depth=4),
                          n_estimators=300, random_state=rng)

regr_1.fit(X, y)
regr_2.fit(X, y)
regr_3.fit(X, y)
y_1 = regr_1.predict(X)
y_2 = regr_2.predict(X)
y_3 = regr_3.predict(X)

plt.figure(figsize=(18, 6))
plt.scatter(X, y, c="k", label="训练样本")
plt.plot(X, y_1, c="r", label="n_estimators=1")
plt.plot(X, y_2, c="g", label="n_estimators=50")
plt.plot(X, y_3, c="b", label="n_estimators=300")
plt.xlabel("数据")
plt.ylabel("值")
plt.title("Boosted Decision Tree Regression")
plt.legend()
plt.show()