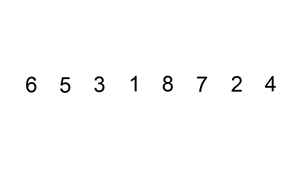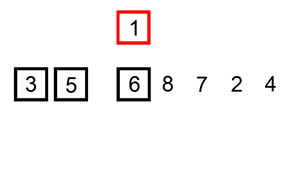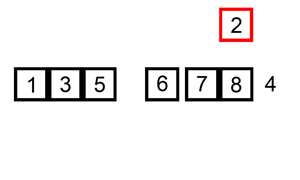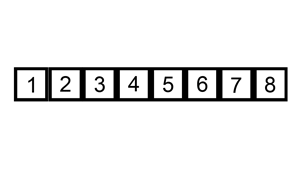基本排序(三):插入排序 和 希尔排序- 从后向前扫描,比正操作元素大的逐步移位
1. 插入排序
插入排序(Insertion Sort)工作原理(维基百科)
通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置插入。插入排序实现上,通常采用in-place排序(即只需用到O(1)的额外空间的排序),因而在从后向前扫描过程中,需要反复把已排序元素逐步向后移位,为最新元素提供插入空间。
- 算法描述:一般来说,插入排序都采用in-place在数组上实现。具体算法描述如下:
- 时间复杂度:
- 最差:O( n2 )
- 最优 : O( n )
- 平均 : O( n2 )
空间复杂度:共O(n),需要辅助空间O(1)
程序实现
void Insertion_sort(Item a[], int l, int r)
{
int i, j;
for(i = l+1; i <= r; i++)
{
Item temp = a[i];
for(j = i-1; j >= l && less(temp, a[j]); j--)
{
a[j+1] = a[j];
}
a[j+1] = temp;
}
}- 总结
和选择排序相比,插入排序的运行时间与输入数据的原始顺序密切相关。例如,如果文件较大,并且关键字已经排好序(或几乎排好序),插入排序比选择排序要快。
2. 希尔排序
希尔排序是基于插入排序的以下两点性质而提出改进方法的:
- 插入排序在对几乎已经排好序的数据操作时,效率高,即可以达到线性排序的效率
- 但插入排序一般来说是低效的,因为插入排序每次只能将数据移动一位(相邻的元素进行交换或移位)
算法原理 From:维基百科
希尔排序通过将比较的全部元素分为几个区域来提升插入排序的性能。这样可以让元素可以一次性地朝最终位置前进一大步。然后再取越来越小的步长进行排序,算法的最后一步就是普通的插入排序(步长为1),但到了这步,需排序的数据几乎是已经排序好的了(此时的插入排序较快)。
例如,假设有这样一组数[ 13 14 94 33 82 25 59 94 65 23 45 27 73 25 39 10 ],如果我们以步长(h)为5开始进行排序,我们可以通过将这列表放在有5列的表中来更好地描述算法,这样他们就应该看起来是这样:
13 14 94 33 82
25 59 94 65 23
45 27 73 25 39
10
移动的增量从1变成了h = 5,然后我们对每列进行排序:
10 14 73 25 23
13 27 94 33 39
25 59 94 65 82
45
将上述四行数字,依序接在一起时我们得到:[ 10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45 ].这时10已经移至正确位置了,然后再以3为步长进行排序:
10 14 73
25 23 13
27 94 33
39 25 59
94 65 82
45
排序之后变为:
10 14 13
25 23 33
27 25 59
39 65 73
45 94 82
94
最后以1步长进行排序(此时就是简单的插入排序了)。
其中步长序列的选择至今没有确定的方法。
程序实现
普通插入排序的C实现:
void Insertion_sort(Item a[], int l, int r)
{
int i, j;
for(i = l+1; i <= r; i++)
{
Item temp = a[i];
for(j = i-1; j >= l && less(temp, a[j]); j--)
{
a[j+1] = a[j];
}
a[j+1] = temp;
}
}那么在希尔排序中只需将步长“1”用“h”替换
void Shell_sort(Item a[], int l, int r)
{
int i, j, h;
for(h = 1; h <= (r-1)/9; h = 3*h+1);//产生步长序列
for(; h > 0; h /= 3)
{
for(i = l+h; i <= r; i = i+h) //步长h
{
Item temp = a[i];
for(j = i-h; j >= l && less(temp, a[j]); j = j-h)
{
a[j+h] = a[j];
}
a[j+h] = temp;
}
}
}希尔排序的较高效率以及代码的简单容易执行,经常被采用。
3. 测试程序
// 插入排序和希尔排序:从后向前扫描,比操作元素大的逐步移位
#include参考资料:
1 插入排序:https://zh.wikipedia.org/wiki/%E6%8F%92%E5%85%A5%E6%8E%92%E5%BA%8F
2 希尔排序:http://zh.wikipedia.org/wiki/%E5%B8%8C%E5%B0%94%E6%8E%92%E5%BA%8F