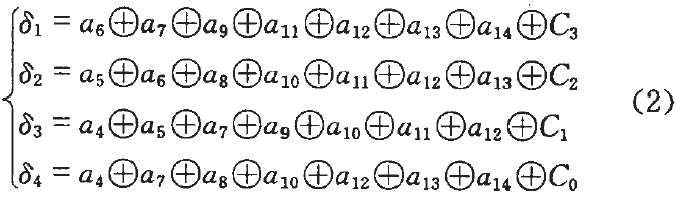4.5 星历(历书)解码
\qquad 在HD-GR导航软件中,负责卫星导航电文处理和星历(历书)解码的分别是电文处理任务(message_task)和星历处理任务(ephemeris_task),它们各自的核心目标是:对于每个保持有效跟踪状态的通道,处理和保存每个完整子帧数据,以及将它们转换为星历(历书)。下面分别讨论HD-GR导航软件解码GPS L1和BDS B1I星历(历书)的一般处理逻辑,包括其中涉及的一些重要技术和算法。
4.5.1 解码GPS L1信号
\qquad 本小节首先讨论解码GPS L1星历(历书)的一般处理逻辑,随后分析导航电文处理过程中所应用的帧同步技术和奇偶校验算法。
1、基本处理
\qquad 一个GPS L1信号通道有待电文处理任务(message_task)来处理,意味着有一位数据(a bit)需要它保存,这一事件促使它调用gps_message.c中的函数gps_process_message(…)相继完成以下处理:
- 将这位数据保存到单字缓冲区[gps_store_bit(…)];
- 如果通道未完成帧同步,查找前导码[gps_look_for_preamble(…)];如果进行了帧同步,复位电文的位计数器;
- 否则(通道已完成帧同步),如果保存的数据位达到30(一个字),对这个字进行奇偶校验并予以保存[gps_store_word(…)],然后将单字计数器加1;进一步,如果保存的单字达到了10,进行以下处理:
- 复位帧同步标志(frame_sync),以重启子帧分析;
- 如果10个单字都有效(一个完整子帧),向星历处理任务(ephemeris_task)发出信号(m_EphemerisChannelFlag),唤醒它将这个子帧转换为星历。
\qquad 一个信号通道有待星历处理任务(ephemeris_task)来处理,意味着它有一个完整子帧需要转换为星历(历书),这一事件促使它调用gps_ephemeris.c中的函数gps_ephemeris_task(…)相继完成以下处理:
- 如果子帧号为1到3,按GPS L1信号ICD定义,将子帧数据转换为星历;
- 如果子帧号为4和5,按GPS L1信号ICD定义,将子帧数据转换为历书;
- 如果子帧1到3完整且有效,将卫星号和星历保存到星历表,设置星历有效标志;
- 清除星历转换过程用到的中间结果,以免星历未完整更新时,重复保存相同结果。
2、帧同步
\qquad 本小节介绍帧同步处理。在此之前,为便于叙述,简介最少量的GPS导航电文知识。
(1) 导航电文
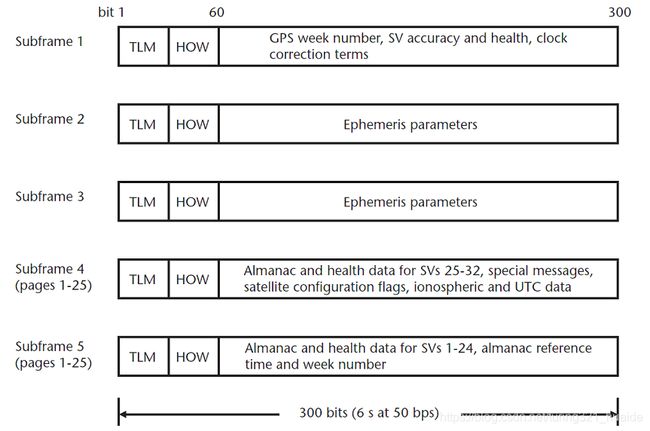
\qquad 如图4-4所示,完整一帧GPS导航电文在5个300-位长的子帧中传输。每个子帧由10个30-位的字组成。导航电文中每个字的最后6-位用于奇偶校验,使用了一种(32, 26)汉明码[(32, 26) Hamming code],以便为用户设备提供在解调时检测错误位的能力。5个子帧从子帧1开始顺序发送。子帧4和5均包含25页,故而在5个子帧的首次循环中,广播子帧4和5的第1页。在5个子帧的下一次循环中,广播子帧4和5的第2页,依次类推。
\qquad 每个子帧的前两个字(1-60位)包含一个遥测字(telemetry, TLM)和一个交接字(handover word, HOW)。TLM是每个子帧的第一个字,MSB先传输。它包括一个固定的前导码(preamble),即一个从不改变的固定8-位图案10001011。这一图案用来辅助用户设备找到每一子帧的起始位置。它还包括仅对授权用户有意义的14-位数据(TLM电文)、以及2个保留位。
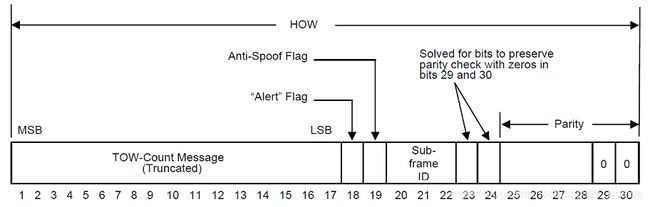
\qquad HOW取名的原因是其提供了以6 s为模的GPS周内时间(time-of-week, TOW),对应于下一子帧起始的边沿,从而允许用户从C/A码跟踪“交接”到P(Y)码跟踪。HOW的格式和内容如图4-5所示,MSB先传输。
- 位1~17为周内时间计数。
- 位18为“报警”标志。位18设置为1表示信号精度可能很差,用户的处理应自担风险。
- 位19为A-S (anti-spoof)标志。位19设置为1指示该SV开启了防欺骗(anti-spoofing)模式。
- 位20~22提供该HOW所在子帧的ID。
- 位23和24的内容是特意设置的,目的是保持校验位的最低两位(D29和D30)总为0。由于校验每个子帧字需用到上一个字的最低两个校验位,因此HOW中这两个总置为0的校验位相当于为相继子帧字的校验赋予了初值。另外,它对成功的子帧同步也很关键,对此后面会进一步说明。
\qquad 关于GPS导航电文的详细描述参见接口控制文档IS-GPS-200D。
(2) 帧同步
\qquad 对于每个保持有效跟踪状态的通道,它的 I I I分支输出数据位。由于GPS数据位速率为50 bps,所以 I I I分支每20 ms 输出一位数据。结合 I I I分支和 Q Q Q分支输出就可得到一个相位输出,即 θ = arctan ( I / Q ) θ = \arctan (I/Q) θ=arctan(I/Q)。假设信号累积时间为1 ms,则每1 ms有一个相位输出。于是实际中就会观察到在连续的20 ms内有连续20 个“相同”的相位输出。不过,由于存在噪声,这20个连续相位并不完全相同,但值都应非常接近于+π/2或-π/2。一旦当前输出相位相比于前一输出相位发生了跳变,则意味数据位发生了变化。另一方面,对于接收机软件而言,它每20 ms记录一个数据位,并将连续数据位保存到本地缓存。软件需要在此本地缓存中搜索子帧前导码,即TLM中的前导码。由于前导码只在8-位长,所以错误搜索概率较大,因此在完成前导码搜索后,还需根据子帧校验逻辑进行子帧完整性检查。只有通过子帧完整性检查,才能对导航电文进行解调。下面对该过理中的有关细节做进一步说明。
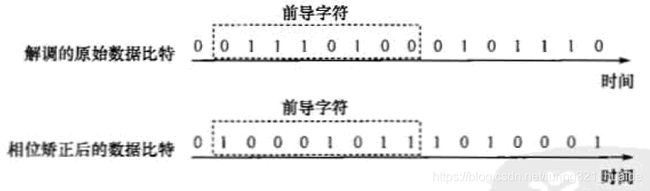
\qquad 由于接收机软件使用Costas环跟踪信号,因此输出的数据位存在0和π的相位模糊。也就是说,如果数据位是0,则I分支输出的位可能是0,也可能是1,于是仅从单个解调的数据位无法得知真实数据位。在软件中,对此问题的解决是在搜索前导码时以一种巧妙的方式同时完成的。我们知道,TLM的8-位前导码为"10001011b",其中后缀b表示二进制。于是解调得到的数据位有两种可能:10001011b或01110100b。第1种结果说明没有0和π的相位模糊,后续数据位无需进行特殊处理。第2种结果说明发生了相位模糊,后续的每个数据位都需进行一次反相操作。图4-6说明了这一点。图中上半部分的数据位是解调得到的原始数据位,可以看出其中包含了一个前导码,但发生了相位模糊;图中下半部分是软件检测到01110100b时,认为发生了相位模糊,将后续的所有数据位都进行了反相处理。
\qquad 检测相位模糊的一种更简单方法是利用HOW校验位的一个重要特性。前面提到过,每个HOW字中第23和第24位的内容是特意设置的,目的是保持校验位的最低两位(D29和D30)总为0,参见图4-5。换句话说,不管HOW字中其它位的内容如何变化,HOW字的最后两个校验位都为0。于是接收机软件可以通过检查前导码之后若干位〈直到HOW最后两个检验位〉的值,如果这两个检验位为0,说明没有发生相位模糊,无需相位反转,否则就需反转。这个特性还可在软件中用来检测搜索到的HOW字是否正确。在实际中,由于存在0和π的相位模糊,所以接收到的D29和D30可能是"11b"或者"00b",而不可能是"01b"或"10b"。如果得到了"01b"或者"10b",说明当前字不是HOW字,需要重新搜索。
\qquad 要说明的是,虽然导航电文每一帧都以前导码开始,但找到了前导码井不说明就找到了一帧的起始,这是因为其它导航电文位也有可能与前导码吻合。前导码只有8-位,所以这种巧合的发生概率不低。更进一步的确定是通过子帧奇偶校验逻辑来实现的。
\qquad 关于帧同步的以上描述参考了“GPS全球定位接收机——原理与软件实现”一书。
3、奇偶校验
\qquad 本小节介绍GPS导航电文应用的奇偶校验技术。首先介绍编码规则,接着介绍一种经典译码算法,最后介绍一种快速译码算法。
(1) 编码规则
\qquad GPS导航电文应用汉明码[(32,26) Hamming Code]进行奇偶校验编码。导航电文的每个子帧包含10个长30-bit的字,其中6-位是编码后加入的奇偶校验位。这些位用于奇偶检查以及校验导航位的极性。如果奇偶校验失败,数据不应该使用。为了进行奇偶校验,要使用8个奇偶校验位。附加的2位是前一个字的最后2位。
\qquad 假设 D i D_i Di代表接收机所接收的一个字的数据位,其中 i = 1 , 2 , 3 , . . . , 24 i = 1, 2, 3, . . . , 24 i=1,2,3,...,24 代表源数据, i = 25 , 26 , . . . , 30 i = 25, 26, . . ., 30 i=25,26,...,30 代表奇偶校验位。奇偶编码方程列在表4.1中,其中: D 29 ∗ D^∗_{29} D29∗和 D 30 ∗ D^∗_{30} D30∗是前一个字的第29和第30个数据;⊕是模2加运算; D 25 D25 D25到 D 30 D30 D30是奇偶校验数据。
\\
\quad 表4.1 奇偶校验编码规则
\qquad 在使用表4.1时,前24个计算必须首先执行,目的是产生一个新数据集 d i , i = 1 d_i, i = 1 di,i=1到 24 24 24。如果 D 30 ∗ = 0 D^∗_{30} = 0 D30∗=0,有 d i = D i d_i = D_i di=Di( i = 1 i = 1 i=1 到 24 24 24),这意味着没有符号变化。如果 D 30 ∗ = 1 D^∗_{30} = 1 D30∗=1,那么由 D i = 0 D_i = 0 Di=0 得 d i = 1 d_i = 1 di=1以及 D i = 1 D_i = 1 Di=1 得 d i = 0 d_i = 0 di=0( i = 1 i = 1 i=1 到 24 24 24)。这个运算改变源数据位的符号。
\qquad 在一台接收机中,导航数据位的极性通常是任意地指派的。列在表4.1中的运算能够自动地校正这种极性。如果 D 30 ∗ = 0 D^∗_{30} = 0 D30∗=0,随后24个数据位的极性不变。如果 D 30 ∗ = 1 D^∗_{30} = 1 D30∗=1,随后24个数据位的极性将改变。这个运算处理位模式的极性。
\qquad 新数据集 d i d_i di用于校验 D 25 D25 D25到 D 30 D30 D30所给出的奇偶关系。在编程实现中,计算表4.1中最后六个方程并不需要对每个方程做多达14次的模2加运算。实际上,只需计数每个方程中值为1的数据位( d i , D 29 ∗ , D 30 ∗ d_i, D^*_{29}, D^∗_{30} di,D29∗,D30∗),如果计数值为奇数, D i = 1 D_i =1 Di=1,否则 D i = 0 D_i =0 Di=0( i = 25 i = 25 i=25 到 30 30 30)。
(2) 经典译码
\qquad 开源GPS之父Clifford Kelley最早编写了(开源的)奇偶校验经典译码算法。前一个字的最后2位( D 29 ∗ , D 30 ∗ D^∗_{29}, D^∗_{30} D29∗,D30∗)和当前字的前30位被打包在一个32-位字(word)中,顺序是( D 29 ∗ , D 30 ∗ , d 1 , d 2 , d 3 , . . . , d 23 , d 24 , D 25 , D 26 , . . . , D 30 D^∗_{29}, D^∗_{30}, d_1, d_2, d_3, ..., d_{23}, d_{24}, D_{25}, D_{26}, ..., D_{30} D29∗,D30∗,d1,d2,d3,...,d23,d24,D25,D26,...,D30),这里的 d i ( i = 1 , … , 24 ) d_i (i =1, …, 24) di(i=1,…,24)为计算出的新数据集,其余为接收机所接收的数据位。对应于表4.1中的最后六个方程,定义以下奇偶位矢量(PB_n)
#define PB_1 0xbb1f3480
#define PB_2 0x5d8f9a40
#define PB_3 0xaec7cd00
#define PB_4 0x5763e680
#define PB_5 0x6bb1f340
#define PB_6 0x8b7a89c0
将32-位字word与PB_n相与(word & PB_n, n = 1, …, 6)就能取出每个方程所感兴趣的每一位。通过计数word & PB_n (n = 1, …, 6)中数据位为1的个数就能得到 D i ( i = 25 , … , 30 ) D_i (i = 25, …, 30) Di(i=25,…,30)的奇偶性。将它们分别与接收的数据位 D i ( i = 25 , … , 30 ) D_i (i = 25, …, 30) Di(i=25,…,30)比较,如果全都相同,则奇偶校验通过,否则奇偶校验失败。
(3) 快速译码
\qquad 本小节的快速译码算法号称是已知算法中最快的,在大部分场合,编译后形成的汇编代码只有30多条指令。快速算法使用预定义常数(幻数)尽可能多地拾取允许结合在一起的数据位,并行地异或(XOR)它们,达到避免冗长的移位和异或循环的目标。
\qquad 下面分析这些常数是如何拾取和异或一个32-位字的数据位的,以及算法是如何产生与表4.1中方程相同的奇偶校验结果的。理解了这些步骤,对开发者最初拆解方程、分组数据位、定义算法常数的思路自然就能领悟了。
1) 32-位常数(幻数)
\qquad 定义以下32-位常数(幻数),其中的代码注释给出了对应的2-进制表示:
#define Mg_0 0xFBFFBF00 // 11111011111111111011111100000000
#define Mg_1 0x07FFBF01 // 00000111111111111011111100000001
#define Mg_2 0xFC0F8100 // 11111100000011111000000100000000
#define Mg_3 0xF81FFE02 // 11111000000111111111111000000010
#define Mg_4 0xFC00000E // 11111100000000000000000000001110
#define Mg_5 0x07F00001 // 00000111111100000000000000000001
#define Mg_6 0x00003000 // 00000000000000000011000000000000
2) 循环左移32-位字
\qquad 将每个打包为( D 29 ∗ , D 30 ∗ , d 1 , d 2 , d 3 , . . . , d 23 , d 24 , D 25 , D 26 , . . . , D 30 D^∗_{29}, D^∗_{30}, d_1, d_2, d_3, ..., d_{23}, d_{24}, D_{25}, D_{26}, ..., D_{30} D29∗,D30∗,d1,d2,d3,...,d23,d24,D25,D26,...,D30)的32-位字(word)进行循环左移Rotation_left(word,n) (n = 0, …, 6),得到以下32-位字:
D*29,D*30,d01,d02,d03,d04,d05,d06,d07, …, d24, P25, P26, …, P30
D*30,d01, d02,d03,d04,d05,d06,d07, …,d24, P25, P26, …, P30, D*29
d01, d02, d03,d04,d05,d06,d07, …,d24,P25, P26, …, P30, D*29,D*30
d02, d03, d04,d05,d06,d07, …,d24,P25,P26, …, P30, D*29,D*30,d01
d03, d04, d05,d06,d07, …,d24,P25,P26, …, P30, D*29,D*30,d01, d02
d04, d05, d06,d07, …,d24,P25,P26, …,P30, D*29,D*30,d01, d02, d03
d05, d06, d07, …,d24,P25,P26, …,P30,D*29,D*30,d01, d02, d03, d04
3) 常数(Mg_n)和字(word)相与
\qquad 将32-位常数Mg_n和循环左移后的32-位字Rotation_left(word,n)相与,结果记为b_n = Rotation_left(word,n) & Mg_n (n = 0, …, 6)。之后,按6列一组排列,可将b_n (n = 0, …, 6)分组为:
组1(列1~6)
D*29 D*30 d01 d02 d03 d04
1 1 1 1 1 0
D*30 d01 d02 d03 d04 d05
0 0 0 0 0 1
d01 d02 d03 d04 d05 d06
1 1 1 1 1 1
d02 d03 d04 d05 d06 d07
1 1 1 1 1 0
d03 d04 d05 d06 d07 d08
1 1 1 1 1 1
d04 d05 d06 d07 d08 d09
0 0 0 0 0 1
d05 d06 d07 d08 d09 d10
0 0 0 0 0 0
组2(列7~12)
d05 d06 d07 d08 d09 d10
1 1 1 1 1 1
d06 d07 d08 d09 d10 d11
1 1 1 1 1 1
d07 d08 d09 d10 d11 d12
0 0 0 0 0 0
d08 d09 d10 d11 d12 d13
0 0 0 0 0 1
d09 d10 d11 d12 d13 d14
0 0 0 0 0 0
d10 d11 d12 d13 d14 d15
1 1 1 1 1 1
d11 d12 d13 d14 d15 d16
0 0 0 0 0 0
组3(列13~18)
d11 d12 d13 d14 d15 d16
1 1 1 1 1 0
d12 d13 d14 d15 d16 d17
1 1 1 1 1 0
d13 d14 d15 d16 d17 d18
1 1 1 1 1 0
d14 d15 d16 d17 d18 d19
1 1 1 1 1 1
d15 d16 d17 d18 d19 d20
0 0 0 0 0 0
d16 d17 d18 d19 d20 d21
0 0 0 0 0 0
d17 d18 d19 d20 d21 d22
0 0 0 0 0 0
组4(列19~24)
d17 d18 d19 d20 d21 d22
1 1 1 1 1 1
d18 d19 d20 d21 d22 d23
1 1 1 1 1 1
d19 d20 d21 d22 d23 d24
0 0 0 0 0 1
d20 d21 d22 d23 d24 P25
1 1 1 1 1 0
d21 d22 d23 d24 P25 P26
0 0 0 0 0 0
d22 d23 d24 P25 P26 P27
0 0 0 0 0 0
d23 d24 P25 P26 P27 P28
1 1 0 0 0 0
不参与最后XOR的2列(列25,26)
d23,d24,
0 0
d24,P25,
0 0
P25,P26,
0 0
P26,P27,
0 0
P27,P28,
0 0
P28,P29,
0 0
P29,P30,
0 0
组5(列27~32)
P25 P26 P27 P28 P29 P30
0 0 0 0 0 0
P26 P27 P28 P29 P30 D*29
0 0 0 0 0 1
P27 P28 P29 P30 D*29 D*30
0 0 0 0 0 0
P28 P29 P30 D*29 D*30 d01
0 0 0 0 1 0
P29 P30 D*29 D*30 d01 d02
0 0 1 1 1 0
P30 D*29 D*30 d01 d02 d03
0 0 0 0 0 1
D*29 D*30 d01 d02 d03 d04
0 0 0 0 0 0
4) 分组合并与奇偶计算
\qquad 将组1到组5按行合并,将(循环左移后的)字的每位与(对应的)常数位相乘,并按列求⊕,可得求解各奇偶校验位 D i ( i = 25 , … , 30 ) D_i (i = 25, …, 30) Di(i=25,…,30)的方程如下:
D25 = D*29*1⊕D*30*0⊕d01*1⊕d02*1⊕d03*1⊕d04*0⊕d05*0⊕
d05*1 ⊕d06*1 ⊕d07*0⊕d08*0⊕d09*0⊕d10*1⊕d11*0⊕
d11*1 ⊕d12*1 ⊕d13*1⊕d14*1⊕d15*0⊕d16*0⊕d17*0⊕
d17*1 ⊕d18*1 ⊕d19*0⊕d20*1⊕d21*0⊕d22*0⊕d23*1⊕
P25*0 ⊕P26*0 ⊕P27*0⊕P28*0⊕P29*0⊕P30*0⊕D*29*0
D26 = D*30*1⊕d01*0⊕d02*1⊕d03*1⊕d04*1⊕d05*0 ⊕d06*0⊕
d06*1 ⊕d07*1⊕d08*0⊕d09*0⊕d10*0⊕d11*1 ⊕d12*0⊕
d12*1 ⊕d13*1⊕d14*1⊕d15*1⊕d16*0⊕d17*0 ⊕d18*0⊕
d18*1 ⊕d19*1⊕d20*0⊕d21*1⊕d22*0⊕d23*0 ⊕d24*1⊕
P26*0 ⊕P27*0⊕P28*0⊕P29*0⊕P30*0⊕D*29*0⊕D*30*0
D27 = d01*1⊕d02*0⊕d03*1⊕d04*1⊕d05*1 ⊕d06*0 ⊕d07*0⊕
d07*1⊕d08*1⊕d09*0⊕d10*0⊕d11*0 ⊕d12*1 ⊕d13*0⊕
d13*1⊕d14*1⊕d15*1⊕d16*1⊕d17*0 ⊕d18*0 ⊕d19*0⊕
d19*1⊕d20*1⊕d21*0⊕d22*1⊕d23*0 ⊕d24*0 ⊕P25*0⊕
P27*0⊕P28*0⊕P29*0⊕P30*0⊕D*29*1⊕D*30*0⊕d01*0
D28 = d02*1⊕d03*0⊕d04*1⊕d05*1 ⊕d06*1 ⊕d07*0⊕d08*0⊕
d08*1⊕d09*1⊕d10*0⊕d11*0 ⊕d12*0 ⊕d13*1⊕d14*0⊕
d14*1⊕d15*1⊕d16*1⊕d17*1 ⊕d18*0 ⊕d19*0⊕d20*0⊕
d20*1⊕d21*1⊕d22*0⊕d23*1 ⊕d24*0 ⊕P25*0⊕P26*0⊕
P28*0⊕P29*0⊕P30*0⊕D*29*0⊕D*30*1⊕d01*0⊕d02*0
D29 = d03*1⊕d04*0⊕d05*1 ⊕d06*1 ⊕d07*1⊕d08*0⊕d09*0⊕
d09*1⊕d10*1⊕d11*0 ⊕d12*0 ⊕d13*0⊕d14*1⊕d15*0⊕
d15*1⊕d16*1⊕d17*1 ⊕d18*1 ⊕d19*0⊕d20*0⊕d21*0⊕
d21*1⊕d22*1⊕d23*0 ⊕d24*1 ⊕P25*0⊕P26*0⊕P27*0⊕
P29*0⊕P30*0⊕D*29*0⊕D*30*1⊕d01*1⊕d02*0⊕d03*0
D30 = d04*0⊕d05*1 ⊕d06*1 ⊕d07*0⊕d08*1⊕d09*1⊕d10*0⊕
d10*1⊕d11*1 ⊕d12*0 ⊕d13*1⊕d14*0⊕d15*1⊕d16*0⊕
d16*0⊕d17*0 ⊕d18*0 ⊕d19*1⊕d20*0⊕d21*0⊕d22*0⊕
d22*1⊕d23*1 ⊕d24*1 ⊕P25*0⊕P26*0⊕P27*0⊕P28*0⊕
P30*0⊕D*29*1⊕D*30*0⊕d01*0⊕d02*0⊕d03*1⊕d04*0
化简后可得以下与IS-GPS-200D中相同的方程:
D25 = D*29⊕d01⊕d02⊕d03⊕d05⊕d06⊕d10⊕d11⊕d12⊕d13⊕d14⊕d17⊕d18⊕d20⊕d23
D26 = D*30⊕d02⊕d03⊕d04⊕d06⊕d07⊕d11d12⊕d13⊕d14⊕d15⊕d18⊕d19⊕d21⊕d24
D27 = d01⊕d03⊕d04⊕d05⊕d07⊕d08⊕d12⊕d13⊕d14⊕d15⊕d16⊕d19⊕d20⊕d22⊕D*29
D28 = d02⊕d04⊕d05⊕d06⊕d08⊕d09⊕d13⊕d14⊕d15⊕d16⊕d17⊕d20⊕d21⊕d23⊕D*30
D29 = d03⊕d05⊕d06⊕d07⊕d09⊕d10⊕d14⊕d15⊕d16⊕d17⊕d18⊕d21⊕d22⊕d24⊕D*30⊕d01
D30 = d05⊕d06⊕d08⊕d09⊕d10⊕d11⊕d13⊕d15⊕d19⊕d22⊕d23⊕d24⊕D*29⊕d03
5) 代码参考
\qquad 以下快速译码代码复制自开源GPS网站https://github.com/gps-sdr,列在这里,仅作学习的参考。
// https://github.com/gps-sdr/gps-sdr/blob/master/objects/channel.cpp
bool Channel::ParityCheck(uint32 gpsword)
{
uint32 d1,d2,d3,d4,d5,d6,d7,t,parity;
/* XOR as many bits in parallel as possible. The magic constants pick
up bits which are to be XOR'ed together to implement the GPS parity
check algorithm described in ICD-GPS-200. This avoids lengthy shift-
and-xor loops. */
d1 = gpsword & 0xFBFFBF00;
d2 = _lrotl(gpsword,1) & 0x07FFBF01;
d3 = _lrotl(gpsword,2) & 0xFC0F8100;
d4 = _lrotl(gpsword,3) & 0xF81FFE02;
d5 = _lrotl(gpsword,4) & 0xFC00000E;
d6 = _lrotl(gpsword,5) & 0x07F00001;
d7 = _lrotl(gpsword,6) & 0x00003000;
t = d1 ^ d2 ^ d3 ^ d4 ^ d5 ^ d6 ^ d7;
// Now XOR the 5 6-bit fields together to produce the 6-bit final result.
parity = t ^ _lrotl(t,6) ^ _lrotl(t,12) ^ _lrotl(t,18) ^ _lrotl(t,24);
parity = parity & 0x3F;
if (parity == (gpsword&0x3F))
return(true);
else
return(false);
}
4.5.2 解码BDS B1I信号
\qquad 本小节首先讨论解码BDS B1I星历(历书)的一般处理逻辑,随后分析导航电文处理过程中所应用的帧同步技术及纠错、校验技术。
1、基本处理
\qquad 一个BDS B1I信号通道有待电文处理任务(message_task)来处理,意味着它有一位数据(a bit)需要保存,这一事件促使message_task调用位于b1i_message.c中的函数b1i_process_message(…)相继完成以下处理逻辑:
- 如果通道未完成帧同步,进行帧同步[b1i_sync_frame(…)]。如果这时完成了帧同步,复位电文的位计数器;
- 否则(通道已完成帧同步),首先对经过二次编码的数据位进行译码,结果保存到单字缓冲区[b1i_store_bit (…)];如果保存的数据位达到30(一个字),对这个字进行纠错、校验并保存[b1i_store_word(…)],然后将单字计数器加1;进一步,如果保存的单字数达到了10个,进行以下处理:
- 为重启子帧分析复位帧同步标志(frame_sync);
- 如果10个单字都有效(一个完整子帧),向星历处理任务(ephemeris_task)发出信号(m_EphemerisChannelFlag),唤醒它将这个子帧数据转换为星历。
\qquad 一个信号通道有待星历处理任务(ephemeris_task)来处理,意味它有一个完整子帧需要转换为星历(历书),这一事件促使ephemeris_task调用位于b1i_ephemeris.c中的函数b1i_ephemeris_task(…)相继完成以下处理逻辑:
- 如果导航电文为D1类型(根据卫星PRN号判断):
- 如果子帧号为1到3,按BDS B1I信号ICD定义,将子帧数据转换为星历;
- 如果子帧号为4和5,按BDS B1I信号ICD定义,将子帧数据转换为历书;
- 如果子帧1到3完整且有效,将卫星号和星历保存到星历表中,设置星历有效标志;
- 清除星历转换过程用到的中间结果,以免星历未完整更新时,重复保存相同结果。
- 否则(导航电文为D2类型),如果子帧号为1:
- 获取页号(page number)。如果页号为1到10,按BDS B1I信号ICD定义,将子帧数据转换为星历;
- 如果子帧1完整且有效,将卫星号和星历保存到星历表中,设置星历有效标志;
- 清除星历转换过程用到的中间结果,以免星历未完整更新时,重复保存相同结果。
2、帧同步
\qquad BDS B1I导航电文有两种类型:D1电文和D2电文,数据位传输速率分别为20 ms和2 ms。帧同步就是要将20 ms或2 ms的数据位流与电文中的子帧同步码(前导码,子帧第一个字的第1~11位)或其反转值进行匹配,再按BDS ICD的规定,对数据位进行纠错和校验 ,从而找到正确的子帧头位置。这一过程与GPS L1信号C/A码导航电文的子帧同步类似,实际上相对简单些,因此不再重复。
\qquad 关于BDS B1I导航电文的介绍,参见“北斗卫星导航系统空间信号ICD(公开服务信号2.0版)”。
3、纠错和校验
(1) 纠错编码
\qquad 尽管BDS B1I有两种导航电文类型,但无论哪种类型,子帧中的每个字都由导航电文数据及校验码两部分组成。每个子帧第1 个字的前15-位信息不进行纠错编码,后11-位信息采用BCH(15,11,1) 方式进行纠错,信息位共有26-位;其余9个字均采用BCH(15,11,1)加交织方式进行纠错编码,信息位共有22-位。
\qquad BCH(15,11,1)码长15-位,数据位为11-位,纠错能力为1-位,生成多项式为:
g ( x ) = x 4 + x + 1 g(x) = x^4 + x + 1 g(x)=x4+x+1
导航电文数据码按每11-位顺序分组,对需要交织的数据进行串/并变换,然后进行BCH(15, 11,1)纠错编码。每两组BCH(15,11,1)码按比特交错方式组成30-位码长的交织码,30-位码长的交织码编码结构为:
![]()
其中: X i j X_i^j Xij为信息位, i i i 表示第 i i i 组BCH 码,其值为1 或2; j j j表示第 i i i组BCH 码中的第 j j j个信息位,其值为1~11; P i m P_i ^ m Pim为校验位, i i i表示第 i i i组BCH码,其值为1 或2; m m m 表示第 i i i组BCH 码中的第 m m m个校验位,其值为1~4。
(2) 纠错译码
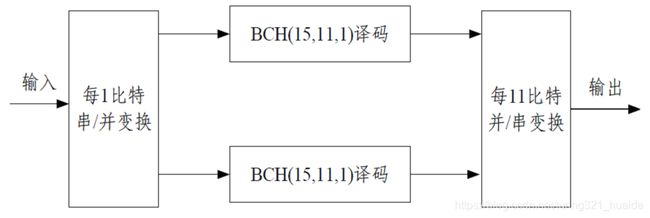
\qquad 根据编码规则,纠错译码分3 个步骤完成:(1)首先对接收到的导航电文码进行“每1-位串/并转换”;(2)将30-位导航电文分成两组BCH码,分别进行纠错译码;(3)最后将得到的两组15-位的纠错码进行“每1-位并/串转换”。如图4-7所示。
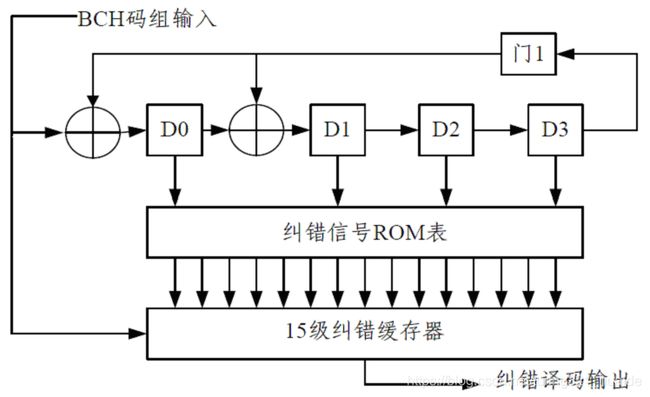
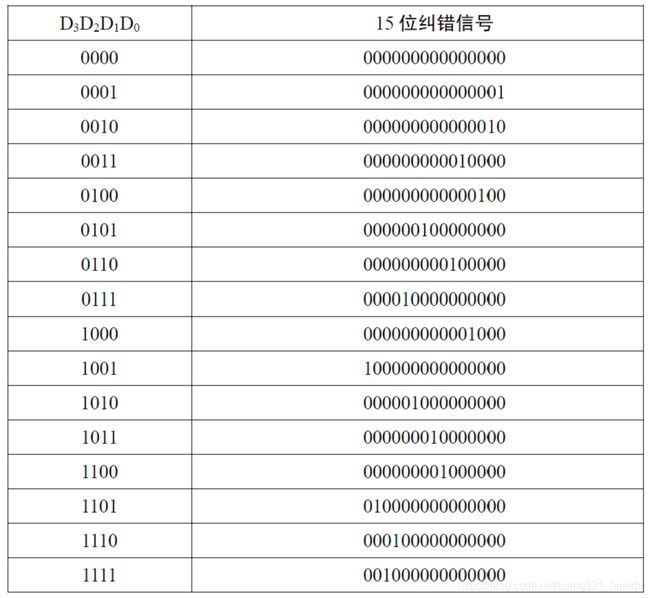
\qquad BCH(15,11,1)译码框图见图4-8,其中,初始时移位寄存器清零。BCH 码组逐位输入到除法电路和15 级纠错缓存器中,当BCH 码的15 位全部输入后,利用除法电路的4 级移位寄存器的状态 D 3 、 D 2 、 D 1 、 D 0 D_3、D_2、D_1、D_0 D3、D2、D1、D0查找纠错信号ROM 表,得到15 位纠错信号与15 级纠错缓存器里的值模二加,最后输出纠错后的信息码组。纠错信号的ROM表见表4-2。
\\
\quad 表4-2 纠错信号的ROM 表
 \qquad 下面解释一下表4-2的由来,详细参见“北斗2代B1I信号导航电文分析”一文 。由(1)中所述的编码过程可以得到以下监督方程组:
\qquad 下面解释一下表4-2的由来,详细参见“北斗2代B1I信号导航电文分析”一文 。由(1)中所述的编码过程可以得到以下监督方程组:
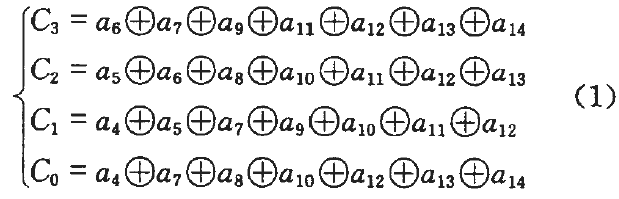
其中: a 4 , … , a 14 a_4, …, a_{14} a4,…,a14为11个信息码元; C 0 , … , C 3 C_0, …, C_3 C0,…,C3为与生成多项式所产生的4个校验位相对应的4个校验位监督码元。
\qquad 通过这个监督方程组,监督码元对信息码元实行监督,使原来完全独立的信息码元被约束到了这种联系当中。当码元在传输过程中发生差错时,方程组中与这些码元相应的方程式被破坏。因此,接收端很容易通过监督方程组来发现错误,而且由于信息码元受到多个监督码元的多重监督,不仅能发现错误,还能纠正错误。
\qquad 将监督方程组改写成误差方程组的形式:
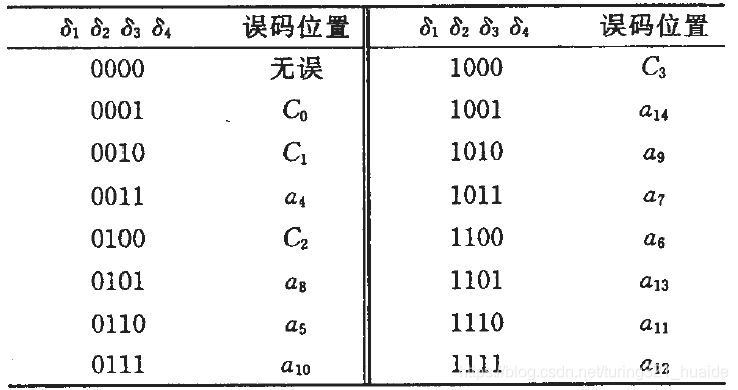
\qquad 如果接收的码组没有错误,则(2)式 δ i = 0 ( i = 1 , 2 , 3 , 4 ) δ_i = 0 (i=1,2,3,4) δi=0(i=1,2,3,4)。由于BCH(15, 11, 1)编码只能进行1位纠错,所以如果码组中发生单个错误,按以下两种方法进行纠错:1)当只有某一个 δ i ≠ 0 δ_i ≠ 0 δi=0时,若该 δ i δ_i δi所在的误差方程中的某个码元没有出现在其它3个误差方程中,则该码元即为误码位置;2)当有多个 δ i ≠ 0 δ_i ≠ 0 δi=0时,若某个码元同时出现在这几个 δ i δ_i δi所在的误差方程中,则该码元即为误码位置。这样,接收端便可根据 δ i δ_i δi的不同值唯一地确定误码的位置,计算结果如表4-3所示。所以若知道了错误的位置,只要将收到的该位码元变号,将1变为0,或0变为1,就纠正了错误。比较表4-2和表4-3,知道它们完全相同。
(3) 译码校验
\qquad 在原始导航电文码中注入纠错编码是在卫星上进行的,该导航电文在通过传输通道到达用户接收机时,出现误码的概率是有的。而且由于BCH(15, 11, 1)纠错码只能对1-位误码情况进行纠正,若某个字的导航电文在传输的过程中发生了超过1-位的误码,则该系统无法得到正确判断,这样将会给系统造成严重后果。所以,对纠错解码后的电文进行校验是必须的工作。校验可按以下步骤进行:
- 从30-位导航电文字(含校验码)中取出高22 位,即导航电文数据,并将其分成两组,每组11-位;然后取出低8-位即校验码。
- 按照BCH (15, 11, 1)编码过程,分别计算出2 组电文的4-位校验位。
- 用步骤1中取出的8-位校验码与步骤2中计算出来的8-位校验码比较,如果相同,说明数据正确,否则说明电文在传输或基带处理的过程中出现了误码。误码可能是电文误码, 也可能是检验字误码。