1.常用排序算法总结
序
常见的排序算法有8种:
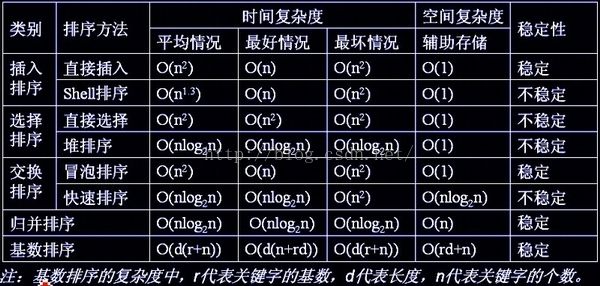
表格:
| 排序方法 | 时间复杂度(平均) | 时间复杂度(最坏) | 时间复杂度(最好) | 空间复杂度 | 稳定性 |
|---|---|---|---|---|---|
| 冒泡排序 | O(n2) | O(n2) | O(n) | O(1) | 稳定 |
| 直接选择排序 | O(n2) | O(n2) | O(n2) | O(1) | 不稳定 |
| 直接插入排序 | O(n2) | O(n2) | O(n) | O(1) | 稳定 |
| 希尔排序 | O(nlog2n) | O(n2) | O(n) | O(1) | 不稳定 |
| 堆排序 | O(nlog2n) | O(nlog2n) | O(nlog2n) | O(1) | 不稳定 |
| 快速排序 | O(nlog2n) | O(n2) | O(nlog2n) | O(nlog2n) | 不稳定 |
| 归并排序 | O(nlog2n) | O(nlog2n) | O(nlog2n) | O(n) | 稳定 |
| 基数排序 | O(d(n+r)) | O(d(n+r)) | O(d(n+r)) | O(n+r) | 稳定 |
图片为转载,如侵删:
冒泡排序和选择排序用的不是很多,因为时间复杂度高,但是因为常数项少,小规模排序执行时间不一定比其他排序长。
插入排序 虽然时间复杂度高,但是因为常数项比较小,通常用在大致排序完成后最后的调整阶段。比如Java中Array.sort()的底层实现便用了二分插入排序(长度小于32的Tim sort算法)。
快速排序和归并排序是最常用的。堆排序的思想比较重要,涉及到优先队列的问题。
基数排序 能够解决一些特定的问题。
下面排序都会用到的辅助代码:
//交换位置
public static void swap(int[] arr, int i, int j) {
/* 不能用于浮点数和交换自身
arr[i] = arr[i] ^ arr[j];
arr[j] = arr[i] ^ arr[j];
arr[i] = arr[i] ^ arr[j];
*/
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}1. Bubble Sort(冒泡排序)
过程:
1. 从0位置开始,比较相邻两个数的大小,如果后面的数小于前面,则交换位置。
2. 遍历一遍下来,最后一个数为整个数组中的最大值。
3. 把最后一个数排除,继续比较剩下的数组。
4. 总共比较次数为N*N,时间复杂度为O(n²)。
//Bubble Sort
public static void bubbleSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
for (int i = arr.length - 1; i > 0; i--) {
for (int j = 0; j < i; j++) {
if (arr[j] > arr[j + 1]) {
swap(arr, j, j + 1);
}
}
}
}
2. Selection Sort (选择排序)
过程:
- 遍历一遍,找到整个数组中最小的数,与位置0的数交换位置。
- 从1位置开始,继续遍历,找到最小的数,与1位置交换。以此类推。
- 同冒泡排序,复杂度为O(n²)。
//Selection Sort
public static void selectionSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
for (int i = 0; i < arr.length - 1; i++) {
int minIndex = i;
for (int j = i + 1; j < arr.length; j++) {
minIndex = arr[j] < arr[minIndex] ? j : minIndex;
}
swap(arr, i, minIndex);
}
}
3. Insertion Sort(插入排序)
过程:
- 从1位置开始,比较与前面数的大小,如果小于前面的数,则交换位置,直到不再小于停止。
- 接着从2位置开始,重复这个过程。直到最后位置为止。
- 时间复杂度取决于数组的排序情况,当数组基本有序时候,复杂度很低,接近O(n)。当数组完全无序时,每个数都要经过多次移动,复杂度趋近于O(n²)。
//Insertion Sort
public static void insertionSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
for (int i = 1; i < arr.length; i++) {
for (int j = i - 1; j >= 0 && arr[j] > arr[j + 1]; j--) {
swap(arr, j, j + 1);
}
}
}
4. Shell Sort(希尔排序)
过程:
1. 过程类似于插入排序,算是插入排序的一种优化。
2. 首先,需要确定一个步长k,根据步长,把数组分为N/k部分,每一部分单独排序。
3. 把步长缩短,继续排序,直到步长为1。
4. 通过步长,减少了数组需要移动的次数,从而降低了复杂度。
5. 所以复杂度的高低完全取决于步长的好坏,是一种特别不稳定的算法,也是一种实现简单分析困难的算法。
//维基上找的,没自己写
# Sort an array a[0...n-1].
gaps = [701, 301, 132, 57, 23, 10, 4, 1]
# Start with the largest gap and work down to a gap of 1
foreach (gap in gaps)
{
# Do a gapped insertion sort for this gap size.
# The first gap elements a[0..gap-1] are already in gapped order
# keep adding one more element until the entire array is gap sorted
for (i = gap; i < n; i += 1)
{
# add a[i] to the elements that have been gap sorted
# save a[i] in temp and make a hole at position i
temp = a[i]
# shift earlier gap-sorted elements up until the correct location for a[i] is found
for (j = i; j >= gap and a[j - gap] > temp; j -= gap)
{
a[j] = a[j - gap]
}
# put temp (the original a[i]) in its correct location
a[j] = temp
}
}5. Quick Sort(快速排序)
需要重点掌握:
- 快速排序是一种很重要也很常用的排序,也有一些很重要的应用,比如说BFPRT算法,荷兰国旗问题。
- 快速排序如果每次都选到最大值,或者最小值,就会产生最坏的情况,使复杂度达到O(n²)级别。但是可以通过随机选择partition值,从数学期望上避免这种情况的发生。所以可以默认其复杂度为O(N * lg N)。
- 一般默认快速排序是非稳定的。但是有论文级别的方法,可以使其实现稳定(0-1 stable sort)。看看就好。。。
过程:
- 随机选出一个partition值,把大于partition值的放在它右边,小于它的放在它左边。
- 从partition值的左右两边分割,调用自己,开始递归。
- 这里有一点优化,因为partition值在数组中可能不止一个,因此返回一个长度为2的数组,代表partition的左右边界,从边界两端进行递归,更加快速。
public static void quickSort(int[] arr) {
if ( arr == null || arr.length < 2) {
return;
}
quickSort(arr, 0, arr.length-1);
}
public static void quickSort(int[] arr, int left, int right) {
if ( left >= right ) {
return;
}
//随机产生partition值,防止出现最坏情况
swap(arr, right, (int) (Math.random() * ( right - left + 1) )+ left );
//返回的数组p为partition的左右边界
int[] p = partition(arr, left, right);
quickSort(arr, left, p[0]-1);
quickSort(arr, p[1]+1, right);
}
public static int[] partition(int[] arr, int left, int right) {
int less = left - 1, more = right;
while ( left < more ) {
if ( arr[left] < arr[right] ) {
swap(arr, ++less, left++);
} else if ( arr[left] > arr[right] ) {
swap(arr, --more, left);
} else {
left++;
}
}
swap(arr, more, right);
return new int[] {less+1,more};
}
6. Merge Sort(归并排序)
需要重点掌握:
- 归并排序的优势很明显,它是稳定排序。同时相对于快排,它占用较多的空间。
- 递归的思想很重要,分治法的应用也很广泛,把大问题分解成小问题一步步解决。
- 递归过程要掌握,递归过程一定要有一个终止条件。
- 压栈的过程,空间的占用要理解。
- 同样有论文级别的算法可以把归并排序的空间省下来,知道就好。ORZ。。。 默认空间复杂度 O(n)。
过程:
- 把数组分成两部分,分别比较大小,最后合并。
- 递归调用自己。
public static void mergeSort(int[] arr) {
if ( arr == null || arr.length < 2 ) {
return;
}
mergeSort(arr, 0, arr.length - 1 ) ;
}
public static void mergeSort(int[] arr, int l, int r) {
if (l == r) {
return;
}
int mid = l + ((r - l) >> 1);
mergeSort(arr, l, mid);
mergeSort(arr, mid + 1, r);
merge(arr, l, mid, r);
}
public static void merge(int[] arr, int l, int m, int r) {
int[] help = new int[r - l + 1];
int i = 0;
int p1 = l;
int p2 = m + 1;
while (p1 <= m && p2 <= r) {
help[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];
}
while (p1 <= m) {
help[i++] = arr[p1++];
}
while (p2 <= r) {
help[i++] = arr[p2++];
}
for (i = 0; i < help.length; i++) {
arr[l + i] = help[i];
}
}7. Heap Sort(堆排序)
重点:
- 堆排序是一种复杂度很稳定的算法,没有最差或者最好,稳定的 n * lg N。
- 堆排序可以拓展到优先队列的实现,在贪心算法中经常用到。
过程:
- 首先用数组构造一个大根堆。
- 把大根堆队顶和最后位置的元素交换位置,最后一个元素脱离大根堆,即数组长度减一。
- 队顶下沉,再次构造大根堆,重复这个过程,直至完全排序。
public static void HeapSort(int[] arr) {
if ( arr == null || arr.length < 2 ) {
return;
}
for ( int i = 1; i < arr.length; i++ ) {
insertHeap(arr, i);
}
int r = arr.length - 1;
while(r > 0 ) {
swap(arr, 0, r);
heapify(arr, 0, r--);
}
}
public static void insertHeap(int[] arr, int i) {
while (arr[i] > arr[(i - 1) / 2]) {
swap(arr, i, (i - 1) / 2);
i = (i - 1) / 2;
}
}
public static void heapify(int[] arr, int index, int size) {
int left = index * 2 + 1;
while ( left < size ) {
int largest = left+1 < size && arr[left] < arr[left + 1] ? left+1 : left;
if ( arr[index] > arr[largest] ) {
return;
}
swap(arr, index, largest);
index = largest;
left = index * 2 + 1;
}
}
8. Radix Sort / Count Sort(基数排序 / 计数排序)
- 桶排序(Bucket Sort)属于非比较排序,因此适用范围很窄,但是在特定问题上可以把时间复杂度做到 O(n)。
- 桶排序只是一个概念,一种非比较排序的思想。基数排序和计数排序都算桶排序的一种落地(实现)。
计数排序(Count Sort)
适用范围:
- 计数排序适用于明确范围的数字排序
过程:
- 找的数组最大值max,new出来max+1个桶。
- 遍历整个数组,把数组里的数全部扔到对应的桶里。
- 从第一个桶开始遍历所有桶,把遍历的值填充到原来的数组中。
其他:
- 计算排序其实可以优化,但这个瓶颈会一直存在。即必须为一定范围内的数组集合。
代码:
// only for 0~200 value
public static void bucketSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
int max = Integer.MIN_VALUE;
for (int i = 0; i < arr.length; i++) {
max = Math.max(max, arr[i]);
}
int[] bucket = new int[max + 1];
for (int i = 0; i < arr.length; i++) {
bucket[arr[i]]++;
}
int i = 0;
for (int j = 0; j < bucket.length; j++) {
while (bucket[j]-- > 0) {
arr[i++] = j;
}
}
}基数排序(Radix Sort)
过程:
- 首先需要理解一点:当个位排好顺序时,再对十位开始排序时,个位的相对位置不变。
- 什么叫相对位置?比如对23,26,58,93进行排序,个位排好后是23,93,26,58。
- 这时再对十位进行排序,23,26的相对位置是不会变的,排序结束为23,26,58,93。
- 这个思维过程有点像动态规划,把问题分为n个小步骤,每个下一步都会用到上一步的结果。
代码:
// only for no-negative value
public static void radixSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
radixSort(arr, 0, arr.length - 1, maxbits(arr));
}
public static int maxbits(int[] arr) {
int max = Integer.MIN_VALUE;
for (int i = 0; i < arr.length; i++) {
max = Math.max(max, arr[i]);
}
int res = 0;
while (max != 0) {
res++;
max /= 10;
}
return res;
}
public static void radixSort(int[] arr, int begin, int end, int digit) {
final int radix = 10;
int i = 0, j = 0;
int[] count = new int[radix];
int[] bucket = new int[end - begin + 1];
for (int d = 1; d <= digit; d++) {
for (i = 0; i < radix; i++) {
count[i] = 0;
}
for (i = begin; i <= end; i++) {
j = getDigit(arr[i], d);
count[j]++;
}
for (i = 1; i < radix; i++) {
count[i] = count[i] + count[i - 1];
}
for (i = end; i >= begin; i--) {
j = getDigit(arr[i], d);
bucket[count[j] - 1] = arr[i];
count[j]--;
}
for (i = begin, j = 0; i <= end; i++, j++) {
arr[i] = bucket[j];
}
}
}
public static int getDigit(int x, int d) {
return ((x / ((int) Math.pow(10, d - 1))) % 10);
}