Actor-Attention-Critic for Multi-Agent Reinforcement Learning论文学习笔记

论文链接：Actor-Attention-Critic for Multi-Agent Reinforcement Learning

    最近学习了ICML2019的一篇多智能体强化学习的文章，感觉想法很新颖，所以记录一下学习时候的笔记，方便以后查阅。文中有不恰当或者有问题的地方，欢迎在评论区批评指正。

一.改进算法的核心内容

     改进的算法主要是结合COMA算法中的“反事实基线”的思想，用于解决“信用分配”（Credit Assignment）问题，即如何分配奖励进而鼓励那些对整个多智能体任务更有帮助的单智能体，进而促进他们更好地学习优秀的策略。此外，在actor网络以及critic网络中引入soft actor-critic算法（以下简称SAC算法）思想中的交叉熵的概念，促进智能体在进行探索的时候，能够更有效地利用周围的信息进行学习。最为重要的改进，也就是这个算法的核心思想，通过借鉴深度学习领域中的“Attention”机制，来实现如何抓住智能体交互中最有效的信息进行学习，进而可以提高智能体的学习效率和策略的稳定性。这个算法的改进是建立在Actor-Critic框架的基础上的，通过利用集中式的训练，来解决多智能体环境中动态马尔可夫环境的问题；以及每个智能体分散式地执行各自的动作，来解决多智能体环境中联合动作空间随着智能体数量的增长，呈现指数爆炸维度过高的问题。

i.Attention机制

    Attention 机制是整个算法的核心，它引入的目的是希望智能体在学习其他智能体策略的时候，能够有选择性的关注更有利于自己获取更大回报的信息进行学习，而不像MADDPG算法那样，无差别的完全学习其他智能体的所有信息。直观地理解，Attention机制本质上是让每个智能体能够查询到其他智能体的观测信息和动作信息，并将这些信息通过重要性的大小整合到自己的动作值函数估计中。当然，Attention机制的应用也不同于深度学习中自然语言处理和计算机视觉那样，其并不需要对时间和空间位置做出假设，这样使得算法能够更加灵活地应用到多智能体的环境中去。
    为了更好的引入Attention机制，需要对动作值函数$Q_i^{\psi }$进行改进。首先，定义critic网络的输入是所有智能体的观测信息$o=(o_1,\cdots ,o_N)$和动作信息$a=(a_1,\cdots ,a_N)$,并定义所有智能体的索引i∈{1⋯N}。并且为了后面对COMA算法思想的引入，这里还需要定义除去智能体i的集合为\i，并且索引集合用j来表示，这样$Q_i^{\psi }$定位为：
$$Q_i^{\psi }(o,a)=f_i(g_i(o_i,a_i),x_i)$$
    其中$f_i$是一个双层MLP网络，而$g_i$是一个单层MLP嵌入式网络函数。$x_i$是其他智能体对该智能体所得奖励的贡献大小的加权和，定义为：
$$x_i=\sum _{(j\ne i)}{\alpha }_j{v}_j=\sum _{(j\ne i)}{\alpha }_{j}h(V{g}_j(o_j,a_j))$$
    其中，$v_j$是智能体j的嵌入式编码函数$e_j=g_j(o_j,a_j)$通过一个线性的共享矩阵V变换，再由一个元素之间的非线性变换函数h处理得到。
    Attention权重${\alpha }_j$是通过使用双线性映射，即查询值-键值系统，比较$e_j$与$e_i=g_i(o_i,a_i)$,并将二者的相似值传递给softmax网络处理得到：
$${\alpha }_j\propto exp(e_j^T{W}_k^T{W}_q{e}_i)$$
    其中，$W_q$将$e_i$转化为查询值，$W_k$将$e_j$转化成键值，然后根据这两个矩阵的维数进行匹配，以防止梯度消失。在实验设计中，算法使用了多Attention heads。每一个head，使用一套独立的参数$(W_k,W_q,V)$，这就是其他智能体对智能体i的联合贡献，并且每一个head都能实现从不同角度关注其他智能体的权重贡献和。
    另外，智能体的特征提取器，键和值都是在多智能体之间共享的，这使得经过网络处理变换以后，所有智能体的特征处在同一个空间。在不同的智能体之间共享参数无论在合作环境还是竞争环境下，都是是可行的。这是因为多智能体系统中的动作值函数的近似问题本质上就是一个多目标回归问题。这种参数共享机制在每个智能体获得不同奖励，但是共享特征空间的环境下，能够使智能体有效的学习。下图为Attention机制的流程图：

    整个流程如上图所示，当智能体i将自己的$(o_i,a_i)$传入MLP网络中得到编码$e_i$,并将其传入Attention Mechanism中，得到权重$x_i$传给另一个MLP值函数网络，得到对应的动作值函数$Q_i(o,a)$。下面是Attention Mechanism内部的一个处理流程图：

    上图中，每个智能体通过编码函数都可以编码成e,每一个e通过不同网络的处理，得到Query、key以及value。对于智能体i来说，将自己的Query以及其他智能体的key处理得到Attend Weight,并与其他智能体的Value结合，得到其他智能体对智能体i的贡献加权和。

ii.反事实基线

    反事实基线的思想最早来源于COMA算法，该思想主要是通过优势函数，来解决多智能体环境中“信用”分配问题，即如何分配奖励进而鼓励那些对整个多智能体任务更有帮助的单智能体，进而促进他们更好地学习优秀的策略。反事实基线的核心思想：评价一个智能体的动作贡献到底是多少时，可以把这个智能体的动作换成一个默认的动作，看看当前的动作跟默认的动作相比使得总体的得分增加了还是减少了，如果增加了，说明智能体的当前动作比默认动作好，如果减少了，则说明智能体当前动作比默认动作差。而这个默认的动作就称为基线。但这样做有个核心的问题，就是默认动作如何选择。常规的想法是选择默认动作需要依靠一套额外的网络进行评估，这无疑增加了整个训练网络难度。COMA算法中提出了利用当前的策略，以及当前的行为值函数对当前智能体的策略求解边缘分布来计算这个基线。通过这种方式，COMA可以避免设计额外的默认动作和额外的模拟计算，这里我么也引入COMA中的这个思想。
    这里我们通过把智能体i特定的动作值函数与所有智能体的平均动作价值做比较，进而可以得到单个智能体的特定行动是否会导致预期收益的增加或增加的奖励是否归因于其他智能体的行为，表达式如下：

利用Attention 机制我们可以计算得到一个形式更灵活的基线表达式，其不需要智能体具有相同的动作空间，也不需要一个共享的全局奖励，并且能够扩展到更多的智能体。这些优势都是通过对当前智能体进行编码得到$e_i$与其他智能体$x_i$的加权求和实现。
    求解这个优势函数的基线，从离散的角度考虑，需要在前项传播过程中传入当前智能体i所有可能的动作值来计算得到所有智能体的平均动作价值，计算期望的公式如下：

    为此我们需要从$Q_i$的输入中移除$a_i$并且输出所有动作值所对应的Q值。我们对每个智能体使用一个观测值的编码器$e_i=g_i^o(o_i)$来替换掉上文的$e_i=g_i(o_i,a_i)$，并且对$f_i$进行修改使之能够输出所有可能动作的Q值。从连续策略的角度，我们计算这个表达式有两种方法：⑴直接从智能体i的策略中抽样，近似得到平均值作为标准基线；⑵学习一个单独的值函数头，即这个值函数头把其他智能体的观测信息和动作信息当做输入。换句话说，就是把当没有智能体i参与时全局的值函数与有智能体i参数时对应的值函数做比较，两者的差值就是智能体i对应的优势函数。

iii.交叉熵

    交叉熵的强化学习思想由soft Actor-Critic算法中写到，这里我们将交叉熵引入到Actor网络和Critic网络的更新中。交叉熵的思想核心是不遗漏任何一个有用的信息，这与DDPG不同，DDPG算法如果找到一条最优路径，那么学习过程也就结束了。但是对于基于交叉熵的强化学习来说，神经网络要探索所有可能的最优路径用来学习。引入交叉熵有以下几个优势：⑴ 学到的策略可以作为更复杂具体任务的初始化。因为通过最大熵，策略不仅仅学到一种解决任务的方法，而是所有。因此这样的policy就更有利于去学习新的任务。⑵ 更强的探索能力能够更容易的在多模态下找到更好的模式。⑶具有更好的鲁棒性，因为要从不同的方式来探索各种最优的可能性，也因此面对干扰的时候能够更容易做出调整。
    下面是Critic网络的更新表达式：
$$L_Q(\psi )=\sum _{i=1}^N{E}_{(o,a,r,o^{\prime })-D}[(Q_i^{\psi }(o,a)-y_i{)}^2],where$$
$$y_i=r_i+\gamma E_{a^{\prime }-{\pi }_{{\theta }^{\prime }(o^{\prime })}}[Q_i^{{\psi }^{\prime }}(o^{\prime },a^{\prime })-\alpha \log ({\pi }_{{\theta }_i^{\prime }}(a_i^{\prime }|o_i^{\prime })]$$
其中，$\psi$'和θ’是目标Critic和目标Actor的参数。$Q_i^{\psi }$的输入是所有智能体的观测信息和动作信息。α是温度参数(与最大熵计算有关)平衡最大熵和回报。
    下面是Actor网络的更新表达式：

值得注意的是，我们采样的动作是从智能体当前的策略直接采样得到，而并不是像MADDPG那样通过经验回放采样，这样可以避免智能体的过渡泛华，以致于无法对当前策略调整。

二.实验部分

    作者通过实验研究验证两个主要的问题：⑴随着智能体数量的增加，不同算法的可扩展性；⑵评估关注与reward相关信息的能力，尤其是与reward相关的信息在动态变化时，每种算法是否还能有效地关注特定信息。
    对于⑴问题，实验的环境主要是Cooperate Treasure Collection(以下简称：CTC)环境，环境包含8个智能体，其中6个是“Treasure hunters”,2个是“treasure banks”。环境规则是每个“Treasure hunters”需要去收集对应颜色的treasure(treasure收集之后会随机再生)并把这些treasure放到正确颜色的“bank”中，而“bank”的任务就是尽可能多的从“hunters”那里收集treasure。所有的智能体都能知道其他智能体相对自己的位置，“hunters”会获得一个全局的reward对于其收集正确的treasure行为，而所有智能体都能获得一个全局reward对于正确放置treasure的行为。当然，如果“hunters”在收集过程中出现了碰撞现象会获得相应的惩罚。
    对于⑵问题，实验的主要环境是Rover-Tower Task(以下简称：RTT环境)，环境包含8个智能体，其中4个智能体是“rovers”,4个智能体是“towers”。环境规则是“rovers”不能看见周围的环境，只能依靠“towers”发来的信息，而“towers”不能移动，只能观测“rovers”的位置以及它们目标的位置，并把这些信息发给与其配对的“rovers”。
    实验中，为了便于验证统一使用了discrete polices,并且通信是集成到环境中的，并没有单独的使用一个模块进行通信，并且通信也被限制成了几个离散的信号。实验也对一些常规算法进行了改进，以满足检验“Attention”机制的效果，下图为实验比较的几种算法，其中“Uniform”是控制了所有智能体的权重是相同，之后是对应的实验结果：


    下面是对实验结果的分析：从回报和所需Attention的影响以及可扩展性两个方面分析。
    首先，分析的是回报和所需Attention对算法在环境中性能产生的影响。固定权重的Attention机制在CTC环境和Cooperative Navigation(以下简称CN)环境性能十分优秀，但在RTT环境中表现得却不是很好。相反，MADDPG以及其相应的改进算法MADDPG+SAC却在RTT环境中表现得很好，然而在CTC环境以及CN环境中十分的糟糕。
    对于CTC环境和CN环境而言，奖励是在智能体之间共享的，因此智能体的critic并不需要为了计算期望回报而关注特定的智能体的信息。此外，每个智能体的局部观测提供足够多的信息来进行合理的预测，这也就是MAAC算法（Uniform）性能超过预期的原因。对于RTT环境一个特定智能体的奖励值与一个观测智能体观测联系在了一起，在这种环境下，动态的Attention机制就起到了作用，智能体的子组交互并以单独的奖励执行协调的任务时，子组不会保持固定。这也就是为什么MAAC算法（Uniform）表现得不佳，本质在于关注特定智能体的信息对于预测期望回报是十分重要的。
    COMA算法使用单一的集中式网络通过前向传播来预测所有智能体的Q值。因此，这种方法可能在具有全局回报和动作空间相似的智能体（如合作导航CN环境）的环境中表现最佳，在这种环境中，我们看到COMA+SAC表现良好。另一方面，环境包含具有不同角色的智能体（RTT环境包含非全局奖励），则COMA与COMA+SAC算法表现都不太好。
     MADDPG（以及它改进算法MADDPG+SAC）在Rover-Tower环境中表现良好；但是，在CTC环境中的低性能是由于这个环境对于所有智能体而言，观察空间都比较大，因为MADDPG的Critic是将所有智能体的观察连接到每个智能体的Critic的单个输入向量中。
    接下来，分析的是扩展性对算法性能的影响。在CTC环境下，我们比较了MAAC算法和MADDPG+SAC算法的性能，MAAC算法随着智能体数量的增加，具有更好的可扩展性。MADDPG的Critic使用所有的信息都是非选择性的，而MAAC算法可以通过Attention机制了解哪些智能体需要在学习时更加注意，并将这些信息压缩成一个恒定大小的向量。因此，当智能体数量增加时，MAAC算法的扩展性更好。
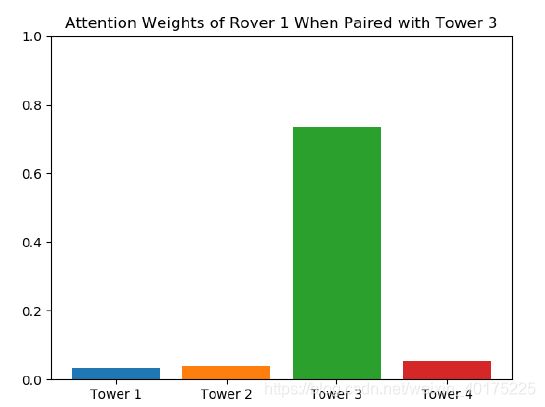
    最后，这篇论文还做了一个Attention可视化的工作，为了检查Attention机制是如何在更精细的层次上工作的。可视化了其中一个智能体的注意力权重，并通过分析数据，发现了与这个智能体配对的观测智能体。下图中，如果忽略其他智能体的权重（权重近似为0），可以发现，在没有任何明确的监督信息下，该智能体学会了关注与之配对的塔，即该模型隐式地学习哪个智能体与该智能体的预期未来收益最相关，并且该智能体可以动态地改变关注的对象而不影响算法的性能。

参考文献：
[1]Iqbal, Shariq, and Fei Sha. “Actor-Attention-Critic for Multi-Agent Reinforcement Learning” arXiv preprint arXiv:1810.02912 (2019).
[2] Foerster, Jakob N., et al. “Counterfactual multi-agent policy gradients” Thirty-Second AAAI Conference on Artificial Intelligence. 2018.
[3]T. Haarnoja, A. Zhou, P. Abbeel, and S. Levine. Soft actor-critic: Off-policy maximum entropy deepreinforcement learning with a stochastic actor. InInternational Conference on Machine Learning(ICML), volume 80, pages 1856–1865, 2018.10
[4]Tuomas Haarnoja, Aurick Zhou, Kristian Hartikainen,George Tucker, Sehoon Ha, Jie Tan, Vikash Kumar,Henry Zhu, Abhishek Gupta, Pieter Abbeel, et al. Softactor-critic algorithms and applications.arXiv preprintarXiv:1812.05905, 2018.