问题描述
小明需要在一篇文档中加入 N 张图片,其中第 i 张图片的宽度是 Wi,高度是 Hi。
假设纸张的宽度是 M,小明使用的文档编辑工具会用以下方式对图片进行自动排版:
1. 该工具会按照图片顺序,在宽度 M 以内,将尽可能多的图片排在一行。该行的高度是行内最高的图片的高度。例如在 M=10 的纸张上依次打印 3x4, 2x2, 3x3 三张图片,则效果如下图所示,这一行高度为4。(分割线以上为列标尺,分割线以下为排版区域;数字组成的矩形为第x张图片占用的版面)

2. 如果当前行剩余宽度大于0,并且小于下一张图片,则下一张图片会按比例缩放到宽度为当前行剩余宽度(高度向上取整),然后放入当前行。例如再放入一张4x9的图片,由于剩余宽度是2,这张图片会被压缩到2x5,再被放入第一行的末尾。此时该行高度为5:

3. 如果当前行剩余宽度为0,该工具会从下一行开始继续对剩余的图片进行排版,直到所有图片都处理完毕。此时所有行的总高度和就是这 N 张图片的排版高度。例如再放入11x1, 5x5, 3x4 的图片后,效果如下图所示,总高度为11:
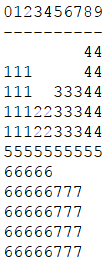
现在由于排版高度过高,图片的先后顺序也不能改变,小明只好从 N 张图片中选择一张删除掉以降低总高度。他希望剩余N-1张图片按原顺序的排版高度最低,你能求出最低高度是多少么?
假设纸张的宽度是 M,小明使用的文档编辑工具会用以下方式对图片进行自动排版:
1. 该工具会按照图片顺序,在宽度 M 以内,将尽可能多的图片排在一行。该行的高度是行内最高的图片的高度。例如在 M=10 的纸张上依次打印 3x4, 2x2, 3x3 三张图片,则效果如下图所示,这一行高度为4。(分割线以上为列标尺,分割线以下为排版区域;数字组成的矩形为第x张图片占用的版面)

2. 如果当前行剩余宽度大于0,并且小于下一张图片,则下一张图片会按比例缩放到宽度为当前行剩余宽度(高度向上取整),然后放入当前行。例如再放入一张4x9的图片,由于剩余宽度是2,这张图片会被压缩到2x5,再被放入第一行的末尾。此时该行高度为5:

3. 如果当前行剩余宽度为0,该工具会从下一行开始继续对剩余的图片进行排版,直到所有图片都处理完毕。此时所有行的总高度和就是这 N 张图片的排版高度。例如再放入11x1, 5x5, 3x4 的图片后,效果如下图所示,总高度为11:
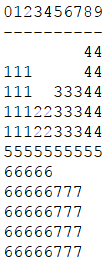
现在由于排版高度过高,图片的先后顺序也不能改变,小明只好从 N 张图片中选择一张删除掉以降低总高度。他希望剩余N-1张图片按原顺序的排版高度最低,你能求出最低高度是多少么?
输入格式
第一行包含两个整数 M 和 N,分别表示纸张宽度和图片的数量。
接下来 N 行,每行2个整数Wi, Hi,表示第 i 个图大小为 Wi*Hi。
对于30%的数据,满足1<=N<=1000
对于100%的数据,满足1<=N<=100000,1<=M, Wi, Hi<=100
接下来 N 行,每行2个整数Wi, Hi,表示第 i 个图大小为 Wi*Hi。
对于30%的数据,满足1<=N<=1000
对于100%的数据,满足1<=N<=100000,1<=M, Wi, Hi<=100
输出格式
一个整数,表示在删除掉某一张图片之后,排版高度最少能是多少。
样例输入
4 3
2 2
2 3
2 2
2 2
2 3
2 2
样例输出
2
样例输入
2 10
4 4
4 3
1 3
4 5
2 1
2 3
5 4
5 3
1 5
2 4
4 4
4 3
1 3
4 5
2 1
2 3
5 4
5 3
1 5
2 4
样例输出
17
解题思路:小明删除第 i 张图片时,第 1 到 i-1 张图片的排版不变,只有第 i+1 到 N 张图片的排版改变。并且如果用一个数组保存以第k张图片开始排版图片的高度,计算第 i+1 到 N 张图片
解题思路:小明删除第 i 张图片时,第 1 到 i-1 张图片的排版不变,只有第 i+1 到 N 张图片的排版改变。并且如果用一个数组保存以第k张图片开始排版图片的高度,计算第 i+1 到 N 张图片
改变后高度时就不需要全部计算,而只需要计算在换行之前受影响的高度+以之后图片开始排版的高度。
实现代码:
#include#include using namespace std; const int Max_N = 100000; const int INF = 1000000; struct paper//图片结构体 { int w; int h; paper(int w_,int h_){//构造函数 w = w_; h = h_; } paper(){} }; paper P[Max_N+1]; //输入 int N,M; int Rev[Max_N+2];//Rev[i]: 将 i-N 顺序加入最后的高度 void add(paper &p,int k)//在p的基础上加入第k个图片 p记录当前占用宽度和高度(这里p到代表某一行排列) { //加入时分两种情况考虑 if( p.w+P[k].w <= M )//加入图片宽度小于等于剩余宽度 (这时图片不需要收缩) { p.w += P[k].w; p.h = max( p.h, P[k].h ); } else {//加入图片宽度>剩余宽度 int w = M - p.w;//剩余宽度 p.h = max( p.h, ((w*P[k].h-1)/P[k].w)+1 );// wi/hi=w/h->h=w*hi/wi (-1,+1是处理向上取整) p.w = M; } } int getRev(paper p,int k)//在加入p的基础上加上k-N后排版的高度 { while( p.w N ) { add(p,k); k++; } return p.h + Rev[k]; } void solve() { for(int i=N; i>=1; i--)//初始化Rev[] { paper p(0,0); Rev[i] = getRev(p,i); } paper p(0,0); int res = INF, h = 0; for(int i=1; i<=N; i++) {//每次去掉第i个图片 res = min( res, h + getRev(p,i+1) );//h:1-i-1的高度, getRev(p,i+1):i+1-N高度 add(p,i); if( p.w==M ) { h += p.h;//更新当前排版高度 p.w = p.h = 0;//下一行 } } printf("%d\n",res); } int main() { scanf("%d%d",&M,&N); for(int i=1; i<=N; i++){ scanf("%d%d",&P[i].w,&P[i].h); } solve(); return 0; }
//参考链接https://blog.csdn.net/qq_20087731/article/details/106262655