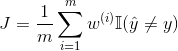花书+吴恩达深度学习(十九)构建模型策略(训练模型顺序、偏差方差、数据集划分、数据不匹配)
目录
0. 前言
1. 调试模型顺序
2. 偏差方差的解决方法
3. 数据集的选取划分
4. 数据不匹配问题
5. 评估指标的选取
6. 贝叶斯最佳误差
如果这篇文章对你有一点小小的帮助,请给个关注,点个赞喔~我会非常开心的~
花书+吴恩达深度学习(十八)迁移学习和多任务学习
花书+吴恩达深度学习(十九)构建模型策略(训练模型顺序、偏差方差、数据集划分、数据不匹配)
花书+吴恩达深度学习(二十)构建模型策略(超参数调试、监督预训练)
0. 前言
本篇文章主要记录,构建模型,调试模型中的一些技巧方法和注意事项。
- 训练集:用于训练模型参数的数据集
- 开发集:用于调试模型超参数的数据集(相当于平时所说的测试集)
- 测试集:只用于测试模型性能的数据集
1. 调试模型顺序
第一步,降低训练集上的代价函数。
如果不能有效的降低,可以尝试更大的神经网络,或更好的优化方法。
第二步,降低开发集上的代价函数。
如果不能有效的降低,考虑可能是过拟合,使用正则化,或使用更大的训练集。
第三步,降低测试集上的代价函数。
如果不能有效的降低,考虑可能是开发集太小和测试集不匹配,使用更大的开发集。
第四步,使其在真实世界中表现良好。
如果不能有效的表现,考虑可能是开发集或测试集设置选择的不正确,或者代价函数不能有效的评估误差。
附吴恩达深度学习这部分的课件:
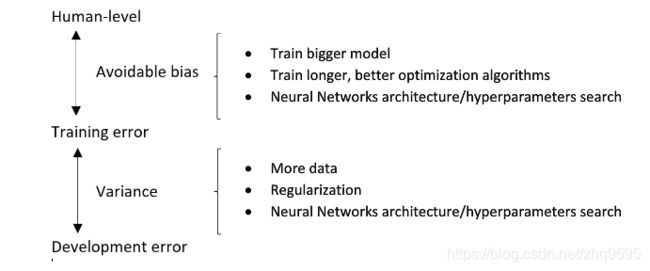
2. 偏差方差的解决方法
偏差,是指模型不能很好的学习到数据的普遍特性,所谓欠拟合。
- 训练更大的神经网络
- 使用更好的优化算法
- 搜索更好的超参数
- 使用不同的神经网络架构
方差,是指模型过于好的学习了数据,甚至学习了一些数据的个性,所谓过拟合。
- 更多的训练数据
- 使用正则化
- 搜索更好的超参数
- 使用不同的神经网络架构
贝叶斯最佳误差和训练集误差的差距,等效为偏差。
训练集误差和开发集误差的差距,等效为方差。
附吴恩达深度学习这部分的课件:
3. 数据集的选取划分
通常在选取数据集时,会随机选取。
因为为了使模型不失一般性,训练集开发集测试集应服从同一分布。
按照以前的数据量划分,可以划分为,![]() 或者
或者 ![]() ,诸如此类。
,诸如此类。
在大数据的情况下,例如有 ![]() 条数据,可能开发集和测试集仅各
条数据,可能开发集和测试集仅各 ![]() 数据就足够,
数据就足够,![]() ,诸如此类。
,诸如此类。
4. 数据不匹配问题
按照模型的一般性来说,训练集开发集和测试集的数据应属于同一分布。
但如果真实环境中,数据的分布与训练集不同,最好使得开发集和测试集的分布与真实环境相似。
例如,在图像识别中,训练集的数据是高清的,但是真实环境的图像是低像素的,最好使得开发集和测试集的数据也是低像素的。这样可以确保训练出来的模型可以在真实环境中识别图像。
当数据的分布不同时,方差的分析与之前不同。可能仅因为分布的不同,造成训练集误差和开发集误差的差距,称为数据不匹配,并不是过拟合的高方差。
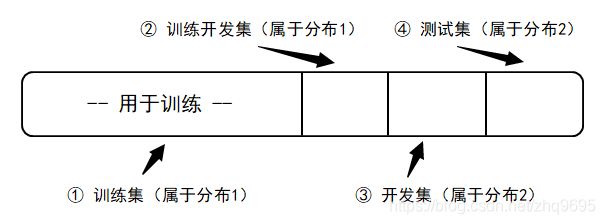
此时,可将数据如下划分:
从训练集中划分一部分作为训练开发集。
因训练集和训练开发集属于同一分布,当训练集误差和训练开发集误差有差距的时候,呈现的是高方差问题。
因训练开发集和开发集不属于同一分布,但都用于测试,当训练开发集误差和开发集误差有差距的时候,呈现的是数据不匹配问题。
解决数据不匹配的方法:使得训练集和开发集测试集的数据分布尽量相似,可将开发集和测试集部分数据分配至训练集,或者人工数据合成。
5. 评估指标的选取
对于 Precision 和 Recall ,不同的任务看重不同的指标。
例如,判断病人患病的情况,患病被判断为不患病代价更大(正类被判断成反类),更看重查全率 Recall 。给用户推荐商品的情况,推荐了很讨厌的商品比没有推荐到喜欢的商品代价更大(反类被判断成正类),更看重查准率 Precision 。
可以在代价函数上,对于判错的不同情况加上权重:
如果任务对不同的评估指标没有偏好。
那么尽量采用单一的评估指标,有利于比较不同模型。
例如,使用 F1-score 代替 Precision 和 Recall 。
6. 贝叶斯最佳误差
贝叶斯最佳误差是指,穷尽各种方法,可以达到的最低的误差。
在模型训练的时候,可以根据训练集误差和贝叶斯最佳误差的差距,来衡量偏差。
通常,以人类最好的误差,来近似贝叶斯最佳误差。
如果这篇文章对你有一点小小的帮助,请给个关注,点个赞喔~我会非常开心的~