Python之数据分析（间接联合排序、所有最值相关函数、有序插入、定积分、插值器对象）

一、间接联合排序

1、间接联合排序： 获取排序样本的下标后来排序0 1 2 3 4 5 6 7 8
原始序列：8 2 3 1 7 4 6 5 9
直接排序：1 2 3 4 5 6 7 8 9
间接排序：3 1 2 5 7 6 4 0 8

2、使用方法

• numpy.lexsort((参考序列, 待排序列))
  返回索引序列
• np.sort_complex(A)
  复数的排序，按照实部进行排，实部相同看虚部

3、练习代码

import numpy as np

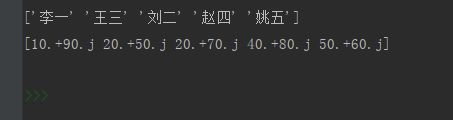
names = np.array(['李一', '刘二', '王三', '赵四', '姚五'])  # 存放姓名
scores = np.array([90, 70, 50, 80, 60])  # 存放分数
ages = np.array([10, 20, 20, 40, 50])  # 存放年龄

# 按照年龄升序排，年龄相同的参考分数排，最后输出他们的姓名
print(names[np.lexsort((scores, ages))])

# 对复数进行排序：复数是按照实部进行排序的
c = ages + scores * 1j  # 得到复数数组：用年龄当实部，分数乘单位向量当虚部
d = np.sort_complex(c)
print(d)

二、所有最值相关方法

1、成对最大值最小值

• max/min
• argmax/argmin
• nanmax/nanmin
• nanargmax/nanargmin

2、nan解释

• max：最大值
• min：最小值
• arg：间接，取下标
• nan：忽略无效值求最值

3、练习代码

import numpy as np

a = np.array([1, 2, np.nan, 4, 5])
print(np.max(a), np.min(a))  # nan既是最大值也是最小值
print(np.argmax(a), np.argmin(a))  # 取最值的下标（索引）
print(np.nanmax(a), np.nanmin(a))  # 忽略无效值的最值
print(np.nanargmax(a), np.nanargmin(a))  # 忽略无效值的最值下标

三、有序插入

1、引入
有序序列：[1, 2, 4, 5, 7, 8, 10]
被插序列：[6, 3]

2、调用方法

• numpy.searchsorted(有序序列, 被插序列)
  返回插入的位置
• numpy.insert(有序序列, 插入位置, 被插序列)
  直接插入，返回插入结果

3、练习代码

import numpy as np

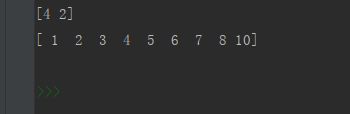
a = np.array([1, 2, 4, 5, 7, 8, 10])
b = np.array([6, 3])
c = np.searchsorted(a, b)  # 达到b有序插入在a后的位置下标
print(c)

# 直接插入
d = np.insert(a, c, b)  # 将b按照c的位置序列插入到a中
print(d)

四、定积分

1、导入库： import scipy.integrate as si

2、存原函数：
def f(x):
y = …x…
return y

3、上下限： a, b = __, __

4、求定积分： si.quad(f, a, b)[0]
返回的结果是定积分值

五、插值器对象

1、用处： 用于样本非常少，但又希望曲线足够平滑的时候。

2、使用步骤
1）import scipy.interpolate as si

2）si.interp1d(离散样本水平坐标, 离散样本垂直坐标, kind=‘插值器种类’)

返回一个一维插值器对象；
注意：p1d中间的是数字1，插值器种类默认的线性插值器
然后将该插值器对象当做函数去运行，传入参数：插值样本的水平坐标
最后会得到插值样本的垂直坐标

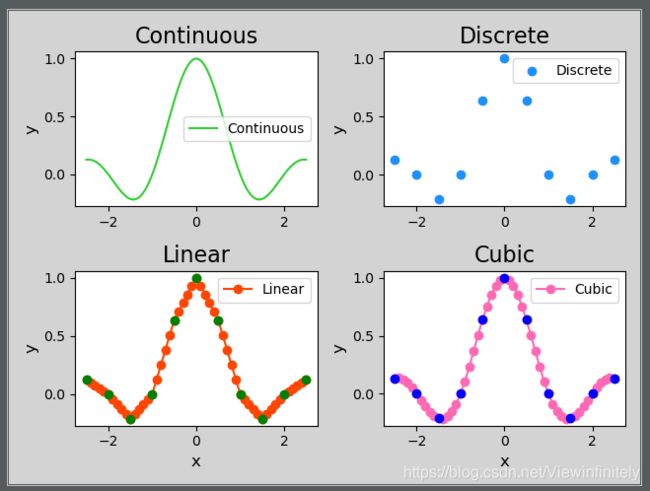
3、插值器案例（样本极少）

import numpy as np
import scipy.interpolate as si
import matplotlib.pylab as mp

min_x, max_x = -2.5, 2.5  # 标记水平坐标最值

# 连续曲线
con_x = np.linspace(min_x, max_x, 1001)  # 生成1000个原始信息
con_y = np.sinc(con_x)

# 离散曲线
dis_x = np.linspace(min_x, max_x, 11)
dis_y = np.sinc(dis_x)

# 线性插值器：将散点连接起来
linear = si.interp1d(dis_x, dis_y)  # 创建线性插值器
lin_x = np.linspace(min_x, max_x, 51)  # 插值横坐标
lin_y = linear(lin_x)

# 样条插值器
cubic = si.interp1d(dis_x, dis_y, kind='cubic')  # 需要加一个kind参数，因为默认是线性的
cub_x = np.linspace(min_x, max_x, 51)
cub_y = cubic(cub_x)

# 绘制连续曲线
mp.figure('Interpolation', facecolor='lightgray')
mp.subplot(2, 2, 1)
mp.title('Continuous', fontsize=16)
mp.ylabel('y', fontsize=12)
mp.tick_params(labelsize=10)
mp.plot(con_x, con_y, c='limegreen', label='Continuous')
mp.legend()

# 绘制离散样本曲线
mp.subplot(2, 2, 2)
mp.title('Discrete', fontsize=16)
mp.ylabel('y', fontsize=12)
mp.tick_params(labelsize=10)
# mp.plot(dis_x, dis_y, c='dodgerblue', label='Discrete')
mp.scatter(dis_x, dis_y, c='dodgerblue', label='Discrete')  # 散点图
mp.legend()

# 线性插值样本图（连接散点）
mp.subplot(2, 2, 3)
mp.title('Linear', fontsize=16)
mp.xlabel('x', fontsize=12)
mp.ylabel('y', fontsize=12)
mp.tick_params(labelsize=10)
mp.plot(lin_x, lin_y, 'o-', c='orangered', label='Linear')  # 散点图
mp.scatter(dis_x, dis_y, c='green', zorder=3)
mp.legend()

# 样条插值器图
mp.subplot(2, 2, 4)
mp.title('Cubic', fontsize=16)
mp.xlabel('x', fontsize=12)
mp.ylabel('y', fontsize=12)
mp.tick_params(labelsize=10)
mp.plot(cub_x, cub_y, 'o-', c='hotpink', label='Cubic')  # 散点图
mp.scatter(dis_x, dis_y, c='blue', zorder=3)
mp.legend()

mp.tight_layout()
mp.show()