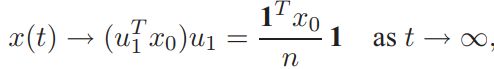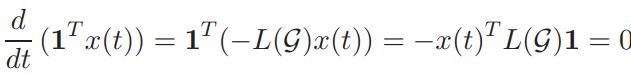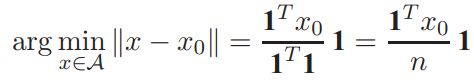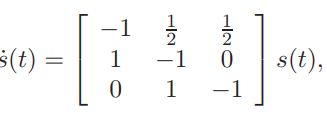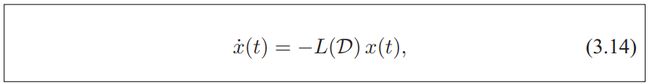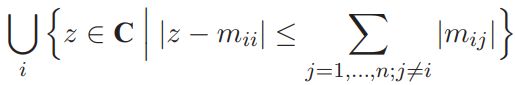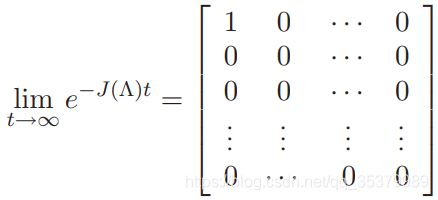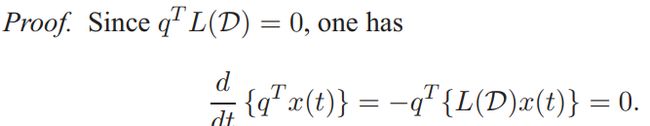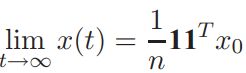多智能体中的图论——多智能体的一致性(二)
一致性(agreement)是多智能体协同(multiagent coordination)中的一个基础问题,即使智能体间达成一种共同状态。这一篇中我们考虑有向和无向静态网络中的一致性协议,首要目标是聚集在收敛(convergence)协议属性和潜在相互连接结构之间错综复杂的关系。
1、无向网络(邻接矩阵对称)
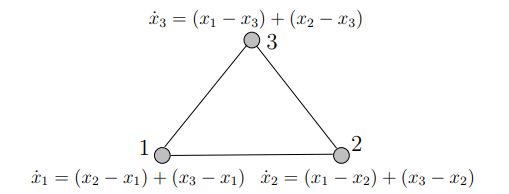
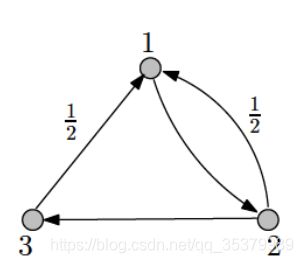
一致性协议涉及n个动态单元,将n个动态单元标记为1, 2,...,n,他们之间通过信息交换连接而相互连接。一个一致性协议的例子展示在下方
对于单元i,其一致性公式有:
其中N(i)为单元i所邻接单元的集合。但邻接矩阵为对称的(即为无向网络),整个一致性系统可表述为:
![]() (2.1)
(2.1)
即为多智能体的一阶一致性公式。
定义:一致点集![]() 是span{1}的子空间(span{1}表示已向量1为基的向量空间),则
是span{1}的子空间(span{1}表示已向量1为基的向量空间),则
对于一个连通无向图形的拉普拉斯谱,有
对应于零特征值![]() 的特征向量为1。需要注意的是L(G)是对称的,并且对于所有无向网络L(G)1=0.令
的特征向量为1。需要注意的是L(G)是对称的,并且对于所有无向网络L(G)1=0.令![]() 为L(G)中相互正交的特征向量(一个矩阵不同特征值对应的特征向量正交)。对应顺序的特征值对角阵为:
为L(G)中相互正交的特征向量(一个矩阵不同特征值对应的特征向量正交)。对应顺序的特征值对角阵为:
使用拉普拉斯因式分解有:
因此对于上边公式(2.1)有解(现代控制部分):初始![]()
定理:令G为一个连通图,一致协议(2.1)是以![]() 所控制的收敛速度收敛于一致点集。
所控制的收敛速度收敛于一致点集。
证明:对于一个连通图:![]()
因此有![]() ,
,![]() 作为最小拉普拉斯图形的正特征值,他控制着最慢的收敛速度。
作为最小拉普拉斯图形的正特征值,他控制着最慢的收敛速度。
需要注意的是随着各顶点达到一致点集,有:
因此。对于数![]() ,即在一致性协议中网络状态的质心,对于任何
,即在一致性协议中网络状态的质心,对于任何![]() 均为运动常量(constant of motion)。上述证明指出了一致收敛的协议到达预测初始状态轨道状态的产生,在欧几里得范数中达成一致子空间是由于:
均为运动常量(constant of motion)。上述证明指出了一致收敛的协议到达预测初始状态轨道状态的产生,在欧几里得范数中达成一致子空间是由于:
动态一致解的一般形式为2.3中,意指从任意状态的情况到达收敛至一致子空间,他是必要且充分的令![]() 因为正的
因为正的![]() 对应着G的连通性。对于一个渐进收敛到一致所需要的最小结构为相互联通的的网络中含有一棵生成树(spanning tree):
对应着G的连通性。对于一个渐进收敛到一致所需要的最小结构为相互联通的的网络中含有一棵生成树(spanning tree):
引理:对于收敛至一致子空间必要且充分的情况是潜在的图形含有一颗生成树
2、有向网络(非对称邻接矩阵)
将1中的双向信息交互转换为单向,如下图
可表述为:
上诉中可注意到,在网络中的每一个动态顶点对于其邻接的顶点有一个拉力,他将最后导致非对称网络中的顶点达到其初值所对应的权值平均位置。
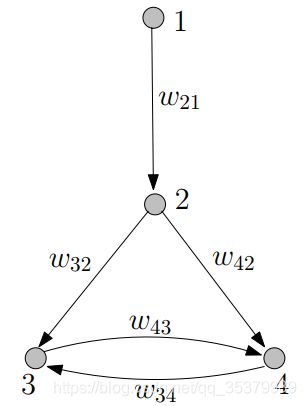
我们将概括收敛问题至有向赋权图(digraphs),思考在一阶动态下图3.8的收敛
系统的微分等式能够被表示为:
我们发现动态网络系统能够被表述为:
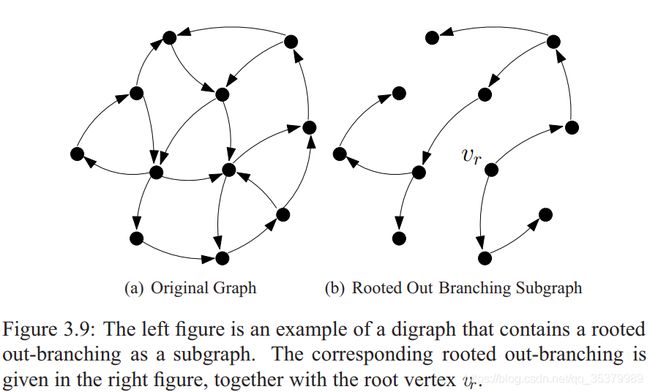
其中D为一个潜在顶点间互相连接的有向图
定义:一个有向图是根外分支(rooted out-branching)如果(1)不包含一个循环(2)具有一个根顶点vr(对于任何一个顶点都有一条通往顶点的通路)
命题: 一个具有n个顶点的有向图D包含一个根外分支作为子图有且仅有rank L(D)=n-1.在这种情况下,![]() 是以全部为1的向量为基的。(L(D)1=0).
是以全部为1的向量为基的。(L(D)1=0).
命题: 令D为一个n个顶点的赋权有向图,D的谱位于(即特征值)
其中![]() 为D中内度权值的最大值,也就是说对于任意一个有向图,L(D)的特征值具有非负实部。
为D中内度权值的最大值,也就是说对于任意一个有向图,L(D)的特征值具有非负实部。
命题: 令![]() 为有向图D拉普拉斯(内度)的约旦分解,当D包含一个根外分支,非奇异矩阵P可以被选为:(现代部分)
为有向图D拉普拉斯(内度)的约旦分解,当D包含一个根外分支,非奇异矩阵P可以被选为:(现代部分)
并且:![]()
证明:由现代控制知识
在这些结果的情况下,我们陈述有向赋权图主要的理论
定理:对于一个含有根外分支的有向图D,由3.14产生的状态轨道。初始化x0,满足:
其中p1和q1分别为L(D)中0特征值对应的左右特征向量,有![]() 。作为一个结果对于
。作为一个结果对于![]() 对于所有的初始状态有且只有D包含一个根外分支。
对于所有的初始状态有且只有D包含一个根外分支。
回想在无向图中一致协议运动常量为节点在任意时刻运动状态之和。类似地,我们能够发展在有向图中在3.14式的一个量。
命题: 令q为有向图内度拉普拉斯零特征值所对应的左特征向量,![]() 的值是保持不变的。
的值是保持不变的。
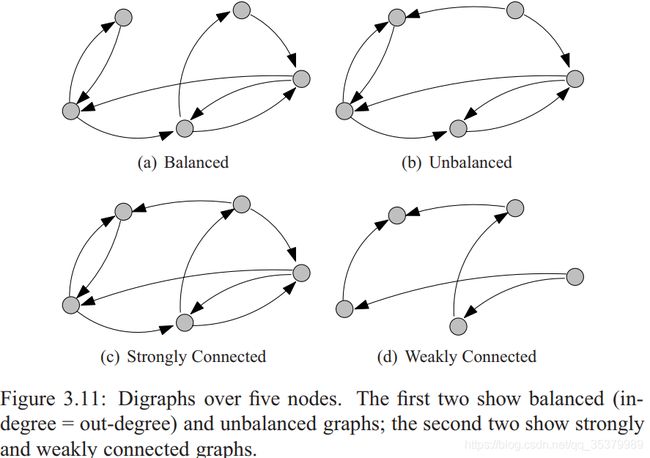
3、平衡图(balanced graph)
定义: 一个有向图如果被称为平衡图,则每个顶点的入度等于出度。
因此,如果有向图包含一个根外分支并且是平衡的,一致协议的公共值是各顶点初态的均值。
定义:一个有向图是强连接,如果在每对顶点之间有一条有向通路。
定义 :一个有向图是弱连接,如果他的迷失方向的感觉是连接的。
定理: 一个有向图的初始状态达成一致协议,有且只有他是弱连接并且是平衡的。