二维矩阵——从LeetCode题海中总结常见套路

二维矩阵的有套路吗？当然有，但是不如回溯、贪心这类题有模板，但是很多题的思路可以举一反三的

我大致分成四类：矩阵操作类，搜索矩阵类，动态规划类、回溯类

目录

矩阵操作类：

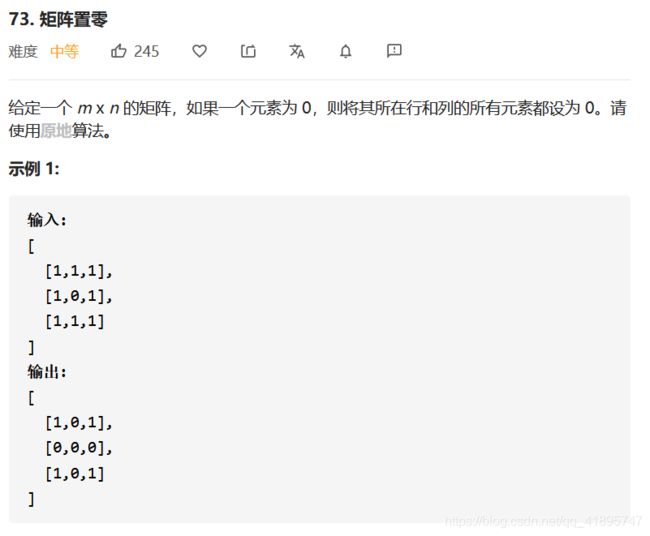
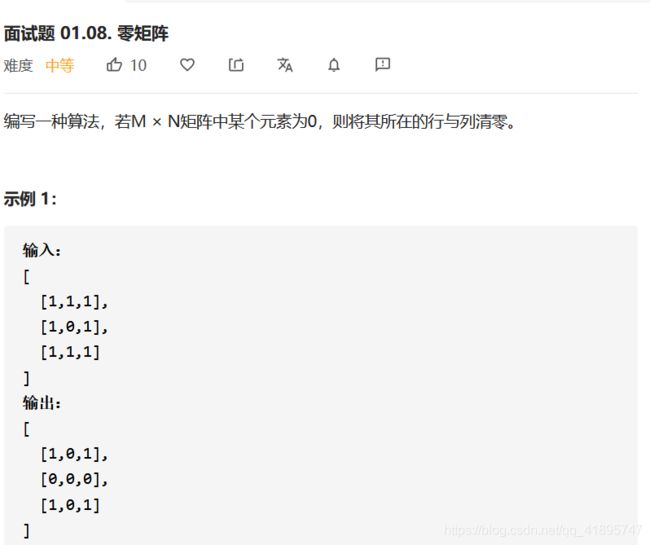
先遍历记录在清零的福利题：LeetCode.73矩阵置零&&面试题01.08.零矩阵

二维矩阵中的经典：LeetCode54.螺旋矩阵

搜索类：

剑指offer经典：LeetCode74.搜索二维矩阵

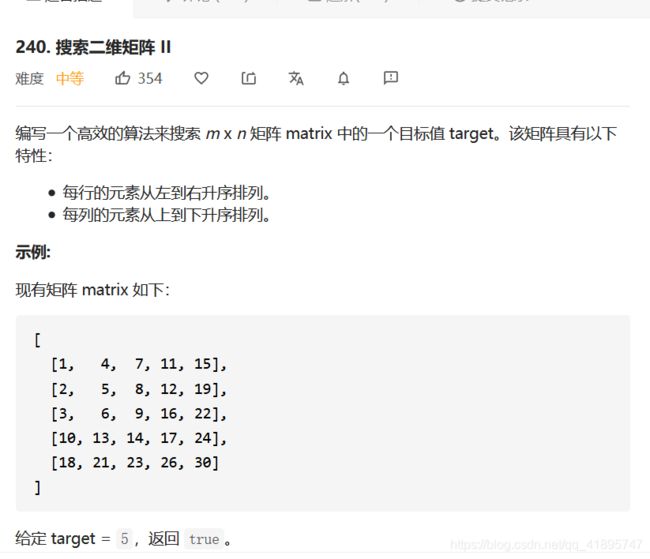
类似上一题的：LeetCode240.搜索二维矩阵II

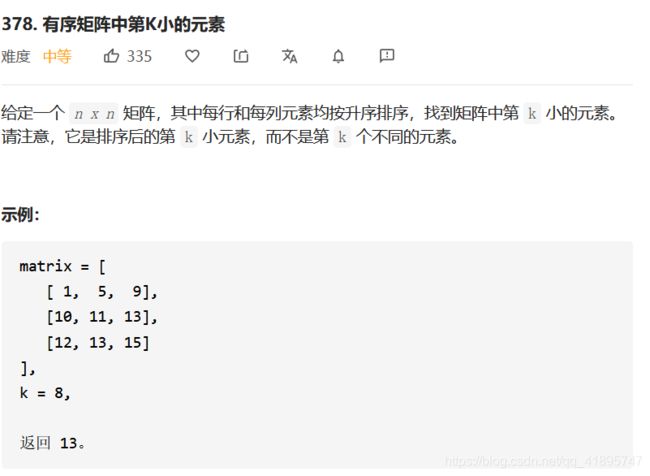
二维二分法：LeetCode378.有序矩阵中第K小的元素

动态规划类：

经典入门级DP：LeetCode62.不同路径

有障碍物的不同路径：LeetCode.63.不同路径II

DP记忆化搜索：LeetCode64.最小路径和

经典DP问题：LeetCode剑指offer47.礼物的最大价值

---

矩阵操作类：

先遍历记录在清零的福利题：LeetCode.73矩阵置零&&面试题01.08.零矩阵

思路有很多种，但是最后的复杂度都一样O(M+N)

这里使用的是先记录要清零的行数和列数，再遍历一遍进行清零

当然，拿到这题首先的思路是：呵呵，边遍历边清零不行么？当然不行，这样会影响下一个判断！

高赞的思路：

空间复杂度 O(2) ，用两个布尔变量就可以解决。方法就是利用数组的首行和首列来记录 0 值。从数组下标的 A[1][1] 开始遍历，两个布尔值记录首行首列是否需要置0。

这种思路和上面的大同小异，只是充分利用的矩阵的首行和首列，降低了空间复杂度

class Solution {
public:
    void setZeroes(vector>& matrix) {
        // 开辟两个一维数组存放要清零的行和列
        bool col[matrix.size()];
        bool row[matrix[0].size()];
        // 初始化
        for(int i = 0; i

class Solution {
public:
    void setZeroes(vector>& matrix) {
        // 开两个数组分别记录需要置零的行和列
        bool col[matrix.size()];
        bool row[matrix[0].size()];
        // 先初始化数组
        for(int i = 0; i

二维矩阵中的经典：LeetCode54.螺旋矩阵

这道题的思路很清晰，但是一次AC难度可不小，可以当做一个经典模板题来处理！

class Solution {
public:
    vector spiralOrder(vector>& matrix) {
        vector ans;
        if(matrix.empty()||matrix[0].empty())
            return ans;
        int up = 0, down = matrix.size()-1, left = 0, right = matrix[0].size()-1;
        while (true) {
            for(int i = left; i<=right; i++)
                ans.push_back(matrix[up][i]);
            if(++up>down)
                break;
            for(int i = up; i<=down; i++)
                ans.push_back(matrix[i][right]);
            if(--right=left; i--)
                ans.push_back(matrix[down][i]);
            if(--down=up; i--)
                ans.push_back(matrix[i][left]);
            if(++left>right)
                break;
        }
        return ans;
    }
};

搜索类：

剑指offer经典：LeetCode74.搜索二维矩阵

思路就是利用升序矩阵的性质，从右上角开始搜索，总的复杂度O(M+N)，还是比较理想的

这道题刷过剑指offer应该印象深刻吧！

class Solution {
public:
    bool searchMatrix(vector>& matrix, int target) {
        if(matrix.size()==0)
            return false;
        int i = 0; 
        int j = matrix[0].size()-1;
        while (i=0) {
            if ( matrix[i][j]>target ) {
                j--;
            }else if (matrix[i][j]

类似上一题的：LeetCode240.搜索二维矩阵II

class Solution {
public:
    bool searchMatrix(vector>& matrix, int target) {
        if(matrix.size()==0)
            return false;
        // 使用双指针从右上角进行查找
        int i = 0;
        int j = matrix[0].size()-1;
        while (i=0) {
            if(matrix[i][j]>target) {
                j--;
            }else if(matrix[i][j]

二维二分法：LeetCode378.有序矩阵中第K小的元素

这个二分比较难，思路上比较难

二分的基准是以整个矩阵中的mid，以这个mid统计矩阵有多少个数大于mid，多少个数小于mid

当然，在寻找mid的过程也要利用排序矩阵的性质

动态规划类：

经典入门级DP：LeetCode62.不同路径

超经典的一道DP入门题！

​

class Solution {
public:
    int uniquePaths(int m, int n) {
        // 代表当前节点所包含的路径总数
        int dp[m][n];   
        // 初始化首行和首列
        for (int i = 0; i

有障碍物的不同路径：LeetCode.63.不同路径II

完全可以从上面这题受到启发，就是多了进行障碍物处理的步骤

​

class Solution {
public:
    int uniquePathsWithObstacles(vector>& obstacleGrid) {
        int m = obstacleGrid.size();
        int n = obstacleGrid[0].size();
        // dp[i][j]表示通向坐标i,j的路径总数
        int dp[m][n];
        // 进行初始化
        int i;
        for(i = 0; i

DP记忆化搜索：LeetCode64.最小路径和

其实这道题和上面两题很相似，可以说是升级版本！

和下面这题找最大路径和可以说是套题哈哈

​

class Solution {
public:
    int minPathSum(vector>& grid) {
        int row = grid.size();
        int col = grid[0].size();
        int dp[row][col];   // dp[i][j]代表到达第i,j个空格所需要的最短路径
        dp[0][0] = grid[0][0];
        // 初始化
        for(int i = 1; i

经典DP问题：LeetCode剑指offer47.礼物的最大价值

这是一道超级经典的DP，建议先做62和63题，完全一个套路

​

class Solution {
public:
    int maxValue(vector>& grid) {
        // dp[i][j]表示(i,j)坐标下能拿到礼物的最大值
        int dp[grid.size()][grid[0].size()];
        dp[0][0] = grid[0][0];
        // 初始化
        for (int i = 1; i