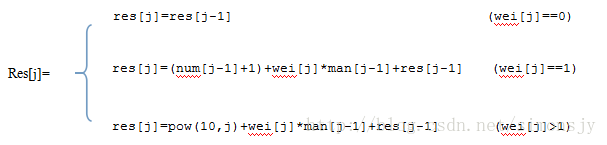google笔试题：写出这样一个函数 ,输入一个 n, 输出从1到这个数字之间的出现的1的个数

   这道题是传说中GOOGLE的笔试题目之一。

   题意比较明确，例如给出f(13)则输出6，f(100)输出21。

   理解题目之后，很容易判断出，这道题的基本思路。有些人利用暴力遍历的方法来求解，这种想法虽然很容易得到，但其效果很差。这个问题可以说是典型的递推求解问题，先不要着急写代码，先仔细想想能否得出一个递推的公式，然后利用for循环，每次求出一个递推解，最后得到答案。

我的思路如下：

从个位开始，将只有一位的数字视为一个部分解，

当出入数据为两位数是，会有一个公式，其中用到个位的部分解。

例如13 这个数字，1到23出现了6个1 ，  分别是 1 ，和10，11...19十位上的10个1，和11上各位上的一个1，还有21中的1。

将数字取得更大，比如213，便更可以找去其中的规律。

    最终解可以分为3个部分（在大多数情况下分为3个，递推题目的求解通常先考虑一般情况，然后再仔细斟酌边界情况和特殊情况，最终得到完整的递推方法）

1.部分解中1的个数*最高位数字。 例如213中 000~099和100~199中个位和十位上1的个数：20+20=40

2.如果最高位j上的数字大于1，则会有10的次方j个。例如213 中 100~199中百位上的1：100个（10的2次方）。

3.部分解中1的个数。例如213中 213中1的个数，即13中1的个数：6个。

仔细观察，可以看出这三种分类是以最高位来区分计算的。

wei[i]表示各位上的数字。

num[i]表示到第i位的数字。

man[i]表示0到i位最多有多少个1 例如00~99。

res[i]表示部分解。

则上面的分析表示为：

（1）res[j]=pow(10,j)+wei[j]*man[j-1]+res[j-1]

                        情况2           情况1                     情况3

（2）当然也有特殊情况，比如当最高为恰好为1，则最高位1的个数就不能使用上面的方法来计算了。

这种情况下的递推公式为：

res[j]=(num[j-1]+1)+wei[j]*man[j-1]+res[j-1]

                   情况2~                情况1                 情况3

（3）当递推时某一位是0时，计算到这一位的部分解就不需要那么复杂，直接就是：

res[j]=res[j-1]

综上所述：
可以得到通过第j位的数字的判断得出的递推公式

    最后需要求出在初始状态，也就是当j=0.即只有一位时的初始值。

1.if  wei[0]==0  res[0]=0

else res[0]=1

2.num[0]=wei[0]        num[j]=wei[j]*pow(10,j)+num[j-1]

3.man[0]=1    man[j]=pow(10,j)*man[j-1]+pow(10,j)

最后得到算法的主干部分如下：

for(j=0;j<=i;j++)
        {
                if(j==0){
                        num[j]=wei[j];
                        man[j]=1;
                        if(wei[j]==0) res[j]=0;
                        else res[j]=1;
                }
                else{
                        if(wei[j]==0) {res[j]=res[j-1];}
                        else if(wei[j]>1){res[j]=pow(10,j)+wei[j]*man[j-1]+res[j-1];}
                        else {res[j]=(num[j-1]+1)+wei[j]*man[j-1]+res[j-1];}
                        man[j]=pow(10,j)*man[j-1]+pow(10,j);
                        num[j]=wei[j]*pow(10,j)+num[j-1];

                }
         }

完整的程序如下：

#include
#include
#include
using namespace std;
int main()
{
        int n,i,j;
        int wei[100];
        int res[100];
        int man[100];
        int num[100];
        memset(wei,0,sizeof(int)*100);
        memset(res,0,sizeof(int)*100);
        memset(man,0,sizeof(int)*100);
        memset(num,0,sizeof(int)*100);
        cout<<"input the number!"<>n;
        i=0;
        while(n/10)
        {
                wei[i++]=n%10;
                n=n/10;
        }
        wei[i]=n;
        for(j=0;j<=i;j++)
        {
                if(j==0){
                        num[j]=wei[j];
                        man[j]=1;
                        if(wei[j]==0) res[j]=0;
                        else res[j]=1;
                }
                else{
                        if(wei[j]==0) {res[j]=res[j-1];}
                        else if(wei[j]>1){res[j]=pow(10,j)+wei[j]*man[j-1]+res[j-1];}
                        else {res[j]=(num[j-1]+1)+wei[j]*man[j-1]+res[j-1];}


                        man[j]=pow(10,j)*man[j-1]+pow(10,j);
                        num[j]=wei[j]*pow(10,j)+num[j-1];
                    }
        }
        cout<<"result is:"<

后记：

递推类型的问题需要注意的几点：

1.在编码之前一定要先求出完整正确的递推公式，切不可早求出一部分公式以后自认为剩余的部分比较简单，便直接开始编码，这样很容易产生错误，且这种错误不易检查出来。

2.推导递推公式时，正常的过程是先推导出一般情况下的递推公式，再仔细考虑边界和特殊情况下的递推公式，往往会有几种不同的情况。正如本体。这种做法很像在高等数学中求解分段函数的表达式时的场景，越是边界的地方，越容易出错，越是要仔细。

3.定义数组之后要，及时赋初值，如果数组要反复使用，那么在每次使用前都要重新赋初值。

这道题目也收录在编程之美这本书中，其中的解法我在这里就不过多陈述了。