并查集-代码实现
目录
一、并查集-数组模拟Quick Find-1
1、数组模拟Quick Find
二、改进:Quick Union-2
三、基于size的优化-Quick Union-3
四、基于Rank的优化-Quick Union-4
五、路径压缩-Quick Union-5
六、更理想的路径压缩-Quick Union-6
七、测试
一、并查集-数组模拟Quick Find-1
并查集解决的的问题——网络间节点的连接状态。
使用并查集可以快速的判断两个节点之间是否是相连接的。不同于求解两点之间的路径,并查集不关心两点之间是通过怎样的路径进行连接,正因为它没有求解其他不必要的结果,因此它的效率快。
首先我们定义一个并查集的接口:
public interface UF {
int getSize();
// 判断两个元素是否是相连的
boolean isConnected(int p, int q);
// 将两个元素合并在一起
void unionElements(int p, int q);
}1、数组模拟Quick Find
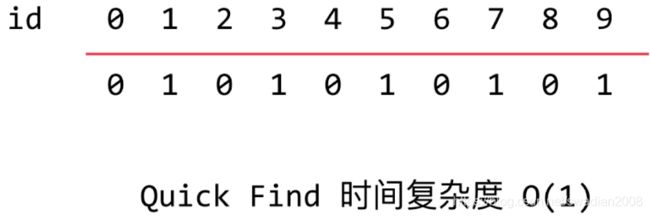
quick find 的实现逻辑,存储值为1-9的数据,对于数据1-9,他们所属的集合分成0和1;当需要判断两个数据是否是连接状态时,只需要判断这两个数据对应的集合是不是一样的。
比如0和2是相连接的,因为他们同属于0这个集合,而1和2是不相连接的,因为他们对应的集合分别是1和0;按照这种逻辑,当我们需要判断两个节点是否是相连接的时候,只需要比较他们所属的集合是否相同就可以了,这种操作的时间复杂度为O(1)。
但是,当isConnected操作为O(1)复杂度的时候,对应的unionElements操作就为O(n)的复杂度。因为,当执行unionElements(0,1)的时候,我们需要把所有对应的元素都遍历一遍,查找到属于0集合的元素,并全部改写成1集合,以实现合并操作。
简单的代码实现:
public class UnionFind1 implements UF{
private int[] id;
public UnionFind1(int size){
id = new int[size];
// 初始化的时候,每个元素都属于不同的集合
for (int i = 0; i < id.length; i++) {
id[i] = i;
}
}
@Override
public int getSize() {
return id.length;
}
@Override
public boolean isConnected(int p, int q) {
return find(p) == find(q);
}
// 合并元素p和元素q所属的集合
@Override
public void unionElements(int p, int q) {
int pID = find(p);
int qID = find(q);
// 两个元素如果本来就是属于相同的集合,就没有合并的并要
if (pID == qID) {
return;
}
for (int i = 0; i < id.length; i++) {
if (id[i] == pID) {
id[i] = qID;
}
}
}
// 查找元素p所对应的集合编号
private int find(int p){
if(p < 0 || p >= id.length){
throw new IllegalArgumentException("p is out of bound.");
}
return id[p];
}
}二、改进:Quick Union-2
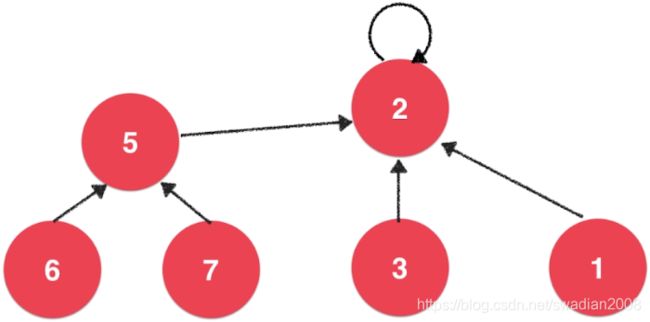
使用树的结构来实现并查集,此处并查集的树结构是倒过来的,由子节点指向父节点,它的是实现逻辑如下:
我们将每个元素都看成是一个节点,如图2是3的根节点(根节点2自己指向了自己),他们属于同一个集合;当节点1和节点3需要合并时,我们只要把节点的1的指针指向节点3的根节点2就可以了。同样的,节点7和3需要合并,此时把7所在树的根节点5的指针指向节点3的根节点2就可以了,此时,完成了7所在树的所有节点的合并操作。
对于数据的初始化操作,一开始,所有元素都是一颗独立的树
此处,我们仍然使用数组的形式来进行索引存储
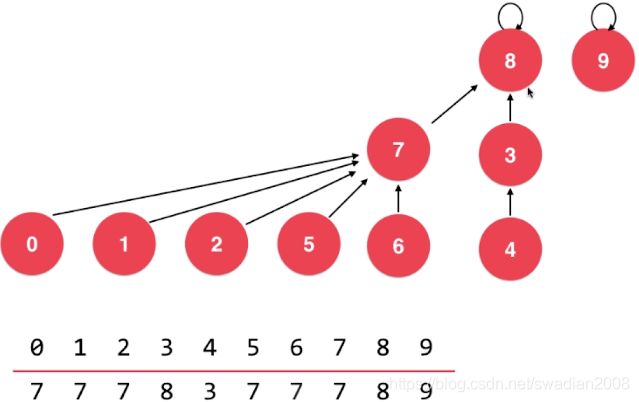
实现相关并操作后的结构图示示例:
根据树结构实现的并查集:
public class UnionFind2 implements UF {
private int[] parent;
public UnionFind2(int size){
parent = new int[size];
// 初始化的时候,所有的元素都是一个独立的树
for (int i = 0; i < parent.length; i++) {
parent[i] = i;
}
}
@Override
public int getSize() {
return parent.length;
}
@Override
public boolean isConnected(int p, int q) {
return find(p) == find(q);
}
@Override
public void unionElements(int p, int q) {
// 查找根节点所属集合
int pRoot = find(p);
int qRoot = find(q);
if(pRoot == qRoot){
return;
}
// 把根节点的指针指向q进行合并
parent[pRoot] = qRoot;
}
// 查找元素p所对应的集合编号,时间复杂度为O(h)
private int find(int p){
if (p < 0 || p >= parent.length) {
throw new IllegalArgumentException("p is out of bound.");
}
// 判断是不是根节点(根节点自己等于自己)
while(p != parent[p]){
p = parent[p];
}
return p;
}
}使用树状结构的好处是缩短了查询的时间复杂度,相比使用数组进行实现的时间复杂度O(n),明显O(log(n))的效率要高很多。对于使用树来说,算法的遍历深度只跟树的层级有关。
三、基于size的优化-Quick Union-3
在我们使用特殊的树状结构来实现并查集的时候,我们只是把树进行了简单的合并,并没有考虑到树的形状。
// 把根节点的指针指向q进行合并
parent[pRoot] = qRoot;那么,当有如下并查集数据,要实现Union(4,9),按照我们之前的逻辑是把8指向9(8—>9)这样来实现,此时8为根节点的树的层级为3,执向9以后,9为根节点的树的层级结构为4,我们发现并查集的层级增加了(意味着遍历深度又增加了)。更有极端的情况是整棵树退化成一个链表的结构,使得树的层级就等于节点的个数,算法的复杂度退化成了O(n)级别。
那么,有没有办法减少树的层级呢?
我们可以尝试使用size,对比两个将要合并的节点,比较他们的所在树的节点个数,我们让节点个数少的节点合并到节点个数多的那个节点上,如图,我们不让8—>9,而是让9—>8;这样操作的结果,就是树的层级没有改变,仍然是3层。
接下来,我们修改一下代码,只要在Quick Union-2的基础上,新增一个维护变量sz,sz[i]表示以i为根的集合元素个数。
private int[] sz; // sz[i]表示以i为根的集合元素个数
public UnionFind3(int size){
parent = new int[size];
sz = new int[size];
// 初始化的时候,所有的元素都是一个独立的树
for (int i = 0; i < size; i++) {
parent[i] = i;
// 每一集合一开始都只有一个元素
sz[i] = 1;
}
}然后更改索引的指向逻辑,把要实现合并的节点少的树的根节点指向节点多的树的根节点,其他逻辑不变
// 如果pRoot节点的数量小于qRoot节点的数量,pRoot->qRoot
if(sz[pRoot] < sz[qRoot]){
parent[pRoot] = qRoot;
// 树的节点数量维护
sz[qRoot] += sz[pRoot];
}else{// qRoot->pRoot
parent[qRoot] = pRoot;
// 树的节点数量维护
sz[pRoot] += sz[qRoot];
}整体代码如下:
public class UnionFind3 implements UF {
private int[] parent;
private int[] sz; // sz[i]表示以i为根的集合元素个数
public UnionFind3(int size){
parent = new int[size];
sz = new int[size];
// 初始化的时候,所有的元素都是一个独立的树
for (int i = 0; i < size; i++) {
parent[i] = i;
// 每一集合一开始都只有一个元素
sz[i] = 1;
}
}
@Override
public int getSize() {
return parent.length;
}
@Override
public boolean isConnected(int p, int q) {
return find(p) == find(q);
}
@Override
public void unionElements(int p, int q) {
// 查找根节点所属集合
int pRoot = find(p);
int qRoot = find(q);
if(pRoot == qRoot){
return;
}
// 如果pRoot节点的数量小于qRoot节点的数量,pRoot->qRoot
if(sz[pRoot] < sz[qRoot]){
parent[pRoot] = qRoot;
// 树的节点数量维护
sz[qRoot] += sz[pRoot];
}else{// qRoot->pRoot
parent[qRoot] = pRoot;
// 树的节点数量维护
sz[pRoot] += sz[qRoot];
}
}
// 查找元素p所对应的集合编号,时间复杂度为O(h)
private int find(int p){
if (p < 0 || p >= parent.length) {
throw new IllegalArgumentException("p is out of bound.");
}
// 判断是不是根节点(根节点自己等于自己)
while(p != parent[p]){
p = parent[p];
}
return p;
}
}四、基于Rank的优化-Quick Union-4
基于size的维护其实还存在一个问题,那就是当合并节点“7”所在树的size > 另一个合并节点“8”所在树的size;但是节点“8”所在树的深度却要比节点“7”所在树的深度要高,如图。
按照我们原有的逻辑,实现的结果是这样的,树的层级由最高为3,变成了最高为4,结合的深度又增加了。
按照之前我们对算法的分析,应该把深度低的树指向深度高的树,这样的操作结果才是最合理的,因为不会增加树的层级,如下效果:
接下来,我们在之前的代码上继续进行优化,在Quick Union-3的基础上我们不再维护size了,转而维护树的深度rank;
private int[] parent;
private int[] rank; // rank[i]表示以i为根的集合所表示的树的层数
public UnionFind4(int size){
parent = new int[size];
rank = new int[size];
// 初始化的时候,所有的元素都是一个独立的树
for (int i = 0; i < size; i++) {
parent[i] = i;
// 每个集合一开始的层级都是1
rank[i] = 1;
}
}我们根据深度来实现合并的逻辑
// 将rank低的集合合并到rank高的集合上
if(rank[pRoot] < rank[qRoot]){
parent[pRoot] = qRoot;
}else if(rank[pRoot] > rank[qRoot]){// qRoot->pRoot
parent[qRoot] = pRoot;
}else{// parent[pRoot] == parent[qRoot]
parent[qRoot] = pRoot;
rank[pRoot] += 1;
}整体的代码实现如下:
public class UnionFind4 implements UF {
private int[] parent;
private int[] rank; // rank[i]表示以i为根的集合所表示的树的层数
public UnionFind4(int size){
parent = new int[size];
rank = new int[size];
// 初始化的时候,所有的元素都是一个独立的树
for (int i = 0; i < size; i++) {
parent[i] = i;
// 每个集合一开始的层级都是1
rank[i] = 1;
}
}
@Override
public int getSize() {
return parent.length;
}
@Override
public boolean isConnected(int p, int q) {
return find(p) == find(q);
}
@Override
public void unionElements(int p, int q) {
// 查找根节点所属集合
int pRoot = find(p);
int qRoot = find(q);
if(pRoot == qRoot){
return;
}
// 将rank低的集合合并到rank高的集合上
if(rank[pRoot] < rank[qRoot]){
parent[pRoot] = qRoot;
}else if(rank[pRoot] > rank[qRoot]){// qRoot->pRoot
parent[qRoot] = pRoot;
}else{// parent[pRoot] == parent[qRoot]
parent[qRoot] = pRoot;
rank[pRoot] += 1;
}
}
// 查找元素p所对应的集合编号,时间复杂度为O(h)
private int find(int p){
if (p < 0 || p >= parent.length) {
throw new IllegalArgumentException("p is out of bound.");
}
// 判断是不是根节点(根节点自己等于自己)
while(p != parent[p]){
p = parent[p];
}
return p;
}
}五、路径压缩-Quick Union-5
所谓的路径压缩,是针对树的深度来说的,一般情况下,一棵树它的层级越低,它的查询效率越快;如果是退化成链表的情况,查询元素,需要从头到尾遍历整个集合,所以它的效率是最差的。因此,我们需要想办法压缩整棵树的高度,来提高数据结构的运算效率。
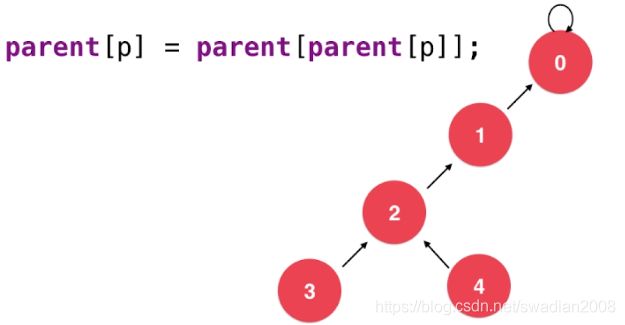
如果,我们在每一次查询的时候,发现节点的父亲节点还有一个有父亲节点,那么就让这个节点指向父亲节点的父亲节点,即执行一次 parent[p] = parent[parent[p]];便可以对树结构进行有效的路劲压缩。
在代码中的实现也比较简单,我们只要在Quick Union-4的基础上,改变一下查询的方法就可以了,如下,在查询方法中添加一行代码: parent[p] = parent[parent[p]];
// 查找元素p所对应的集合编号,时间复杂度为O(h)
private int find(int p){
if (p < 0 || p >= parent.length) {
throw new IllegalArgumentException("p is out of bound.");
}
// 判断是不是根节点(根节点自己等于自己)
while(p != parent[p]){
parent[p] = parent[parent[p]];
p = parent[p];
}
return p;
}整体的实现代码如下:
public class UnionFind5 implements UF {
private int[] parent;
private int[] rank; // rank[i]表示以i为根的集合所表示的树的层数
public UnionFind5(int size){
parent = new int[size];
rank = new int[size];
// 初始化的时候,所有的元素都是一个独立的树
for (int i = 0; i < size; i++) {
parent[i] = i;
// 每个集合一开始的层级都是1
rank[i] = 1;
}
}
@Override
public int getSize() {
return parent.length;
}
@Override
public boolean isConnected(int p, int q) {
return find(p) == find(q);
}
@Override
public void unionElements(int p, int q) {
// 查找根节点所属集合
int pRoot = find(p);
int qRoot = find(q);
if(pRoot == qRoot){
return;
}
// 将rank低的集合合并到rank高的集合上
if(rank[pRoot] < rank[qRoot]){
parent[pRoot] = qRoot;
}else if(rank[pRoot] > rank[qRoot]){// qRoot->pRoot
parent[qRoot] = pRoot;
}else{// parent[pRoot] == parent[qRoot]
parent[qRoot] = pRoot;
rank[pRoot] += 1;
}
}
// 查找元素p所对应的集合编号,时间复杂度为O(h)
private int find(int p){
if (p < 0 || p >= parent.length) {
throw new IllegalArgumentException("p is out of bound.");
}
// 判断是不是根节点(根节点自己等于自己)
while(p != parent[p]){
parent[p] = parent[parent[p]];
p = parent[p];
}
return p;
}
}注意:rank在进行路径压缩后并不是真正代表的树的深度,有时候,一个层级的节点,它们的rank值并不相同,所以路径压缩后的rank更相当于表示一个排序。同时,我们也不一定要刻意去维护一棵树的精确深度,在并查集中,这样是没有意义的,反而会增加数据结构的性能消耗。
六、更理想的路径压缩-Quick Union-6
前边我们也提到了,并查集树的深度越低,它的效率越快,那么我们可不可以查找一个节点时,直接把它的索引指向根节点,进行如下图这种扁平式的优化呢?
答案是可以的,我们需要借助递归的实现,在查询的逻辑中,使用递归实现的代码如下
// 查找元素p所对应的集合编号,时间复杂度为O(h)
private int find(int p){
if (p < 0 || p >= parent.length) {
throw new IllegalArgumentException("p is out of bound.");
}
// 判断是不是根节点
if(p != parent[p]){
parent[p] = find(parent[p]);
}// 返回根节点
return parent[p];
}这段代码的逻辑是,我们不停的去查找根节点的索引,直到查找到为止。通过这段代码逻辑,我们可以直接把当前查找节点的索引指向到树的根节点上。
注:因为递归是需要消耗性能的,Quick Union-6 的效率要比Quick Union-5(非递归实现)要差一点,在此这种实现仅作参考。
七、测试
对于上述实现的并查集,可以通过以下简单的测试程序进行测试
public class Main {
private static double testUF(UF uf, int m) {
// 一共维护了多少数据
int size = uf.getSize();
Random random = new Random();
long startTime = System.nanoTime();
// 首先进行m次的合并操作
for (int i = 0; i < m; i++) {
int a = random.nextInt(size);
int b = random.nextInt(size);
uf.unionElements(a, b);
}
// 然后再进行m次的查询操作
for (int i = 0; i < m; i++) {
int a = random.nextInt(size);
int b = random.nextInt(size);
uf.isConnected(a, b);
}
long endTime = System.nanoTime();
return (endTime - startTime) / 1000000000.0;
}
public static void main(String[] args) {
int size = 10000000;
int m = 10000000;
// UnionFind1 uf1 = new UnionFind1(size);
// System.out.println("UnionFind1:" + testUF(uf1, m) + "s");
//
// UnionFind2 uf2 = new UnionFind2(size);
// System.out.println("UnionFind2:" + testUF(uf2, m) + "s");
UnionFind3 uf3 = new UnionFind3(size);
System.out.println("UnionFind3:" + testUF(uf3, m) + "s");
UnionFind4 uf4 = new UnionFind4(size);
System.out.println("UnionFind4:" + testUF(uf4, m) + "s");
UnionFind5 uf5 = new UnionFind5(size);
System.out.println("UnionFind5:" + testUF(uf5, m) + "s");
UnionFind6 uf6 = new UnionFind6(size);
System.out.println("UnionFind6:" + testUF(uf6, m) + "s");
}
}