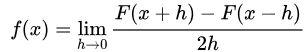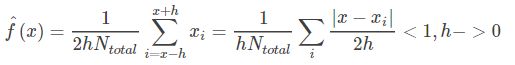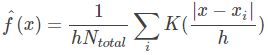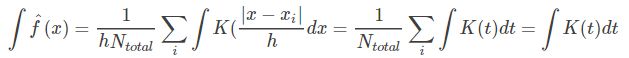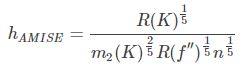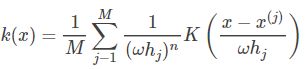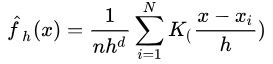核密度估计 Kernel Density Estimation(KDE)
目录
1 分布密度函数
1.1 参数估计方法
1.2 非参数估计
2 直方图到核密度估计
2.1 核函数
2.2 带宽的选择
2.2.1 自适应或可变带宽的核密度估计
2.3 多维
1 分布密度函数
给定一个样本集,怎么得到该样本集的分布密度函数,解决这一问题有两个方法:
1.1 参数估计方法
简单来讲,即假定样本集符合某一概率分布,然后根据样本集拟合该分布中的参数,例如:似然估计,混合高斯等,由于参数估计方法中需要加入主观的先验知识,往往很难拟合出与真实分布的模型;
1.2 非参数估计
和参数估计不同,非参数估计并不加入任何先验知识,而是根据数据本身的特点、性质来拟合分布,这样能比参数估计方法得出更好的模型。核密度估计就是非参数估计中的一种,由Rosenblatt (1955)和Emanuel Parzen(1962)提出,又名Parzen窗(Parzen window)。Ruppert和Cline基于数据集密度函数聚类算法提出修订的核密度估计方法。
2 直方图到核密度估计
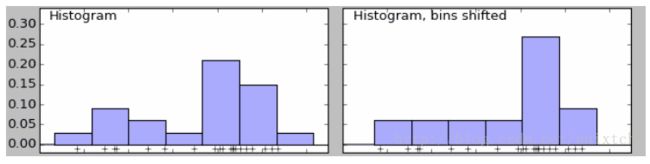
给定一个数据集,需要观察这些样本的分布情况,往往我们会采用直方图的方法来进行直观的展现。该直方图的特点是简单易懂,但缺点在于以下三个方面:(1)密度函数是不平滑的;(2)密度函数受子区间(即每个直方体)宽度影响很大,同样的原始数据如果取不同的子区间范围,那么展示的结果可能是完全不同的。如下图中的前两个图,第二个图只是在第一个图的基础上,划分区间增加了0.75,但展现出的密度函数却看起来差异很大;(3)直方图最多只能展示2维数据,如果维度更多则无法有效展示。
除此之外,直方图还存在一个问题,那就是直方图展示的分布曲线并不平滑,即在一个bin中的样本具有相等的概率密度,显然,这一点往往并不适合。解决这一问题的办法时增加bins的数量,当bins增到到样本的最大值时,就能对样本的每一点都会有一个属于自己的概率,但同时会带来其他问题,样本中没出现的值的概率为0,概率密度函数不连续,这同样存在很大的问题。如果我们将这些不连续的区间连续起来,那么这很大程度上便能符合我们的要求,其中一个思想就是对于样本中的某一点的概率密度,如果能把邻域的信息利用起来,那么最后的概率密度就会很大程度上改善不连续的问题,为了方便观察,我们看另外一副图。
一个很自然的想法是,如果我们想知道X=x处的密度函数值,可以像直方图一样,选一个x附近的小区间,数一下在这个区间里面的点的个数,除以总个数,应该是一个比较好的估计。用数学语言来描述,如果你还记得导数的定义,密度函数可以写为:
现在我们假设要求x处的密度函数值,根据上面的思想,如果取 x 的邻域[x-h,x+h],当h->0的时候,我们便能把该邻域的密度函数值当作x点的密度函数值。用数学语言写就是:
![]() 是该邻域中的样本点数量,
是该邻域中的样本点数量,![]() 样本集的总数量,最后对该邻域内的密度值取平均便得到 x 点的密度函数值f(x)。把上面的式子进行改写,即:核密度估计(Kernel density estimation),是一种用于估计概率密度函数的非参数方法,
样本集的总数量,最后对该邻域内的密度值取平均便得到 x 点的密度函数值f(x)。把上面的式子进行改写,即:核密度估计(Kernel density estimation),是一种用于估计概率密度函数的非参数方法,![]() 为独立同分布 F 的n 个样本点,设其概率密度函数为 f:
为独立同分布 F 的n 个样本点,设其概率密度函数为 f:
这里 h 如果选的太大,肯定不符合 h 趋向于 0 的要求。h 选的太小,那么用于估计 f(x) 的点实际上非常少。这也就是非参数估计里面的 bias-variance tradeoff,也就是偏差和方差的平衡。这样后还是存在一个问题,那就是概率密度函数依然不够平滑(因为两个数之间的存在无数个数)。
记 ![]() ,那么:
,那么:
由于需要满足概率密度的积分为1,所以:
也就是要满足 K(t) 的积分等于1也就满足了![]() 的积分为1。如果把 K(t) 当作其他已知的概率密度函数,那么问题就解决了,最后的密度函数也就连续了。
的积分为1。如果把 K(t) 当作其他已知的概率密度函数,那么问题就解决了,最后的密度函数也就连续了。
2.1 核函数
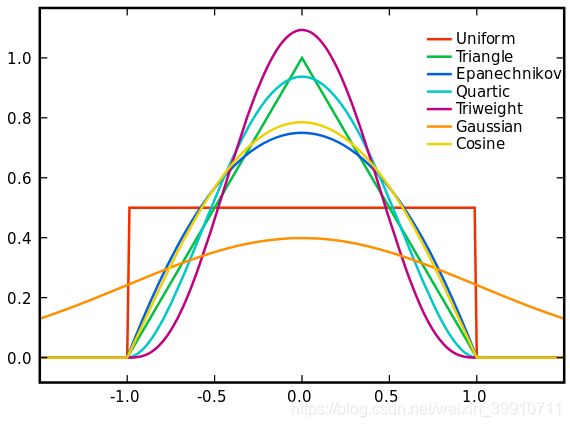
从支持向量机、meansift都接触过核函数,应该说核函数是一种理论概念,但每种核函数的功能都是不一样的,这里的核函数有uniform,triangular, biweight, triweight, Epanechnikov,normal等。这些核函数的图像大致如下图:
有言论称Epanechnikov 内核在均方误差意义下是最优的,效率损失也很小。由于高斯内核方便的数学性质,也经常使用 K(x)= ϕ(x),ϕ(x)为标准正态概率密度函数。
从上面讲述的得到的是样本中某一点的概率密度函数,那么整个样本集应该是怎么拟合的呢?将设有N个样本点,对这N个点进行上面的拟合过后,将这N个概率密度函数进行叠加便得到了整个样本集的概率密度函数。例如利用高斯核对X={x1=−2.1,x2=−1.3,x3=−0.4,x4=1.9,x5=5.1,x6=6.2} 六个点的“拟合”结果如下:
- 在直方图中,横轴间隔为2,数据落到某个区间,此区间y轴增加1/12。
- 在核密度估计中,另正态分布方差为2.25,红色的虚线表示由每一个数据得到的正态分布,叠加一起得到核密度估计的结果,蓝色表示。
那么问题就来了,如何选定核函数的“方差”呢?这其实是由h来决定,不同的带宽下的核函数估计结果差异很大,如下图:
(Kernel density estimate (KDE) with different bandwidths of a random sample of 100 points from a standard normal distribution. Grey: true density (standard normal). Red: KDE with h=0.05. Black: KDE with h=0.337. Green: KDE with h=2.)
2.2 带宽的选择
在核函数确定之后,比如上面选择的高斯核,那么高斯核的方差,也就是h(也叫带宽,也叫窗口,我们这里说的邻域)应该选择多大呢?不同的带宽会导致最后的拟合结果差别很大。同时上面也提到过,理论上h->0的,但h太小,邻域中参与拟合的点就会过少。那么借助机器学习的理论,我们当然可以使用交叉验证选择最好的h。另外,也有一个理论的推导给你选择h提供一些信息。
在样本集给定的情况下,我们只能对样本点的概率密度进行计算,那拟合过后的概率密度应该和计算的值更加接近才好,基于这一点,我们定义一个误差函数,然后最小化该误差函数便能为h的选择提供一个大致的方向。选择最小化L2风险函数,即均平方积分误差函数(mean intergrated squared error),该函数的定义是:
在weak assumptions下,![]() ,其中AMISE为渐进的MISE。而AMISE有:
,其中AMISE为渐进的MISE。而AMISE有:
其中:
最小化MISE(h)等价于最小化AMISE(h),求导,令导数为0有:
得:
当核函数确定之后,h公式里的R、m、f”都可以确定下来,h便存在解析解。
有:![]()
如果带宽不是固定的,其变化取决于估计的位置(balloon estimator)或样本点(逐点估计pointwise estimator),由此可以产生一个非常强大的方法称为自适应或可变带宽核密度估计。
如果使用高斯核函数进行核密度估计,则 h 的最优选择(即使平均积分平方误差最小化的带宽)为
这里 ![]() 是样品的标准差。这种近似称为正态分布近似,高斯近似,或Silverman(1986)经验法则。虽然这个经验法则很容易计算,但应谨慎使用,因为当密度不接近正态时,可能会产生泛化极差的估计。
是样品的标准差。这种近似称为正态分布近似,高斯近似,或Silverman(1986)经验法则。虽然这个经验法则很容易计算,但应谨慎使用,因为当密度不接近正态时,可能会产生泛化极差的估计。
这里带宽的作用简述:
- 在数据可视化的相关领域中,带宽的大小决定了核密度估计函数(KDE)的平滑(smooth)程度,带宽越小越undersmooth,带宽越大越oversmooth。
- 在POI兴趣点推荐领域,或位置服务领域,带宽h的设置主要与分析尺度以及地理现象特点有关。较小的带宽可以使密度分布结果中出现较多的高值或低值区域,适合于揭示密度分布的局部特征,而较大的带宽可以在全局尺度下使热点区域体现得更加明显。另外,带宽应与兴趣点的离散程度呈正相关,对于稀疏型的兴趣点分布应采用较大的带宽,而对于密集型的兴趣点则应考虑较小一些的带宽。
2.2.1 自适应或可变带宽的核密度估计
如果带宽不是固定的,而是根据样本的位置而变化(其变化取决于估计的位置(balloon estimator)或样本点(逐点估计pointwise estimator)),则会产生一种特别有力的方法,称为自适应或可变带宽的核密度估计。就POI兴趣点推荐来说,由于密集的城市地区的签到密度很高,人烟稀少的农村地区的签到密度较低。就是说不同位置应该采取不同的分析尺度,因此本文采用不固定的带宽来进行核密度估计。
说到这, 有些朋友可能不知道POI兴趣点推荐是啥意思, 这里简单的说一下:POI是Point-of-Interest的意思,即兴趣点。就是说,给用户推荐其感兴趣的地点。就这么简单。在推荐系统相关领域,兴趣点推荐是一个非常火爆的研究课题。这里会用到核密度估计的方法,比如这篇论文:Jia-Dong Zhang,Chi-Yin Chow.(2015)GeoSoCa: Exploiting Geographical, Social and Categorical Correlations for Point-of-Interest Recommendations.SIGIR’15, August 09 - 13, 2015, Santiago, Chile.就利用了可变带宽的核密度估计方法。
这里再简单讨论一下自适应带宽的核密度估计方法。自适应带宽的核密度估计方法是在固定带宽核密度函数的基础上,通过修正带宽参数为而得到的,其形式如式所示:
这里 k(x) 是带宽为 ![]() 的核密度估计函数,M 是样例的个数,看出来了吧,每一个点 j 都有一个带宽
的核密度估计函数,M 是样例的个数,看出来了吧,每一个点 j 都有一个带宽![]() ,因此这叫自适应或可变。K(x) 是核函数,这里用了高斯核函数,当然也可以是其他的核函数。0≤α≤1,为灵敏因子,通常 α 取0.5,α=0 时,自适应带宽的核密度估计就变成了固定带宽的核密度估计了。固定带宽的核密度估计就是前面说的核密度估计。ω 表示带宽的参数。
,因此这叫自适应或可变。K(x) 是核函数,这里用了高斯核函数,当然也可以是其他的核函数。0≤α≤1,为灵敏因子,通常 α 取0.5,α=0 时,自适应带宽的核密度估计就变成了固定带宽的核密度估计了。固定带宽的核密度估计就是前面说的核密度估计。ω 表示带宽的参数。
2.3 多维
还可以扩展到多维,即:
其中d为x的维数,K为多维的kernel,一般为d个一维kernel的乘积。
核密度估计 Kernel Density Estimation(KDE):https://blog.csdn.net/unixtch/article/details/78556499
核密度估计(Kernel density estimation):https://blog.csdn.net/yuanxing14/article/details/41948485
什么是核密度估计?如何感性认识?:https://www.zhihu.com/question/27301358/answer/105267357?from=profile_answer_card
核密度估计Kernel Density Estimation(KDE)概述 密度估计的问题:https://www.jianshu.com/p/428ae3658f85
自适应带宽的核密度估计可以参考维基百科:https://en.wikipedia.org/wiki/Variable_kernel_density_estimation