并查集(union-find)算法学习笔记
输入一列整数队,一对整数可以被理解为这整数两个对象是互相连接的,且其中每个对象都属于一个等价类,若两个对象直接相连或者间接相连时它们属于同一个等价类。
这样的等价关系能将这些整数分为多个等价类。
如图中所示,首先是0到9有10个互不关联的对象,有10个等价类。
首先输入(4,3),将4和3相连,此时4,3属于同一个等价类,此时有9个等价类。
输入(3,8),8加入4和3的等价类,此时等价类有8个。
输入(6,5),把6和5相连,此时6,5又属于一个新的等价类,此时有7个等价类。
输入(9,4),9加入(8,4,3)的等价类,此时等价类有6个。
输入(2,1),把2和1相连,此时1,2又属于新生成的一个等价类,此时有5个等价类。
输入(8,9),因为8和9已经在同一个等价类中了,所以不必再相连。此时有5个等价类。(避免生成环)
输入(5,0),0加入(5,6)的等价类,此时等价类有4个。
输入(7,2),7加入(1,2)的等价类,此时等价类有3个。
输入(6,1),将(1,2,7)等价类和(5,0,6)的等价类合并,此时等价类有2个。
输入(1,0),因为1和0已经在同一个等价类中了,所以不必再相连,此时有2个等价类。
输入(6,7),因为6和7已经在同一个等价类中了,所以不必再相连,此时有2个等价类。
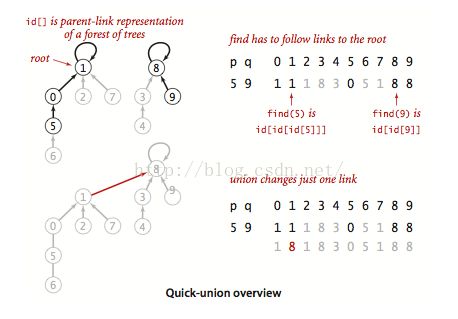
此时的这两个等价类会形成森林结构,发现每个等价类都会有一个根节点。若连接两个等价类的根节点便可以只剩1个等价类
这样就将不相关的10个数分为了2大类。如果再输入新的整数对,便可根据已知的等价类判断新的整数对是否相连:
如果输入(1,7),发现它们属于同一个等价类,则已经相连。
如果输入(1,8),发现它们属于不同的等价类,可以选择相连,这样等价类就变成了1个。
在最开始输入整数对时,可用数组来储存。下标表示这个整数对象,这个数组对象的值表示它属于哪一个等价类。
例: int id[9];用一个数组来储存这10个数
for(int i=0;i<=9;i++) {id[i]=i; }初始化分量id数组,刚开始时每个整数对象都单独的属于一个等价类,所以其值为它的下标.
在union-find中常用到的一些函数有:void union(int p ,int q) 这个函数实现在整数p和q间加一条连接.
int find (int p)这个函数实现找到整数对象属于哪一个等价类.
boolean connected(int p, int q)这个函数实现如果整数对象p和q属于同一个等价类,则返回true.
除这三个函数外,一般还会用一个整数对象保存当前等价类的个数:int count;
find函数的实现:
int find(int p){
while( p!=id[p]) p=id[p];找出p所属于等价类的根节点。
return p;
}
union函数的实现:
void union(int p, int q){
int pRoot=find(p);
int qRoot=find(q);
if(pRoot == qRoot) return; 根节点相同,表明属于同一个等价类,避免生成环
id[pRoot]=qRoot;建立连接,将两个等价类的根节点相连。
count --; 少了一个等价类。
}
connected函数的实现:
boolean connected(int p, int q) {return find(p)==find(q);}根节点相同则表明在同一等价类返回true。
此外还有加权quick-union算法,这里直接粘贴了,是用java实现的。
public class WeightedQuickUnionUF { private int[] parent; // parent[i] = parent of i private int[] size; // size[i] = number of sites in subtree rooted at i private int count; // number of components /** * Initializes an empty union–find data structure with {@code n} sites * {@code 0} through {@code n-1}. Each site is initially in its own * component. * * @param n the number of sites * @throws IllegalArgumentException if {@code n < 0} */ public WeightedQuickUnionUF(int n) { count = n; parent = new int[n]; size = new int[n]; for (int i = 0; i < n; i++) { parent[i] = i; size[i] = 1; } } /** * Returns the number of components. * * @return the number of components (between {@code 1} and {@code n}) */ public int count() { return count; } /** * Returns the component identifier for the component containing site {@code p}. * * @param p the integer representing one object * @return the component identifier for the component containing site {@code p} * @throws IllegalArgumentException unless {@code 0 <= p < n} */ public int find(int p) { validate(p); while (p != parent[p]) p = parent[p]; return p; } // validate that p is a valid index private void validate(int p) { int n = parent.length; if (p < 0 || p >= n) { throw new IllegalArgumentException("index " + p + " is not between 0 and " + (n-1)); } } /** * Returns true if the the two sites are in the same component. * * @param p the integer representing one site * @param q the integer representing the other site * @return {@code true} if the two sites {@code p} and {@code q} are in the same component; * {@code false} otherwise * @throws IllegalArgumentException unless * both {@code 0 <= p < n} and {@code 0 <= q < n} */ public boolean connected(int p, int q) { return find(p) == find(q); } /** * Merges the component containing site {@code p} with the * the component containing site {@code q}. * * @param p the integer representing one site * @param q the integer representing the other site * @throws IllegalArgumentException unless * both {@code 0 <= p < n} and {@code 0 <= q < n} */ public void union(int p, int q) { int rootP = find(p); int rootQ = find(q); if (rootP == rootQ) return; // make smaller root point to larger one if (size[rootP] < size[rootQ]) { parent[rootP] = rootQ; size[rootQ] += size[rootP]; }
else { parent[rootQ] = rootP; size[rootP] += size[rootQ]; } count--; } /** * Reads in a sequence of pairs of integers (between 0 and n-1) from standard input, * where each integer represents some object; * if the sites are in different components, merge the two components * and print the pair to standard output. * * @param args the command-line arguments */ public static void main(String[] args) { int n = StdIn.readInt(); WeightedQuickUnionUF uf = new WeightedQuickUnionUF(n); while (!StdIn.isEmpty()) { int p = StdIn.readInt(); int q = StdIn.readInt(); if (uf.connected(p, q)) continue; uf.union(p, q); StdOut.println(p + " " + q); } StdOut.println(uf.count() + " components"); } }
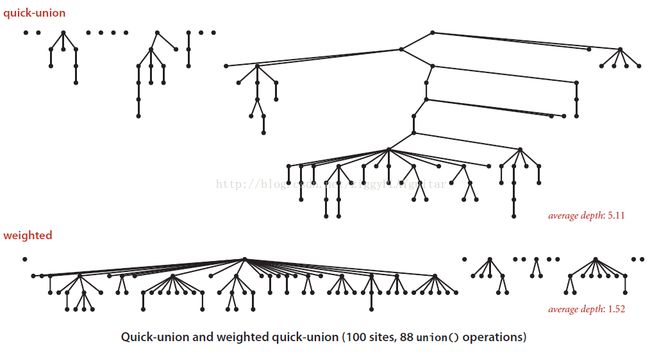
此外下面这张图是quick-union算法和加权 quick-union算法的对比
接下来是各种union-find算法的性能特点:
有一道编程题可以用到UF:
为了灌溉,雷雷需要建立一些水渠,以连接水井和麦田,雷雷也可以利用部分麦田作为“中转站”,利用水渠连接不同的麦田,这样只要一片麦田能被灌溉,则与其连接的麦田也能被灌溉。
现在雷雷知道哪些麦田之间可以建设水渠和建设每个水渠所需要的费用(注意不是所有麦田之间都可以建立水渠)。请问灌溉所有麦田最少需要多少费用来修建水渠。
接下来m行,每行包含三个整数a i, b i, c i,表示第a i片麦田与第b i片麦田之间可以建立一条水渠,所需要的费用为c i。
#include
#include
#include
using namespace std;
class UF{
private:
vectorv;
public:
UF(int n){
for (int i=0; i<=n; i++)
v.push_back(i);
}
int find(int x){
while (v[x]!=x)
x=v[x];
return x;
}
bool Union(int x,int y){
x=find(x);
y=find(y);
if (x==y)
return false;
else{
v[x]=y;
return true;
}
}
};
struct edge{
int s,d,cost;
bool operator < (const edge& n) const{
return cost>n.cost;
}
};
int main(){
priority_queueq;
edge e;
int n,m;
cin>>n>>m;
for (int i=1; i<=m; i++) {
cin>>e.s>>e.d>>e.cost;
q.push(e);
}
UF uf(n);
int ans=0,count=0;
while (count!=n-1) {
e=q.top();
q.pop();
if (!uf.Union(e.s, e.d))
continue;
else{
ans+=e.cost;
count++;
}
}
cout< 照着老师的方法写了一遍,有小改动。 老师的页面在这里