波士顿房价预测任务
构建波士顿房价预测任务的神经网络模型
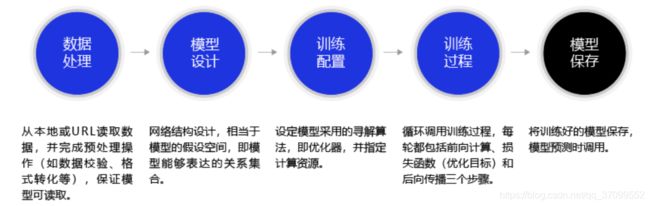
一、数据处理
数据处理包含五个部分:数据导入、数据形状变换、数据集划分、数据归一化处理和封装load data函数。数据预处理后,才能被模型调用。
- 读入数据:通过读入数据,了解波士顿房价的数据集结构。
- 数据形状变换:由于读入的原始数据是1维的,所有数据都连在一起。因此需要我们将数据的形状进行变换,形成一个2维的矩阵,每行为一个数据样本(14个值),每个数据样本包含13个X(影响房价的特征)和一个Y(该类型房屋的均价)。
- 划分数据集 :将数据集划分成训练集和测试集,其中训练集用于确定模型的参数,测试集用于评判模型的效果。
- 数据归一化处理:对每个特征进行归一化处理,使得每个特征的取值缩放到0~1之间。这样做有两个好处:一是模型训练更高效;二是特征前的权重大小可以代表该变量对预测结果的贡献度(因为每个特征值本身的范围相同)。
- 封装成load data函数:将上述几个数据处理操作封装成load data函数,以便下一步模型的调用。
def load_data():
# 从文件导入数据
datafile = './work/housing.data'
data = np.fromfile(datafile, sep=' ')
# 每条数据包括14项,其中前面13项是影响因素,第14项是相应的房屋价格中位数
feature_names = [ 'CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', \
'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV' ]
feature_num = len(feature_names)
# 将原始数据进行Reshape,变成[N, 14]这样的形状
data = data.reshape([data.shape[0] // feature_num, feature_num])
# 将原数据集拆分成训练集和测试集
# 这里使用80%的数据做训练,20%的数据做测试
# 测试集和训练集必须是没有交集的
ratio = 0.8
offset = int(data.shape[0] * ratio)
training_data = data[:offset]
# 计算训练集的最大值,最小值,平均值
maximums, minimums, avgs = training_data.max(axis=0), training_data.min(axis=0), \
training_data.sum(axis=0) / training_data.shape[0]
# 对数据进行归一化处理
for i in range(feature_num):
#print(maximums[i], minimums[i], avgs[i])
data[:, i] = (data[:, i] - minimums[i]) / (maximums[i] - minimums[i])
# 训练集和测试集的划分比例
training_data = data[:offset]
test_data = data[offset:]
return training_data, test_data
# 获取数据
training_data, test_data = load_data()
x = training_data[:, :-1]
y = training_data[:, -1:]
# 查看数据
print(x[0])
print(y[0])
二、模型设计
模型设计是深度学习模型关键要素之一,也称为网络结构设计,相当于模型的假设空间,即实现模型“前向计算”(从输入到输出)的过程。将计算预测输出的过程以“类和对象”的方式来描述,类成员变量有参数w和b。通过写一个forward函数(代表“前向计算”)完成上述从特征和参数到输出预测值的计算过程
class Network(object):
def __init__(self, num_of_weights):
# 随机产生w的初始值
# 为了保持程序每次运行结果的一致性,
# 此处设置固定的随机数种子
np.random.seed(0)
self.w = np.random.randn(num_of_weights, 1)
self.b = 0.
def forward(self, x):
z = np.dot(x, self.w) + self.b
return z
基于Network类的定义,模型的计算过程如下所示。
net = Network(13)
x1 = x[0]
y1 = y[0]
z = net.forward(x1)
print(z)
三、训练配置
模型设计完成后,需要通过训练配置寻找模型的最优值,即通过损失函数来衡量模型的好坏。训练配置也是深度学习模型关键要素之一
Loss = ( y − z ) 2 \operatorname{Loss}=(y-z)^{2} Loss=(y−z)2
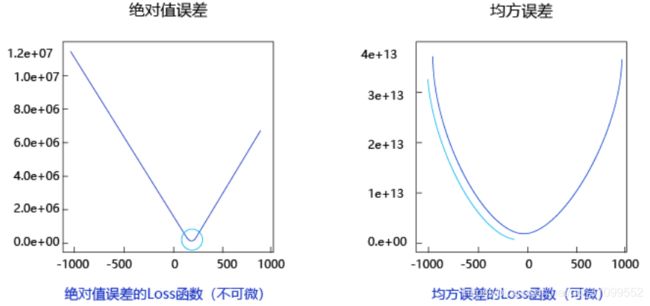
它是衡量模型好坏的指标。在回归问题中均方误差是一种比较常见的形式,分类问题中通常会采用交叉熵作为损失函数。因为计算损失函数时需要把每个样本的损失函数值都考虑到,所以我们需要对单个样本的损失函数进行求和
Los s = 1 N ∑ i = 1 N ( y i − z i ) 2 \operatorname{Los} s=\frac{1}{N} \sum_{i=1}^{N}\left(y_{i}-z_{i}\right)^{2} Loss=N1i=1∑N(yi−zi)2
class Network(object):
def __init__(self, num_of_weights):
# 随机产生w的初始值
# 为了保持程序每次运行结果的一致性,此处设置固定的随机数种子
np.random.seed(0)
self.w = np.random.randn(num_of_weights, 1)
self.b = 0.
def forward(self, x):
z = np.dot(x, self.w) + self.b
return z
def loss(self, z, y):
error = z - y
cost = error * error
cost = np.mean(cost)
return cost
四、训练过程
上述计算过程描述了如何构建神经网络,通过神经网络完成预测值和损失函数的计算。接下来介绍如何求解参数w和b的数值,这个过程也称为模型训练过程。训练过程是深度学习模型的关键要素之一,其目标是让定义的损失函数Loss尽可能的小,也就是说找到一个参数解w和b使得损失函数取得极小值。
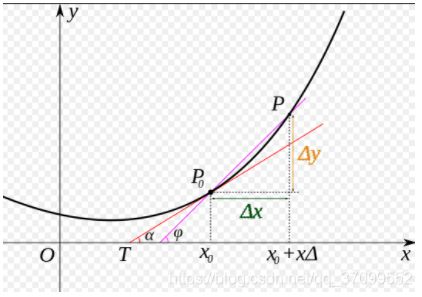
梯度下降法
从当前的参数取值,一步步的按照下坡的方向下降,直到走到最低点
net = Network(13)
losses = []
#只画出参数w5和w9在区间[-160, 160]的曲线部分,以及包含损失函数的极值
w5 = np.arange(-160.0, 160.0, 1.0)
w9 = np.arange(-160.0, 160.0, 1.0)
losses = np.zeros([len(w5), len(w9)])
#计算设定区域内每个参数取值所对应的Loss
for i in range(len(w5)):
for j in range(len(w9)):
net.w[5] = w5[i]
net.w[9] = w9[j]
z = net.forward(x)
loss = net.loss(z, y)
losses[i, j] = loss
#使用matplotlib将两个变量和对应的Loss作3D图
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = Axes3D(fig)
w5, w9 = np.meshgrid(w5, w9)
ax.plot_surface(w5, w9, losses, rstride=1, cstride=1, cmap='rainbow')
plt.show()
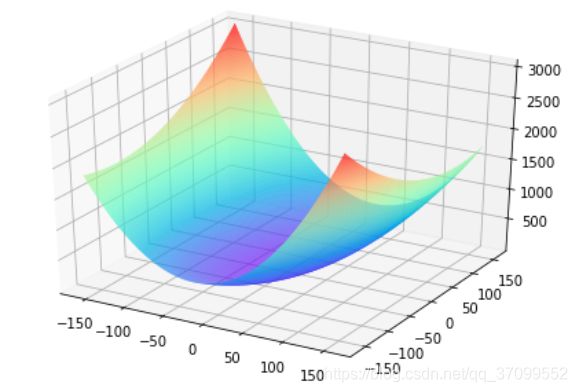
对于这种简单情形,我们利用上面的程序,可以在三维空间中画出损失函数随参数变化的曲面图。从图中可以看出有些区域的函数值明显比周围的点小。观察上述曲线呈现出“圆滑”的坡度,这正是我们选择以均方误差作为损失函数的原因之一。
将计算w和b的梯度的过程,写成Network类的gradient函数
class Network(object):
def __init__(self, num_of_weights):
# 随机产生w的初始值
# 为了保持程序每次运行结果的一致性,此处设置固定的随机数种子
np.random.seed(0)
self.w = np.random.randn(num_of_weights, 1)
self.b = 0.
def forward(self, x):
z = np.dot(x, self.w) + self.b
return z
def loss(self, z, y):
error = z - y
num_samples = error.shape[0]
cost = error * error
cost = np.sum(cost) / num_samples
return cost
def gradient(self, x, y):
z = self.forward(x)
gradient_w = (z-y)*x
gradient_w = np.mean(gradient_w, axis=0)
gradient_w = gradient_w[:, np.newaxis]
gradient_b = (z - y)
gradient_b = np.mean(gradient_b)
return gradient_w, gradient_b
确定损失函数更小的点
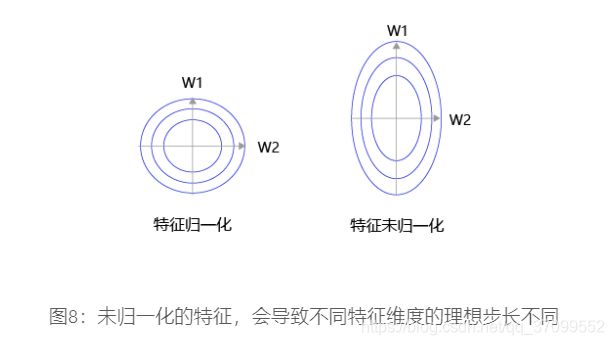
特征输入归一化后,不同参数输出的Loss是一个比较规整的曲线,学习率可以设置成统一的值 ;特征输入未归一化时,不同特征对应的参数所需的步长不一致,尺度较大的参数需要大步长,尺寸较小的参数需要小步长,导致无法设置统一的学习率。
五、代码封装Train函数
import numpy as np
class Network(object):
def __init__(self, num_of_weights):
# 随机产生w的初始值
# 为了保持程序每次运行结果的一致性,此处设置固定的随机数种子
#np.random.seed(0)
self.w = np.random.randn(num_of_weights, 1)
self.b = 0.
def forward(self, x):
z = np.dot(x, self.w) + self.b
return z
def loss(self, z, y):
error = z - y
num_samples = error.shape[0]
cost = error * error
cost = np.sum(cost) / num_samples
return cost
def gradient(self, x, y):
z = self.forward(x)
N = x.shape[0]
gradient_w = 1. / N * np.sum((z-y) * x, axis=0)
gradient_w = gradient_w[:, np.newaxis]
gradient_b = 1. / N * np.sum(z-y)
return gradient_w, gradient_b
def update(self, gradient_w, gradient_b, eta = 0.01):
self.w = self.w - eta * gradient_w
self.b = self.b - eta * gradient_b
def train(self, training_data, num_epoches, batch_size=10, eta=0.01):
n = len(training_data)
losses = []
for epoch_id in range(num_epoches):
# 在每轮迭代开始之前,将训练数据的顺序随机打乱
# 然后再按每次取batch_size条数据的方式取出
np.random.shuffle(training_data)
# 将训练数据进行拆分,每个mini_batch包含batch_size条的数据
mini_batches = [training_data[k:k+batch_size] for k in range(0, n, batch_size)]
for iter_id, mini_batch in enumerate(mini_batches):
#print(self.w.shape)
#print(self.b)
x = mini_batch[:, :-1]
y = mini_batch[:, -1:]
a = self.forward(x)
loss = self.loss(a, y)
gradient_w, gradient_b = self.gradient(x, y)
self.update(gradient_w, gradient_b, eta)
losses.append(loss)
print('Epoch {:3d} / iter {:3d}, loss = {:.4f}'.
format(epoch_id, iter_id, loss))
return losses
# 获取数据
train_data, test_data = load_data()
# 创建网络
net = Network(13)
# 启动训练
losses = net.train(train_data, num_epoches=50, batch_size=100, eta=0.1)
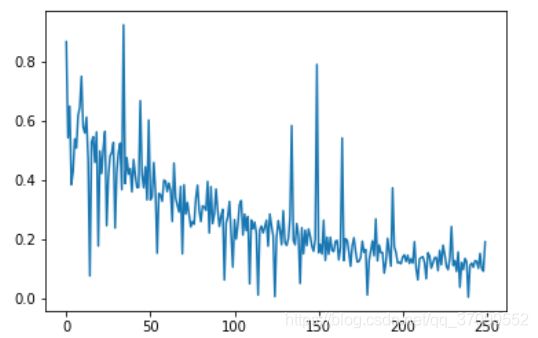
# 画出损失函数的变化趋势
plot_x = np.arange(len(losses))
plot_y = np.array(losses)
plt.plot(plot_x, plot_y)
plt.show()
Epoch 0 / iter 0, loss = 0.8668
Epoch 0 / iter 1, loss = 0.5423
Epoch 0 / iter 2, loss = 0.6492
Epoch 0 / iter 3, loss = 0.3843
Epoch 0 / iter 4, loss = 0.4286
Epoch 1 / iter 0, loss = 0.5387
Epoch 1 / iter 1, loss = 0.5079
Epoch 1 / iter 2, loss = 0.6171
Epoch 1 / iter 3, loss = 0.6461
Epoch 1 / iter 4, loss = 0.7498
Epoch 2 / iter 0, loss = 0.5787
Epoch 2 / iter 1, loss = 0.5588
Epoch 2 / iter 2, loss = 0.6120
Epoch 2 / iter 3, loss = 0.4652
Epoch 2 / iter 4, loss = 0.0764
Epoch 3 / iter 0, loss = 0.5283
Epoch 3 / iter 1, loss = 0.5461
Epoch 3 / iter 2, loss = 0.4598
Epoch 3 / iter 3, loss = 0.5620
Epoch 3 / iter 4, loss = 0.1775
Epoch 4 / iter 0, loss = 0.4977
Epoch 4 / iter 1, loss = 0.4221
Epoch 4 / iter 2, loss = 0.5079
Epoch 4 / iter 3, loss = 0.5639
Epoch 4 / iter 4, loss = 0.2461
Epoch 5 / iter 0, loss = 0.4102
Epoch 5 / iter 1, loss = 0.4805
Epoch 5 / iter 2, loss = 0.4926
Epoch 5 / iter 3, loss = 0.5262
Epoch 5 / iter 4, loss = 0.2380
Epoch 6 / iter 0, loss = 0.4288
Epoch 6 / iter 1, loss = 0.4934
Epoch 6 / iter 2, loss = 0.5244
Epoch 6 / iter 3, loss = 0.3675
Epoch 6 / iter 4, loss = 0.9236
Epoch 7 / iter 0, loss = 0.3882
Epoch 7 / iter 1, loss = 0.4751
Epoch 7 / iter 2, loss = 0.4198
Epoch 7 / iter 3, loss = 0.4381
Epoch 7 / iter 4, loss = 0.3601
Epoch 8 / iter 0, loss = 0.4693
Epoch 8 / iter 1, loss = 0.4167
Epoch 8 / iter 2, loss = 0.3746
Epoch 8 / iter 3, loss = 0.3753
Epoch 8 / iter 4, loss = 0.6677
Epoch 9 / iter 0, loss = 0.4195
Epoch 9 / iter 1, loss = 0.3744
Epoch 9 / iter 2, loss = 0.4447
Epoch 9 / iter 3, loss = 0.3329
Epoch 9 / iter 4, loss = 0.6023
Epoch 10 / iter 0, loss = 0.3330
Epoch 10 / iter 1, loss = 0.3435
Epoch 10 / iter 2, loss = 0.4590
Epoch 10 / iter 3, loss = 0.3632
Epoch 10 / iter 4, loss = 0.1531
Epoch 11 / iter 0, loss = 0.3545
Epoch 11 / iter 1, loss = 0.3494
Epoch 11 / iter 2, loss = 0.3286
Epoch 11 / iter 3, loss = 0.3993
Epoch 11 / iter 4, loss = 0.3965
Epoch 12 / iter 0, loss = 0.3612
Epoch 12 / iter 1, loss = 0.3894
Epoch 12 / iter 2, loss = 0.3650
Epoch 12 / iter 3, loss = 0.2601
Epoch 12 / iter 4, loss = 0.4570
Epoch 13 / iter 0, loss = 0.3388
Epoch 13 / iter 1, loss = 0.3147
Epoch 13 / iter 2, loss = 0.2922
Epoch 13 / iter 3, loss = 0.3782
Epoch 13 / iter 4, loss = 0.1508
Epoch 14 / iter 0, loss = 0.3840
Epoch 14 / iter 1, loss = 0.2851
Epoch 14 / iter 2, loss = 0.3241
Epoch 14 / iter 3, loss = 0.2832
Epoch 14 / iter 4, loss = 0.2419
Epoch 15 / iter 0, loss = 0.2598
Epoch 15 / iter 1, loss = 0.2507
Epoch 15 / iter 2, loss = 0.3381
Epoch 15 / iter 3, loss = 0.3823
Epoch 15 / iter 4, loss = 0.2972
Epoch 16 / iter 0, loss = 0.2597
Epoch 16 / iter 1, loss = 0.3126
Epoch 16 / iter 2, loss = 0.3093
Epoch 16 / iter 3, loss = 0.2979
Epoch 16 / iter 4, loss = 0.3951
Epoch 17 / iter 0, loss = 0.2211
Epoch 17 / iter 1, loss = 0.3773
Epoch 17 / iter 2, loss = 0.2532
Epoch 17 / iter 3, loss = 0.2847
Epoch 17 / iter 4, loss = 0.3696
Epoch 18 / iter 0, loss = 0.2974
Epoch 18 / iter 1, loss = 0.2432
Epoch 18 / iter 2, loss = 0.2769
Epoch 18 / iter 3, loss = 0.3010
Epoch 18 / iter 4, loss = 0.0626
Epoch 19 / iter 0, loss = 0.2549
Epoch 19 / iter 1, loss = 0.2765
Epoch 19 / iter 2, loss = 0.3274
Epoch 19 / iter 3, loss = 0.2175
Epoch 19 / iter 4, loss = 0.1061
Epoch 20 / iter 0, loss = 0.2658
Epoch 20 / iter 1, loss = 0.2009
Epoch 20 / iter 2, loss = 0.2497
Epoch 20 / iter 3, loss = 0.3171
Epoch 20 / iter 4, loss = 0.3303
Epoch 21 / iter 0, loss = 0.2144
Epoch 21 / iter 1, loss = 0.2849
Epoch 21 / iter 2, loss = 0.2292
Epoch 21 / iter 3, loss = 0.2764
Epoch 21 / iter 4, loss = 0.0497
Epoch 22 / iter 0, loss = 0.2648
Epoch 22 / iter 1, loss = 0.2353
Epoch 22 / iter 2, loss = 0.2576
Epoch 22 / iter 3, loss = 0.2183
Epoch 22 / iter 4, loss = 0.0116
Epoch 23 / iter 0, loss = 0.2312
Epoch 23 / iter 1, loss = 0.2444
Epoch 23 / iter 2, loss = 0.2215
Epoch 23 / iter 3, loss = 0.2414
Epoch 23 / iter 4, loss = 0.2644
Epoch 24 / iter 0, loss = 0.1768
Epoch 24 / iter 1, loss = 0.2853
Epoch 24 / iter 2, loss = 0.2454
Epoch 24 / iter 3, loss = 0.2114
Epoch 24 / iter 4, loss = 0.0068
Epoch 25 / iter 0, loss = 0.2041
Epoch 25 / iter 1, loss = 0.2629
Epoch 25 / iter 2, loss = 0.2315
Epoch 25 / iter 3, loss = 0.1815
Epoch 25 / iter 4, loss = 0.2964
Epoch 26 / iter 0, loss = 0.1892
Epoch 26 / iter 1, loss = 0.1794
Epoch 26 / iter 2, loss = 0.2017
Epoch 26 / iter 3, loss = 0.2716
Epoch 26 / iter 4, loss = 0.5838
Epoch 27 / iter 0, loss = 0.1968
Epoch 27 / iter 1, loss = 0.1814
Epoch 27 / iter 2, loss = 0.2526
Epoch 27 / iter 3, loss = 0.2123
Epoch 27 / iter 4, loss = 0.0509
Epoch 28 / iter 0, loss = 0.2392
Epoch 28 / iter 1, loss = 0.1510
Epoch 28 / iter 2, loss = 0.2306
Epoch 28 / iter 3, loss = 0.1788
Epoch 28 / iter 4, loss = 0.2348
Epoch 29 / iter 0, loss = 0.2119
Epoch 29 / iter 1, loss = 0.1772
Epoch 29 / iter 2, loss = 0.1594
Epoch 29 / iter 3, loss = 0.1999
Epoch 29 / iter 4, loss = 0.7900
Epoch 30 / iter 0, loss = 0.1545
Epoch 30 / iter 1, loss = 0.1820
Epoch 30 / iter 2, loss = 0.1500
Epoch 30 / iter 3, loss = 0.2641
Epoch 30 / iter 4, loss = 0.1289
Epoch 31 / iter 0, loss = 0.2068
Epoch 31 / iter 1, loss = 0.1495
Epoch 31 / iter 2, loss = 0.2068
Epoch 31 / iter 3, loss = 0.1619
Epoch 31 / iter 4, loss = 0.1587
Epoch 32 / iter 0, loss = 0.1933
Epoch 32 / iter 1, loss = 0.1959
Epoch 32 / iter 2, loss = 0.1305
Epoch 32 / iter 3, loss = 0.1719
Epoch 32 / iter 4, loss = 0.5420
Epoch 33 / iter 0, loss = 0.1284
Epoch 33 / iter 1, loss = 0.2014
Epoch 33 / iter 2, loss = 0.1963
Epoch 33 / iter 3, loss = 0.1578
Epoch 33 / iter 4, loss = 0.1088
Epoch 34 / iter 0, loss = 0.1777
Epoch 34 / iter 1, loss = 0.2050
Epoch 34 / iter 2, loss = 0.1590
Epoch 34 / iter 3, loss = 0.1230
Epoch 34 / iter 4, loss = 0.1253
Epoch 35 / iter 0, loss = 0.1383
Epoch 35 / iter 1, loss = 0.1932
Epoch 35 / iter 2, loss = 0.1563
Epoch 35 / iter 3, loss = 0.1654
Epoch 35 / iter 4, loss = 0.0118
Epoch 36 / iter 0, loss = 0.1283
Epoch 36 / iter 1, loss = 0.1597
Epoch 36 / iter 2, loss = 0.1941
Epoch 36 / iter 3, loss = 0.1441
Epoch 36 / iter 4, loss = 0.2685
Epoch 37 / iter 0, loss = 0.1274
Epoch 37 / iter 1, loss = 0.1804
Epoch 37 / iter 2, loss = 0.1551
Epoch 37 / iter 3, loss = 0.1545
Epoch 37 / iter 4, loss = 0.0857
Epoch 38 / iter 0, loss = 0.1210
Epoch 38 / iter 1, loss = 0.2029
Epoch 38 / iter 2, loss = 0.1555
Epoch 38 / iter 3, loss = 0.1093
Epoch 38 / iter 4, loss = 0.3734
Epoch 39 / iter 0, loss = 0.1744
Epoch 39 / iter 1, loss = 0.1560
Epoch 39 / iter 2, loss = 0.1203
Epoch 39 / iter 3, loss = 0.1229
Epoch 39 / iter 4, loss = 0.1174
Epoch 40 / iter 0, loss = 0.1401
Epoch 40 / iter 1, loss = 0.1472
Epoch 40 / iter 2, loss = 0.1249
Epoch 40 / iter 3, loss = 0.1461
Epoch 40 / iter 4, loss = 0.1185
Epoch 41 / iter 0, loss = 0.1338
Epoch 41 / iter 1, loss = 0.1199
Epoch 41 / iter 2, loss = 0.1915
Epoch 41 / iter 3, loss = 0.1001
Epoch 41 / iter 4, loss = 0.0632
Epoch 42 / iter 0, loss = 0.1339
Epoch 42 / iter 1, loss = 0.1380
Epoch 42 / iter 2, loss = 0.1410
Epoch 42 / iter 3, loss = 0.1205
Epoch 42 / iter 4, loss = 0.0668
Epoch 43 / iter 0, loss = 0.1542
Epoch 43 / iter 1, loss = 0.1429
Epoch 43 / iter 2, loss = 0.1025
Epoch 43 / iter 3, loss = 0.1204
Epoch 43 / iter 4, loss = 0.1380
Epoch 44 / iter 0, loss = 0.1381
Epoch 44 / iter 1, loss = 0.0939
Epoch 44 / iter 2, loss = 0.1621
Epoch 44 / iter 3, loss = 0.1140
Epoch 44 / iter 4, loss = 0.1799
Epoch 45 / iter 0, loss = 0.1486
Epoch 45 / iter 1, loss = 0.1090
Epoch 45 / iter 2, loss = 0.0974
Epoch 45 / iter 3, loss = 0.1341
Epoch 45 / iter 4, loss = 0.2428
Epoch 46 / iter 0, loss = 0.1116
Epoch 46 / iter 1, loss = 0.1281
Epoch 46 / iter 2, loss = 0.0916
Epoch 46 / iter 3, loss = 0.1570
Epoch 46 / iter 4, loss = 0.0379
Epoch 47 / iter 0, loss = 0.1215
Epoch 47 / iter 1, loss = 0.0976
Epoch 47 / iter 2, loss = 0.1352
Epoch 47 / iter 3, loss = 0.1245
Epoch 47 / iter 4, loss = 0.0049
Epoch 48 / iter 0, loss = 0.1111
Epoch 48 / iter 1, loss = 0.1195
Epoch 48 / iter 2, loss = 0.1058
Epoch 48 / iter 3, loss = 0.1276
Epoch 48 / iter 4, loss = 0.1252
Epoch 49 / iter 0, loss = 0.1020
Epoch 49 / iter 1, loss = 0.1521
Epoch 49 / iter 2, loss = 0.1011
Epoch 49 / iter 3, loss = 0.0926
Epoch 49 / iter 4, loss = 0.1909