这是我见过讲解最详细最通俗易懂的决策树(二)
这是我见过讲解最详细最通俗易懂的决策树(二)
- 增益率
- 基尼指数
- 剪枝处理
- 预剪枝
- 后剪枝
我们在上一篇博文里面介绍了决策树的概念,讲到了什么是决策树,讲到了如何划分选择、讲到了何为信息增益等。今天我们继续之前的话题,首先讲解一下增益率。
如果您对上一篇博客的内容有所遗忘,请点击下面的连接
这是我见过讲解最详细最通俗易懂的决策树(一)
增益率
废话不多说,我们先把数据集拿出来。
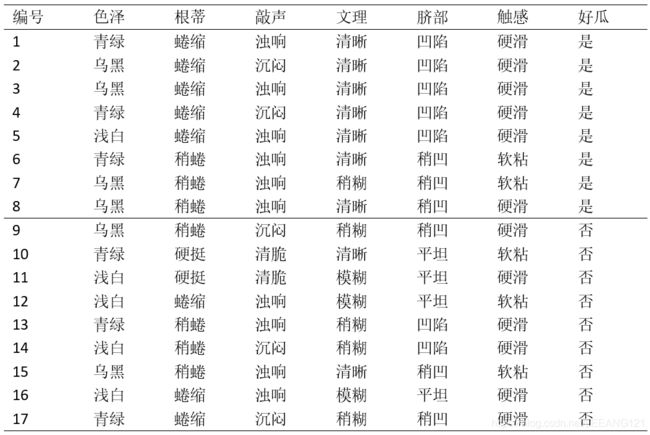
在之前介绍信息增益的时候,我们并没有考虑过这个数据集中的’编号‘。现在假如我们把编号也作为一个候选进行属性划分,那么根据前一篇文章的公式2(这里公式再写一下):
G a i n ( D , a ) = E n t ( D ) − ∑ v = 1 V D v D E n t ( D v ) Gain(D,a)=Ent(D)-\sum_{v=1}^{V}\frac{D^{v}}{D}Ent(D^{v}) Gain(D,a)=Ent(D)−∑v=1VDDvEnt(Dv)
我们得到信息增益为0.998.远大于其他候选划分属性。这很容易理解,‘编号’会产生17个分支,这里就是所有的分支,每个分支仅包含一个样本,这些分支结点的纯度已经最大。不过这个决策树也有一个致命缺陷,就是不具备泛化能力。也就是我们在优化算法里面提到的,这颗树过拟合了。
实际上,信息增益准则对可取值数目较多的属性有所偏好,为了减少这种偏好可能带来的不利影响,注明的C4.5决策树算法不直接采用信息增益,而是使用增益率来选择最优划分属性,采用公式2相同的符号表示,增益率定义为:
G a i n r a t i o n ( D , a ) = G a i n ( D , a ) I V ( a ) Gain_ration(D,a)=\frac{Gain(D,a)}{IV(a)} Gainration(D,a)=IV(a)Gain(D,a)------------------------------------------------------------公式3
其中, I V ( a ) = − ∑ v = 1 V ∣ D v ∣ ∣ D ∣ l o g 2 ∣ D v ∣ ∣ D ∣ IV(a)=-\sum_{v=1}^{V}\frac{\left | D^{v} \right |}{\left | D \right |}log_{2}\frac{\left | D^{v} \right |}{\left | D \right |} IV(a)=−∑v=1V∣D∣∣Dv∣log2∣D∣∣Dv∣-----------------------------------------------------公式4
属性 a a a称为‘固有值’,属性 a a a的可能取值数目越多(即 V V V越大),则 I V ( a ) IV(a) IV(a)的值通常会越大。例如,对于上面西瓜数据集, I V ( 触 感 ) = 0.874 ( V = 2 ) IV(触感)=0.874(V=2) IV(触感)=0.874(V=2), I V ( 色 泽 ) = 1.580 ( V = 3 ) IV(色泽)=1.580(V=3) IV(色泽)=1.580(V=3), I V ( 编 号 ) = 4.08 ( V = 17 ) IV(编号)=4.08(V=17) IV(编号)=4.08(V=17).
从上面的结果可以看出,增益率准则对可取数目较少的属性有所偏好,因此C4.5算法并不是直接选择增益率最大的时候划分属性,而是使用了一个启发式算法:先从候选划分属性找出信息增益高于平均水平的属性,再从中选择增益率最高的。
基尼指数
CART决策树使用‘基尼指数’来选择划分属性,采用与公式上一篇博文公式1相同的符号(我们先来回顾一下该公式: E n t ( D ) = − ∑ k = 1 ∣ y ∣ p k l o g 2 p k Ent(D)=-\sum_{k=1}^{\left | y \right |}p_{k}log_{2}p_{k} Ent(D)=−∑k=1∣y∣pklog2pk)
数据集 D D D的纯度可以用基尼值来度量:
G i n i ( D ) = ∑ k = 1 ∣ y ∣ ∑ k ′ ≠ k p k p k ′ = 1 − ∑ k = 1 ∣ y ∣ p k 2 Gini(D)=\sum_{k=1}^{\left | y \right |}\sum_{k^{'}\neq k}p_{k}p_{k^{'}}=1-\sum_{k=1}^{\left | y \right |}p_{k}^{2} Gini(D)=∑k=1∣y∣∑k′=kpkpk′=1−∑k=1∣y∣pk2---------------------------------------公式5
直观来说, G i n i ( D ) Gini(D) Gini(D)反映了从数据集D中随机抽取两个样本,其类别标记不一致的概率,因此 G i n i ( D ) Gini(D) Gini(D)越小,则数据集 D D D的纯度越高。
属性 a a a的基尼指数定义为:
G i n i i n d e x ( D , a ) = ∑ v = 1 V ∣ D v ∣ ∣ D ∣ G i n i ( D v ) Gini_index(D,a)=\sum_{v=1}^{V}\frac{\left | D^{v} \right |}{\left | D \right |}Gini(D^{v}) Giniindex(D,a)=∑v=1V∣D∣∣Dv∣Gini(Dv)
我们在候选属性集合 A A A中,选择哪个使得划分后基尼指数最小的属性作为最优划分属性,即
a ∗ = a r g m i n a ∈ A G i n i i n d e x ( D , a ) a_{*}=\underset{a\in A}{argmin} Gini_index(D,a) a∗=a∈AargminGiniindex(D,a)
剪枝处理
剪枝处理,顾名思义,就是把决策树的树枝修理剪裁。这个是不是类似我们之前在讲CNN卷积神经网络时提到的dropout?那么剪枝处理是干嘛的呢?防止过拟合。
剪枝处理的基本策略可以分为‘预剪枝’和‘后剪枝’两种。不论采取哪种方式,最终的目的是为了提高泛化性。那么问题来了,如何判断泛化性是否提高?
我们这里采用‘留出法’,即预留一部分数据作为‘验证集’以进行性能评估。首先我们先来修改一下我们的西瓜数据集(双线上部分为训练集、双线下部分为验证集):

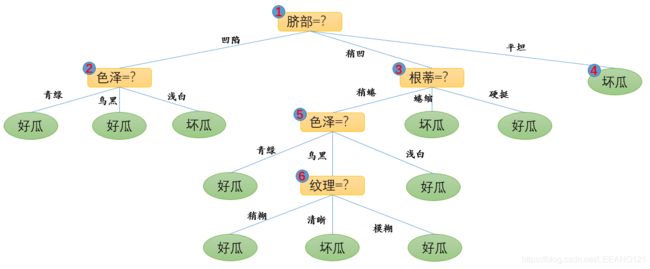
我们采用上一篇博文提到的信息增益进行属性划分,得到的决策树如下图所示(图1):
这里对这颗树做一个简单的解释:
1,为什么以‘脐部’作为根结点?
这是由于我们之前通过计算,‘脐部’的信息增益最高。(与根蒂、触感并列第一)
2,为什么‘脐部’划分平坦后,直接得到坏瓜?
这个我们要参考上表,我们可以发现,以脐部为跟结点的情况下,’凹陷‘特征和’稍凹‘特征均可以分化出两个结果(我们这里看的是训练集),平坦这个特征仅对应坏瓜的叶节点。
3,’脐部‘–’凹陷‘–色泽下面对应的三个属性如何判别叶节点?
我们还是在训练集里面找特征,首先凹陷的脐部对应的青绿有一个好瓜,我们将属性定义为好瓜,同理乌黑对应2个好瓜,我们将属性定义为好瓜,但是浅白这个特征对应一个坏瓜,因此最后我们定义为坏瓜。
预剪枝
我们先讨论‘预剪枝’,基于信息增益准则,我们选取属性‘脐部’来对训练集进行划分,并产生三个分支。如图所示:
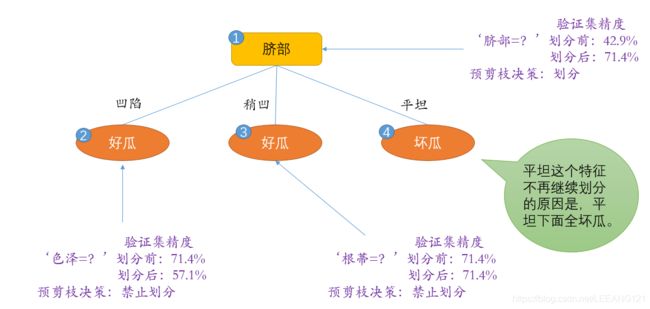
正如我们上面提到的,我们通过判断剪裁前后的变化决定是否剪裁。在本例中,再划分之前,所有样例集中在根结点。若不进行划分,我们可以将结点标记为叶结点,其类别标记为训练样例最多的类别,假设我们将这个结点标记为‘好瓜’,利用上表的验证集对这个单结点决策树进行评估,则编号为{4,5,8}的样例被分类为正确,另外4个样例被分类为错误。于是验证集精度为$3/7=0.429%.
用属性‘脐部’划分之后,上图中的结点2,结点3和结点4分别包含编号为{1,2,3,14}、{6,7,15,17}、{10,16}的训练样例,因此这3个结点分别被标记为叶节点‘好瓜’、‘好瓜’、‘坏瓜’。此时,验证集中编号为{4,5,8,11,12}的样例被分类正确(这里的分类正确是指,4,5,8正确判断为好瓜,11和12正确判断为坏瓜,下面的分类均为这个意思),验证精度为 5 / 7 = 0.714 5/7=0.714 5/7=0.714> 0.429 0.429 0.429,于是,用’脐部‘进行划分得意确定。
接下来,决策树算法应该对结点2进行划分,基于信息增益准则将挑选出划分属性‘色泽’,在使用‘色泽’划分后,编号为{5}的验证集样本分类结果会由正确转为错误,使得验证集精度下降为57.1% 。于是,预剪枝策略将禁止结点2被划分。
我们再看结点3,最优划分属性为‘根蒂’,划分后验证集精度仍然为71.4%。这个划分不能提高验证集精度,于是,预剪枝策略禁止结点3被划分。
对于结点4,其所包含的训练样例属于同一类,不再进行划分。
于是,基于预剪枝策略从上表数据生成的决策树如上图所示,验证集精度为71.4%。这是一颗仅有一层划分的决策树,也叫‘决策树桩’。
tips
对比上面两幅决策树的图可以发现,预剪枝使得很多分支没有展开,这样能有效减小过拟合的风险。但是另一方面,有些分支虽然当前不能提高泛化能力,甚至降低泛化能力,但是在其基础上的后续划分却有可能显著提高泛化能力,预剪枝基于‘贪心’本质禁止这些分支展开,又会带来欠拟合的风险。
后剪枝
后剪枝与预剪枝正好相反,后剪枝我们先生成一颗完整的树,然后从末端考察各个结点。若将该节点去掉可以提高泛化性能,则剪去该枝丫,否则保留。
我们先考察图1的结点6,若将其剪除,相当于将6替换为叶节点。替换后的叶节点包含编号为{7,15}的训练样本,于是,该叶节点被标记为‘好瓜’,此时决策树的验证精度提高至57.1%(原本的验证集精度为42.9%)。
说明一下{7,15}是如何选出来的,这两个属性要求同时满足脐部特征稍凹,并且根部稍蜷,并且是乌黑。以下选择原理相同。
现在后剪枝决策树如下图所示:
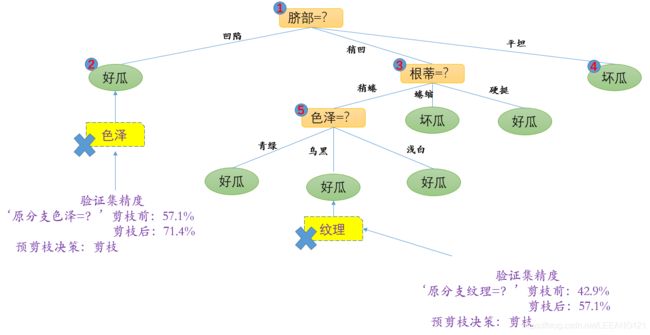
现在我们考察结点5,若将结点5去除,根据上面的思路,替换后叶节点包含的编号为{6,7,15}的训练样例,叶节点类别标记为‘好瓜’,此时决策树验证集精度仍然是57.1%,于是,可以不进行剪枝。
对结点2采用相同操作,替换后叶节点包含编号为{1,2,3,14},叶节点标记为‘好瓜’,此时决策树的验证集精度提高至71.4%,于是后剪枝策略决定剪枝。
对结点3和1,进行上述操作后,验证集精度分别为71.4%和42.9%,均未得到提高,于是他们被保留。
最终得到的决策树如上图所示。
对比上面两个图,后剪枝决策树通常比预剪枝决策树保留了更多的分支,一般情况下,后剪枝决策树的欠拟合风险很小,泛化性能优于预剪枝决策树。但是后剪枝决策树实在完全生成决策树之后进行,并且自底向上地对树中所有非叶节点进行逐一考察,因此训练时间比未剪枝决策树和预剪枝决策树都要大很多。
总结:
本章主要介绍了决策树的一些优化方法及特点。
下面一篇文章,我们会详细介绍如何处理连续与缺失值的问题及多变量决策树问题。
如果本文能对大家有那么一丁点帮助,本人不胜感激。
本文内容来自周志华的机器学习。
最后感谢郭老师的不理赐教。