浅尝则止 - SciPy科学计算
21. 浅尝则止 - SciPy科学计算
SciPy以NumPy为基础,提供了众多数学、科学、工程计算用的模块,包括但不限于:线性代数、常微分方程求解、信号处理、图像处理、稀疏矩阵处理。
本章适合那些有较好高等数学、线性代数、概率论基础的工科学生或从业者阅读。其他读者可以跳过,不影响后续章节。为减轻“数学恐惧症”患者的恐惧,作者尽量选择相对容易的“数学”案例来进行解读。
版权声明
本文可以在互联网上自由转载,但必须:注明出处(作者:海洋饼干叔叔)并包含指向本页面的链接。
本文不可以以纸质出版为目的进行改编、摘抄。
本文节选自作者的《Python编程基础及应用》视频教程。
21.1 常数
scipy.constants包含了众多的物理常数。
#Constants.py
from scipy import constants as C
print("c =",C.c) #光在真空中的传播速度
print("g =",C.g) #重力常数
执行结果
c= 299792458.0
g= 9.80665
其中,physical_constants是一个字典,它以物理常量名为键,对应值为一个三元素元组,分别是常数值、单位以及误差。下述程序可以打印其中的全部物理常数。下述程序执行结果中的electron volt常数表明了电子伏特与焦耳的换算关系。
#EnumConstants.py
from scipy import constants as C
for k,v in C.physical_constants.items():
print(k,v)
执行结果
...
electron volt (1.6021766208e-19, 'J', 9.8e-28)
...
constants模块还可以帮助进行单位转换,其中的单位转换常量可将英制单位以及公制非标准单位全部转换成公制标准单位:
#Unit.py
from scipy import constants as C
print("C.mile =",C.mile) #一英里等于多少米
print("C.gram =",C.gram) #一克等于多少千克
print("C.pound =",C.pound) #一磅等于多少千克
print("C.gallon =",C.gallon) #一加仑等于多少立方米
执行结果
C.mile = 1609.3439999999998
C.gram = 0.001
C.pound = 0.45359236999999997
C.gallon = 0.0037854117839999997
21.2 特殊函数
special模块包括了数量众多的基本及特殊数学函数。下述程序可以打印这些函数的列表:
#Special.py
from scipy import special as S
import pprint
pprint.pprint([x for x in dir(S) if not x.startswith("_")])
我们简要地介绍两个函数。Gamma函数Γ在统计学中有重要应用,其定义为:
Γ ( z ) = ∫ 0 ∞ t z − 1 e − t d t Γ(z)=\int_0^{\infty}{t^{z-1}e^{-t}dt} Γ(z)=∫0∞tz−1e−tdt
special模块的gamma()函数可计算上述函数的值。
#Gamma.py
import scipy.special as S
print("gamma(5)=",S.gamma(5))
print("gamma(1+1.2j)=",S.gamma(1+2.1j)) #复数参数
执行结果
gamma(5)= 24.0
gamma(1+1.2j)= (0.13138722151786375+0.02710705024601709j)
受限于计算机内部浮点数的表达形式,计算机无法表达非常接近于1的实数,但可以表达非常接近于0的实数。比如,下述的v1的期望值是1.0 + 1e-25,但实际打印出来,其值为1.0。使用math.log(v1)求对数,就是对1.0求对数,结果为0.0。
#Log1p.py
import math
import scipy.special as S
v1 = 1.0 + 1e-25
print("v1=",v1, " #1.0 + 1e-25")
print("math.log(v1)=",math.log(v1))
v2 = 1e-25
print("v2=",v2)
print("S.log1p(v2)=",S.log1p(v2))
执行结果
v1= 1.0 #1.0 + 1e-25
math.log(v1)= 0.0
v2= 1e-25
S.log1p(v2)= 1e-25
special模块中的log1p()函数解决了这个问题,log1p(x)形式上等价于log(1+x),但其内部小心地避免了用浮点数来表达1 + x。从上述程序的执行结果看,log1p(v2)非常好地计算了1+v2,也就是1+1e-25的对数值。
21.3 优化-optimize
optimize模块提供了许多数值优化算法,提供非线性方程组求解、最小二乘法拟合、计算函数局域或者全域最小值等功能。在这里,我们介绍一下最小二乘拟合算法。
假设已知变量y和变量x之间存在函数关系y = f(x)。通过实验,我们观察到一些离散的实验数据(xi, yi),然后,通过这些实验数据,来确定上述函数关系中的参数。比如,如果y与x之间满足形如y = kx+b的函数形式,那么,最小二乘法拟合就是要找到最佳的参数集p = {k,b},使得下述函数S的值为最小:
S ( p ) = ∑ i = 1 m [ y i − f ( x i , p ) ] 2 S(p)=\sum_{i=1}^{m}[y_i-f(x_i,p)]^2 S(p)=i=1∑m[yi−f(xi,p)]2
粗浅地说,就是要找到最佳的k和b,使得通过函数关系计算出来的y值与实验数据尽可能一致。
微实践 - 最小二乘估计客观视力
眼科医学实践中,有时会有患者出于特殊目的不愿意配合普通的视力表检查,试图假装“眼盲”来获取不恰当的经济利益,这在工作伤害和人身伤害纠纷中很常见。一种称为视觉诱发电位的检查技术可以鉴别受检者的诈盲。当向受检者呈现特定空间频率的刺激图形时,受检者的视觉皮层会因为分辨出刺激图形而产生脑电信号,这种脑电信号的产生不以受检者的主观意志为转移。通过安置于头部特殊位置的皮肤电极,可以采集受检者接受不同空间频率刺激时的脑电信号,用来以帮助评价受检者真实的客观视力。眼科学大夫们相信,受检者的视觉诱发电位信号的振幅与其可鉴别的刺激图形空间频率间存在着函数关系。本例中,我们假设该函数形为 y = kx + b。
现在有一位受检者,我们测得了下述实验数据,其中,cpd为空间频率,这个值越高,说明刺激图形越精细(对应标准对数视力表更下方的E形符号)。
| 空间频率/cpd | 信号振幅/μV | 空间频率/cpd | 信号振幅/μV |
|---|---|---|---|
| 4.02 | 8.11 | 6.04 | 10.43 |
| 8.05 | 6.72 | 10.06 | 6.09 |
| 12.07 | 4.3 | 13.48 | 5.04 |
| 15.09 | 3.23 | 17.3 | 1.66 |
| 20.12 | 1.03 | 24.14 | 1.58 |
接下来,我们应用这些数据来进行最小二乘拟合。
#Leastsq.py
import numpy as np
from scipy import optimize
from matplotlib import pyplot as plt
x = np.array([4.02,6.04,8.05,10.06,12.07,13.48,15.09,17.3,20.12,24.14])
y = np.array([8.11,10.43,6.72,6.09,4.3,5.04,3.23,1.66,1.03,1.58])
def residuals(p):
"计算以p=(k,b)为参数的直线与实验数据之间的误差"
k,b = p
print("try k=",k,"b=",b)
return y - (k*x+b)
#leastsq()使得residuals()函数的输出数组的平方和为最小,[1,0]为初值
r = optimize.leastsq(residuals,[1,0])
k,b = r[0]
print("k=",k,"b=",b)
#计算y=0时的x值
print("x value when y=0:",-b/k)
执行结果
try k= 1 b= 0
try k= 1.0 b= 0.0
try k= 1.0 b= 0.0
try k= 1.0000000149011612 b= 0.0
try k= 1.0 b= 1.4901161193880158e-08
try k= -0.44638664967780084 b= 10.63854270941558
try k= -0.4463866430261214 b= 10.63854270941558
try k= -0.44638664967780084 b= 10.638542867942219
try k= -0.446386640389808 b= 10.638542630761927
k= -0.446386640389808 b= 10.638542630761927
x value when y=0: 23.832573979973503
上述代码中,residuals§中的参数p为当前k值和b值构成的元组(k,b)。该函数根据x数组以及k,b参数计算理论y数组 - k*x+b, 然后用实验y数组减去理论y数组,得到误差数组。显然,返回的误差数组是一个长度为10的一维数组(x,y的长度均为10)。
leastsq(residuals,[1,0])以k=1, b=0为初始值,然后按照一定的数学规则去尝试不同的k,b值,直到residuals()返回的误差数组的平方和为最小。上述程序的输出结果中,我们可以看到leastsq()函数尝试过的不同的k,b值。
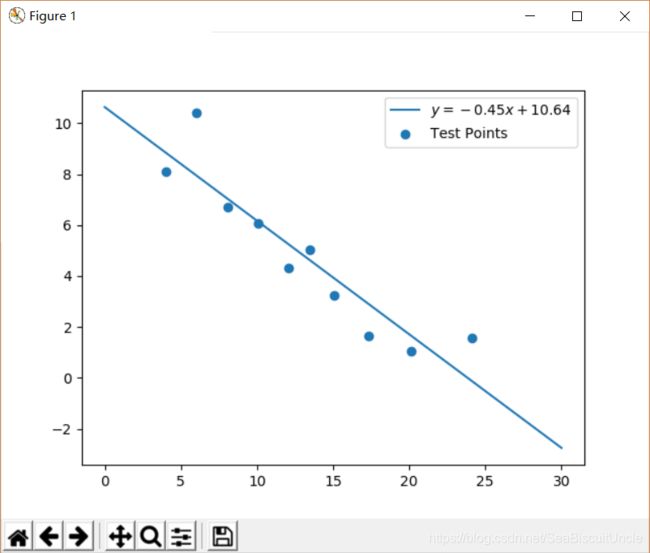
计算出k,b值后,y与x的函数关系也就确定:y = -0.45x + 10.64。在本例中,正常的人视力极限就是那个导致视觉诱发电位的振幅信号消失(=0)的最大空间频率。现在令y=0,则x = -b/k = 23.83。也就是说,当刺激图形的频率增加到23.83cpd时,受检者的视觉皮层不能产生有效的视觉诱发电位信号,这个空间频率就是受检者的视力极限。根据换算,该受检者的视力为20/25(Snellen视力表示法),换算成国内常用的对数视力就是0.8。请读者忽略眼视光学中空间频率至视力的换算关系。
我们使用下述代码绘制了实验数据的散点图以及拟合后的曲线:
#Leastsq.py
...
plt.scatter(x,y,label="Test Points") #画散点图
X = np.linspace(0,30,100) #画直线图
Y = k*X + b
sLabel = "$y={:.2f}x+{:.2f}$".format(k,b)
plt.plot(X,Y,label=sLabel)
plt.legend() #显示图示
plt.show()
plt.scatter()用于绘制散点图, 共有10个点,每个点的横坐标来自实验x数组,纵坐标则来自实验y数组。label参数用于指定图示。接下来,我们生成了值域为0-30共100个数的等差数列X,再使用k,b参数计算出拟合直线的Y数组,最后用plt.plot(X,Y,label=sLabel)绘制拟合直线的折线图。注意,此处的sLabel以"$"符号开头和结束,这是LaTeX语法,专门用于生成数学公式。plt.legend()负责将右上角的图示显示出来。
21.4 线性代数-linalg
numpy和scipy都有线性代数模块linalg,scipy的linalg更全面。借助于linalg模块,可以轻松解决解线性方程组、求最小二乘解、求特征值和特征向量、奇异值分解等线性代数问题。这里,我们讨论最简单的解线性方程组。
常规意义上的线性方程组表现为Ax = b的形式,其中A为n行n列的方阵,b为长为n的向量。 解线程方程组,就是要计算x = A-1b。x也应为一个长为n的向量。当然,x,b也可视为n行1列的矩阵。
方法1:我们先求A的逆,再乘以矩阵b。
#Linalg1.py
import numpy as np
from scipy import linalg
import timeit
n = 10
A = np.random.rand(n,n) #随机数矩阵A(10,10)
b = np.random.rand(n) #随机数矩阵b,(10,)
print("shape of A:",A.shape)
print("shape of b:",b.shape)
x = np.dot(linalg.inv(A),b) #A求逆,再乘以b
print("x=",x)
print("shape of x:",x.shape) #结果矩阵x,(10,)
print("Time cost of 100 runs:",end="\t")
print(timeit.timeit("np.dot(linalg.inv(A),b)", number=100, globals=globals()))
执行结果
shape of A: (10, 10)
shape of b: (10,)
x= [-0.28212025 -1.33259652 0.84617787 -0.2331461 1.00000274 1.08582473
-0.83282803 -0.65152769 -0.34456785 1.3682035 ]
shape of x: (10,)
Time cost of 100 runs: 0.01988152700000001
这里的linalg.inv(A)对矩阵A求逆,np.dot()负责计算两个矩阵的乘积。timeit.timeit()函数将上述核心求解过程执行100次,统计总执行时间,单位为秒。其中,numer参数指定重复计算的次数,globals=globals()把当前作用域字典传递给timeit()函数,以便其内部重复执行np.dot(linalg.inv(A),b)时使用。可以看到,计算100次,总耗时0.0199秒,即19.9毫秒。
方法2:
#Linalg2.py
...
n = 10
A = np.random.rand(n,n)
b = np.random.rand(n)
...
x = linalg.solve(A,b) #唯一区别:使用linalg.solve()进行计算
...
print("Time cost of 100 runs:",end="\t")
print(timeit.timeit("linalg.solve(A,b)", number=100, globals=globals()))
执行结果
shape of A: (10, 10)
shape of b: (10,)
x= [ 2.38796492 2.47056651 -2.20444094 2.52781153 -0.63039871 -2.97342647
0.93749006 1.43893311 -1.51257363 0.02269402]
shape of x: (10,)
Time cost of 100 runs: 0.006561185000000025
方法2当中,我们没有借助于显式的矩阵求逆和矩阵乘法,而是借助于linalg.solve()方法。从timeit()的计时看,同样的数据规模,同样执次100次,费时为6.6毫秒,比方法1要快。作者这里需要说明,把n的值变大一些,比如100,再把执行次数改为10000,才能更好地排除偶然因素对执行时间的影响。
更一般地,任何C=A-1B形式的矩阵运算,都可以用linalg.solve()求解,其形式为C = linalg.solve(A,B)。
21.5 数值积分-integrate
integrate模块提供了好几种数值积分的方法,包括常微分方程组(ODE)的数值积分。相关函数列表如下:
| 函数名 | 作用 | 函数名 | 作用 |
|---|---|---|---|
| quad() | 一元定积分 | dblquad() | 二元定积分 |
| triquad() | 三元定积分 | odeint() | 计算常微分方程组的数值解 |
微实践 - 定积分求解
本小节求解下述定积分:
∫ 0.7 4 ( c o s ( 2 π x ) e − x + 1.2 ) d x \int_{0.7}^4(cos(2\pi x)e^{-x}+1.2)\mathrm{d}x ∫0.74(cos(2πx)e−x+1.2)dx
为了方便说明,我们先使用下述代码画出示意图:
#Integrate1.py
import numpy as np
from matplotlib import pyplot as plt
x = np.linspace(0,6,1000)
y = np.cos(2*np.pi*x)*np.exp(-x)+1.2
plt.axis([np.min(x),np.max(x),0,np.max(y)]) #坐标范围
plt.plot(x,y,label="$cos(2\pi x)e^{-x}+1.2$") #画曲线,带图示
plt.fill_between(x,y1=y,y2=0,where=(x>=0.7)&(x<=4), #填充积分区域
facecolor='blue',alpha=0.2)
plt.text(0.5*(0.7+4),0.4,r"$\int_{0.7}^4(cos(2\pi x)e^{-x}+1.2)\mathrm{d}x$",
horizontalalignment='center',fontsize=14) #增加说明文本
plt.legend() #显示图示
plt.show()
plt.axis()函数设定了图的坐标范围。fill_between(x,y1=y,y2=0,where=(x>=0.7)&(x<=4)…)则用于填充积分区域,其中,x和y1构成曲线1; x和y2=0构成曲线2(也就是横坐标线);该函数填充两条曲线之间x值域为[0.7,4]的部分,where参数指明了这个值域。facecolor指定填充颜色,alpha参数指定透明度。
plt.text()则在图上添加文本,前两个参数指定了文本的坐标位置,horizontalalignment='center’要求文本在指定的位置水平居中摆放(指定位置位于文本的水平中心)。r"$…$"为文本内容:字符串前加r表示放弃对字符串内的内容进行\转义;两个$包含起来说明其中的内容为LaTeX格式的公式。
显然,上述定积分就是图中阴影部分的面积。
方法1:分成小矩形,计算面积和
#Area.py
import numpy as np
x = np.linspace(0.7,4.0,1000)
y = np.cos(2*np.pi*x)*np.exp(-x)+1.2
dx = x[1] - x[0] #每个矩形的宽度
fArea = np.sum(y*dx) #矩形宽*高,再求和
print("Integral area:",fArea)
执行结果
Integral area: 4.032803310221616
上述代码中,把曲线的阴影部分分成1000个矩形,每个矩形的宽都是dx,第i个矩形的高则是yi。每个矩形的长乘宽,再求和,得积分面积。注意,上述x,y均是形状为(1000,)的数组。
方法2:使用quad()函数进行积分
#Quad.py
import math
from scipy import integrate
def func(x):
print("x=",x) #用于展示quad()函数对func的多次调用
return math.cos(2*math.pi*x)*math.exp(-x)+1.2
fArea,err = integrate.quad(func,0.7,4)
print("Integral area:",fArea)
执行结果
x= 2.35
x= 0.7430542279466668
x= 3.9569457720533334
x= 2.4613227224815875
...
x= 3.4178741117287044
Integral area: 4.029065401143393
首先,我们定义了一个函数func(),它根据x计算y值。当对单个数值进行计算时,numpy的ufunc并不具备速度优势,所以我们使用了math模块。
integrate.quad()专门用于计算一元定积分,fArea,err = integrate.quad(func,0.7,4)取x值域[0.7,4]进行数值积分,在积分过程中,会反复调用func()函数计算y值。其返回一个元组,包括积分结果及误差。
integrate.quad()计算的积分会比方法1的矩形面积求和方法更加精确。
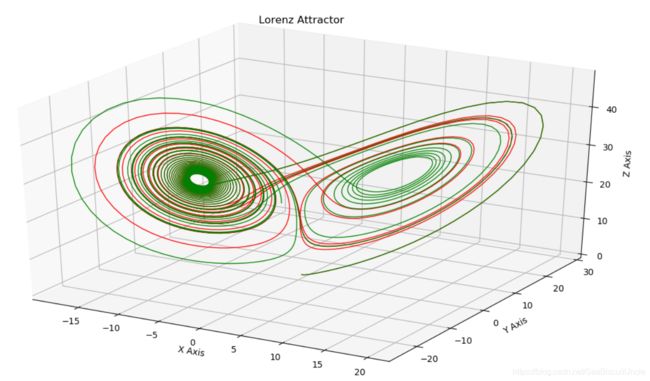
微实践 - Lorenz吸引子常微分方程组求解
在“数学之美”那一章里,为方便读者理解,Lorenz吸引子轨迹的计算采用了比较“原始”的方法。采用integrate模块中的odeint()函数可以更加方便地完成计算。Lorenz吸引子由下述三个微分方程定义:
d x d t = σ ( y − x ) , d y d t = x ( ρ − z ) − y , d z d t = x y − β z \frac{dx}{dt}=\sigma(y-x), \quad \frac{dy}{dt}=x(\rho-z)-y,\quad \frac{dz}{dt}=xy-\beta z dtdx=σ(y−x),dtdy=x(ρ−z)−y,dtdz=xy−βz
其中,σ, ρ, β为参数。这些方程定义了三维空间中的一个无质量点(x,y,z)的各轴坐标相对于时间的速度矢量。我们这里需要计算随着时间t的变化,无质量点(x,y,z)的运动轨迹,也就是一组时间点上的系统状态。
源代码如下:
#Lorenz.py
import numpy as np
from scipy import integrate
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
def lorenz(p,t,s,r,b):
x,y,z = p.tolist() #无质量点的当前位置(x,y,z)
print("x,y,z,t:",x,y,z,t) #帮助理解odeint的执行过程
return s*(y-x),x*(r-z)-y,x*y-b*z #返回dx/dt,dy/dt,dz/dt
t = np.arange(0,30,0.01)
track1 = integrate.odeint(lorenz,(0.0,1.00,0.0),t,args=(10.0,28.0,2.6))
track2 = integrate.odeint(lorenz,(0.0,1.01,0.0),t,args=(10.0,28.0,2.6))
print("type(track1):",type(track1),"track1.shape:",track1.shape)
fig = plt.figure(figsize=(12,6))
ax = fig.gca(projection='3d') #获取当前子图,指定三维模式
ax.plot(track1[:,0],track1[:,1],track1[:,2],lw=1.0,color='r') #画轨迹1
ax.plot(track2[:,0],track2[:,1],track2[:,2],lw=1.0,color='g') #画轨迹2
...
plt.show()
控制台输出:
...
x,y,z,t: -5.64346434502397 -6.711791064199058 21.875348370569984 12.728116763457338
x,y,z,t: -5.6434643216721705 -6.7117909582448 21.875348207825766 12.728116763457338
x,y,z,t: -5.776218568580239 -7.038353710472807 21.677470196579595 12.739506857199522
...
type(track1): track1.shape: (3000, 3)
首先,定义了函数lorenz(),它的任务是计算无质量点坐标各方向相对于时间t的微分值。参数s,r,b分别对应方程组中的σ, ρ, β,t为时间(在函数里没有用到),p是一个ndarray,p.tolist()将其转换成一个列表,其中包括当前无质量点的坐标。
t = np.arange(0,30,0.01)以0.01为间隔,生成从0至30(不含)的等差数列,它代表了一组离散的时间点。
integrate.odeint()则进行微分方程求解,参数lorenz指明了微分计算函数,(0.0,1.00,0.0)则为无质量点的位置初始值;t为离散时间点;args指定了要传递给lorenz函数的额外参数,对应s,r,b,为固定值。odeint()会迭代调用lorenz()函数,用于生成无质量点的运动轨迹。上述控制台输出的结果可以帮助读者理解x,y,z坐标及t的变化过程。
t是一个长度为3000的一维数组,odeint()返回结果为一个形状为(3000,3)的二维数组,用3000个离散的三维空间点来表示无质量点的运动轨迹。据信,odeint()会将lorenz()函数返回的微分值再乘以dt以获得dx,dy和dz,这个过程其实跟我们在“数学之美”那一章的模拟计算过程类似,但更高效,更精确。
track1[:,0]对track1二维数组进行下标切片,得到3000个元素的一维数组,表示3000个空间点的x坐标,y和z坐标以类似方式获得。
我们可以看到,track1-红和track2-绿仅在系统初始值上有细微差异,但随着时间的推进,其运动轨迹差异越来越大,表现出“混沌”性:南美洲一只蝴蝶扇动翅膀,会引起对面半球一场飓风。
21.6 信号处理-signal
SciPy中的signal模块支持信号处理,提供了:卷积运算、B样条、滤波等各种功能。
微实践 - ECG信号的谱分析及滤波
本节的阅读需要傅里叶级数及傅里叶变换的相关数学知识。
示范代码目录下有一个ecgsignal.dat文件,这里存储了作者采集的一段人体心电信号-ECG。这个文件以4字节浮点数存储样本,单位为μV,采样总数 = 文件大小 / 4,采样频率 = 2000样本/秒。需要说明的是,这个心电信号不是标准的医用心电信号,作者在一台其它用途的医用电生理设备上,用左手拿着正电极,右手拿着负电极,简单记录了上述信号。而且,作者故意没有涂用于皮肤电极的导电膏,以便引入“工频干扰”。
- 分析信号的频谱 - spectrum
心电信号可以视为定义在时间t上的函数,把这个函数进行傅里叶级数展开,可以将其表达成不同频率/周期的正弦函数的和。而这些正弦项的系数,则表明了该种频率的正弦项在信号构成中的重要程度。所谓的频谱分析,就是把时间t上的函数,转换成频率f上的函数,即把信号从时域转换到频域。这种转换,可以通过傅里叶变换实现。在离散的计算机世界里,对应的算法工具称为快速傅里叶变换 - Fast Fourier Transform,简称FFT。
#Spectrum.py
import numpy as np
from matplotlib import pyplot as plt
iSampleRate = 2000 #采样频率,每秒2000个样本
x = np.fromfile("ecgsignal.dat",dtype=np.float32)
iSampleCount = x.shape[0] #采样数
t = np.linspace(0,iSampleCount/iSampleRate,iSampleCount)
xFFT = np.abs(np.fft.rfft(x)/iSampleCount) #快速傅里叶变换
xFreqs = np.linspace(0, iSampleRate/2, int(iSampleCount/2)+1)
plt.figure(figsize=(10,6))
ax0 = plt.subplot(211) #画时域信号
ax0.set_xlabel("Time(s)")
ax0.set_ylabel("Amp(μV)")
ax0.plot(t,x)
ax1 = plt.subplot(212) #画频域信号-频谱
ax1.set_xlabel("Freq(Hz)")
ax1.set_ylabel("Power")
ax1.plot(xFreqs, xFFT)
plt.show()
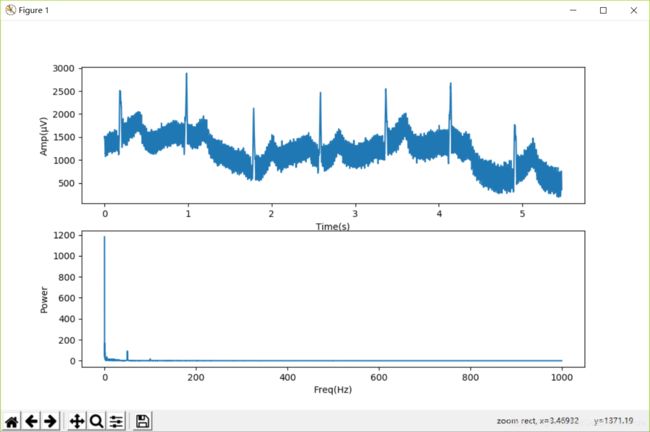
先点下方工具栏中的放大镜,然后按住鼠标左键框选放大,可以帮助我们帮察信号及频谱的细节:

np.fromfile(“ecgsignal.dat”,dtype=np.float32)从文件读取信号数据,numpy会以二进制格式打开文件,读取数据,并以4个字节为单位,逐一转换成np.float32类型,然后返回一个一维数组。该数组包含全部采样。 np.float32类型表示一个采样浮点数由32个bit,即4个字节构成。
np.linspace(0,iSampleCount/iSampleRate,iSampleCount)则生成了与信号x相同维度的一维数组t,其中的数据对应每个样本的采样时间。其中,iSampleCount为采样总数,iSampleRate为采样频率。如果采样总数=6000,则信号的总时间长度为6000/2000(采样频率)=3秒。后续代码中的ax0.plot(t,x)则以时间t为横轴,信号振幅x为纵轴,在ax0子图上画出时域信号。
np.fft模块支持快速傅里叶变换,其中的rfft()函数对实数信号进行FFT运算。根据计算公式,还需要将返回结果除以iSampleCount以便正确显示波形能量。
rfft()函数的返回值是iSampleCount/2+1个复数,分别表示从0(Hz)到iSampleRate/2(Hz)的频率能量。np.abs()对rfft()返回数组中的复数进行求模(abs)。受限于香农采样定理,采样频率为2000Hz的信号,有效的信号频率最高为1000Hz。
xFreqs = np.linspace(0, iSampleRate/2, int(iSampleCount/2)+1)则负责生成与xFFT中的能量相对应的频率。此时,(xFreqs,xFFT)可视为定义在频率域xFreqs上的“信号”,即原时域信号(t,x)的频谱。后续代码中的ax1.plot(xFreqs, xFFT)则以频率为横轴,能量为纵轴,在ax1子图上画出频谱。
顺便再次指出,plt.subplot(211)将当前图按2行1列划分,在1号位置(即上方位置)创建一张子图ax0,同理,plt.subplot(212)则在2号位置(即下方位置)创建一张子图ax1。
在下方频谱图中,我们看到在50Hz处存在一个巨大的峰,这些能量对应着那些叠加在原始信号上的有规律的周期小波,这就是所谓的工频干扰。读者可以数一数下方上图中从3.0秒至3.2秒的周期小波的周期(峰到峰)个数,应该是10个,0.2秒10个周期对应1秒种50个周期。我国的市电是220V/50Hz交流电,交变的电流流过市电导线,向空间辐射能量,这些辐射能量借助于人体,电极线等与市电导线的耦合电容,进入了信号放大器,形成“干扰”。此外,我们在100Hz处也可以看到频谱能量的峰,100Hz正好是50Hz 的倍频,也是所谓工频干扰的一部分。可以想象,如果同样的干扰发生在美国,其频率应为60Hz,因为当地的市电是110V/60Hz交流电。这里,50Hz的工频干扰我们将使用带阻滤波器,也叫陷波器滤除。
在频谱图中,我们还看到在0Hz附近也有较多能量,这些低频成分对应原始信号里缓慢变化的基线。这些低频成分也不具备诊断意义,需要滤除。我们选择使用一个带通滤波器,滤除3Hz以下的低频信号,同时滤除70Hz以上的高频信号。
- 滤波器设计
滤波是个宏大的课题,这里我们只能描述一种简便的应用方法,不描述背后的数学原理。
我们需要两个滤波器,其中一个是3-70Hz的带通滤波器,它保留信号中3-70Hz的频率成分,去除低于3Hz的低频部分以及高于70Hz的高频部分。另外一个是48-52Hz的带阻滤波器,别名50Hz陷波器,它去除信号中48-52Hz的成分。
下图展现了我们设计的带通滤波器(左)及带阻滤波器(右)的频率响应。横轴为频率,纵轴为滤波器对该频率信号的增益(gain),当增益为1.0时,说明该频率信号无障碍通过滤波器,当增益小于1.0时,说明通过滤波器时,该频率信号被衰减。可以看到,当滤波器的阶(order)越高,则滤波器性能越好(频响曲线陡峭),但计算量也会增加。
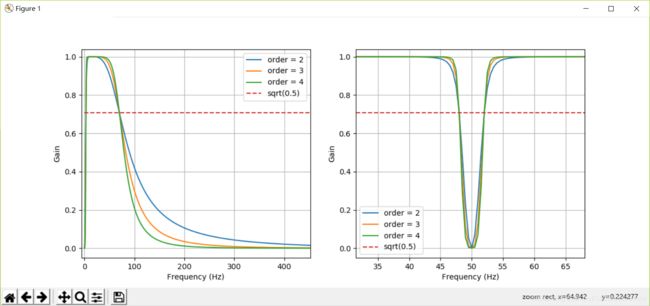
相关滤波器设计代码如下:
#FilterResponse.py
def butterBandPassFilter(lowcut, highcut, samplerate, order):
"生成巴特沃斯带通滤波器"
semiSampleRate = samplerate*0.5
low = lowcut / semiSampleRate
high = highcut / semiSampleRate
b,a = signal.butter(order,[low,high],btype='bandpass')
print("bandpass:","b.shape:",b.shape,"a.shape:",a.shape,"order=",order)
print("b=",b)
print("a=",a)
return b,a
def butterBandStopFilter(lowcut, highcut, samplerate, order):
"生成巴特沃斯带阻滤波器"
semiSampleRate = samplerate*0.5
low = lowcut / semiSampleRate
high = highcut / semiSampleRate
b,a = signal.butter(order,[low,high],btype='bandstop')
print("bandstop:","b.shape:",b.shape,"a.shape:",a.shape,"order=",order)
print("b=",b)
print("a=",a)
return b,a
iSampleRate = 2000 #采样频率
plt.figure(figsize=(12,5))
ax0 = plt.subplot(121)
for k in [2, 3, 4]:
b, a = butterBandPassFilter(3,70,samplerate=iSampleRate,order=k)
w, h = signal.freqz(b, a, worN=2000)
ax0.plot((iSampleRate*0.5/np.pi)*w,np.abs(h),label="order = %d" % k)
ax1 = plt.subplot(122)
for k in [2, 3, 4]:
b, a = butterBandStopFilter(48, 52, samplerate=iSampleRate, order=k)
w, h = signal.freqz(b, a, worN=2000)
ax1.plot((iSampleRate*0.5/np.pi)*w,np.abs(h),label="order = %d" % k)
控制台输出:
bandpass: b.shape: (5,) a.shape: (5,) order= 2
b= [ 0.00961483 0. -0.01922967 0. 0.00961483]
a= [ 1. -3.70024346 5.14358108 -3.18588885 0.74255496]
bandpass: b.shape: (7,) a.shape: (7,) order= 3
...
bandpass: b.shape: (9,) a.shape: (9,) order= 4
...
下述讨论中,f0等于采样频率的一半,即代码中的iSampleRate*0.5,或者samplerate*0.5。
从控制台输出可以看到,signal.butter()函数生成滤波器的结果为两个一维数组b和a。数组里存储一些实数,滤波器的阶(order)越大,b,a包含的实数个数越多。b,a是IIR滤波器的系数。btype参数指明了滤波器的类型,bandpass意为带通,bandstop意为带阻。[low,high]则指明了滤波器的截止频率。上述代码说明,这里的low和high应等于截止频率/f0。当采样频率为2000时,f0=2000*0.5=1000,则3Hz的截止频率对应low = 3/1000 = 0.003,70Hz的截止频率对应high = 70 / 1000 = 0.07。
freqz()函数用于计算滤波器的频率响应,返回w,h两个数组。其中,w是圆频率数组,通过w*f0/π可以计算出与其对应的频率,h是w对应频率点的响应,它是一组复数,其幅值表示滤波器的增益特性,相角表示滤波器的相位特性。参数worN表明了要计算的频率的项数,该值越大,计算越精细。
上述代码中,我们生成了阶为2,3,4的3-70Hz带通滤波器共3个,阶为2,3,4的48-52Hz带阻滤波器共3个,然后分别生成并显示了其频率响应曲线,以供读者观察。上述代码中,np.abs()函数用于求复数数组的模。
上图中,我们还画了一条sqrt(0.5)的虚线,这里对应着所谓的-3dB增益。此处,对应频率的信号的功率缩减为最高功率的一半。
可以看到,在3-70Hz带通滤波器的作用下,0Hz附近的极低频成分消失了,70Hz以后的高频成分也得到有效抑制。同时,我们注意到100Hz的干扰成分仍有残留。
在48-52Hz带阻滤波器的作用下,50Hz附近工频干扰几乎完全消失。上图中,我们看到了基线不飘移,50Hz工频周期波完全去除后的“干净”的ECG信号。这个信号来自于心脏,常在医用心电监护仪上看到。每个“尖波”对应着一次心跳,读者可以计算一下作者记录这段信号时的心率。
相关滤波的代码如下:
#Filter.py
iSampleRate = 2000 #采样频率,每秒2000个样本
x = np.fromfile("ecgsignal.dat",dtype=np.float32)
#进行带通滤波
b,a = butterBandPassFilter(3,70,iSampleRate,order=4)
x = signal.lfilter(b,a,x)
#进行带阻滤波
b,a = butterBandStopFilter(48,52,iSampleRate,order=2)
x = signal.lfilter(b,a,x)
... #谱分析及画图部分代码略
滤波的代码十分简单。signal.lfilter()将滤波器返回的b,a数组应用于信号x上,滤波后返回一个新数组。读者一定有点好奇,lfilter()内部到底做了些什么。对于FIR-有限脉冲响应滤波器,a组系数不适用,对于输出信号数组y的任意点y[i],其值为:
y i = b 0 x i + b 1 x i − 1 + . . . + b p x i − p y_i=b_0x_i+b_1x_{i-1}+...+b_px_{i-p} yi=b0xi+b1xi−1+...+bpxi−p
这就是个简单的乘积和。对于IIR-无限脉冲响应滤波器,对于输出信号数组y的任意点y[i],其值为:
y i = b 0 x i + b 1 x i − 1 + . . . + b p x i − p − a 1 y i − 1 − a 2 y i − 2 − . . . − a q y i − q a 0 y_i=\frac{b_0x_i+b_1x_{i-1}+...+b_px_{i-p}-a_1y_{i-1}-a_2y_{i-2}-...-a_qy_{i-q}}{a_0} yi=a0b0xi+b1xi−1+...+bpxi−p−a1yi−1−a2yi−2−...−aqyi−q
上述两个公式中,p+1为b数组的元素个数;q+1为a数组的元素个数。
巴特沃斯滤波器只是IIR滤波器的一种。 使用firwin()、remez()等函数可以设计FIR滤波器。iirdesign()函数则可以帮助设计IIR滤波器。要想彻底弄明白滤波器背后的数学原理,不是一件容易的事情。
21.7 插值-interpolate
插值和拟合(如最小二乘拟合)都试图通过已知的实验离散数据求未知数据。与拟合不同,插值要求曲线通过所有已知数据点。interpolate模块用于此目的。
21.7.1 一维interp1d
我们从最简单的一维插值说起。为了让读者明白什么是插值,我们生成了[0,10]上共10个元素的等差数列及其正弦值,模拟所谓的10个实验数据点。这10个实验数据点的散点图如下图中的points子图。
#Interpolate.py
from scipy import interpolate
import numpy as np
from matplotlib import pyplot as plt
x10 = np.linspace(0,10,10)
y10 = np.sin(x10)
plt.figure(figsize=(12,6))
ax = plt.subplot(231) #2行3列,在位置1创建子图
ax.scatter(x10,y10,c='black') #画散点图
ax.set_title("points")
假设在某项科学试验中,我们测试并记录了上述10个试验点。现在要从这10个试验推测y和x之间的函数关系,并以此为依据,计算其它x所对应的 y值。这个过程就是所谓的“插值”。一眼望去,这些点是散乱没有规律的,难以推断背后的函数关系。在一元函数关系中,该插值可以通过interp1d类型来完成。注意interp1d是一个类型,不是函数。interp1d()是这个类的构造函数的调用形式。
#Interpolate.py
x100 = np.linspace(0,10,100) #[0,10]的包含100个元素的等差数列
colors = ['red','green','blue','purple']
for i,kind in enumerate(['nearest','zero','slinear','quadratic']):
f = interpolate.interp1d(x10,y10,kind=kind) #从10个实验数据点插值
print("type of f:",type(f))
y100 = f(x100) #应用插值结果计算100个数的“函数”值
ax = plt.subplot(232+i) #2行3列,2+i位置建子图
ax.scatter(x10,y10)
ax.plot(x100,y100,c=colors[i]) #画100点的折线图以反应“函数”关系
ax.set_title(kind)
plt.subplots_adjust(left=0.05,right=0.95,bottom=0.05,top=0.95,
wspace=0.2,hspace=0.2) #调整子图间距等
plt.show()
控制台输出:
type of f:
...
type of f:
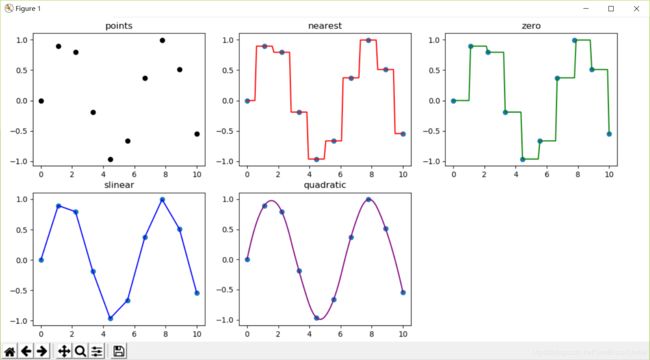
上述代码的绘图结果见上图中的nearest, zero, slinear, quadratic子图。
interpolate.interp1d类型的构造函数接受(x,y,kind)等参数。其中,x,y提供了实验数据点,kind则指明了插值类型。该构造函数返回一个对象f,这个对象f内部包括了插值后的“函数关系”。f对象是callable-可调用的,也就是说它也是一个函数。f(x100)将[0,10]的包含100个数的等差数列交给f“函数”进行计算,得y100,y100中的数值就是插值推测的结果。如果读者对f到底是对象还是函数感到疑惑,请回顾“面向对象”一章的观点:万物皆对象。
我们逐一使用四种kind进行插值计算,并把相关结果绘制出来供读者观察。可以看到,quadratic插值结果几乎跟原始sin()函数一模一样。plt.subplot(232+i)意味着将图(figure)分成2行3列,在第2+i个位置上创建一个子图 - axes。
kind参数有如下可选值:
| 插值类型 | 说明 |
|---|---|
| zero,nearest | 阶梯插值,相当于0阶B样条曲线; |
| slinear, linear | 线性插值,相当于1阶B样条曲线,简单地说,就是实验数据点的折线连接; |
| quadratic | 二阶插值,即2阶B样条曲线; |
| cubic | 三阶插值,3阶B样条曲线;事实上,kind参数可以为int,直接指定阶数。 |
需要注意的是,interp1d对象取得后,也只能计算由实验数据所框定的数值范围的函数。上例中,f([1,9])是合法的,而f([12,19])则会产生异常,因为12,19都超出了由实验数据点所框定的值域。
21.7.2 拟合与外推UnivariateSpline
interp1d的插值曲线要求经过所有实验数据点,并且,不能进行外推:即计算实验数据点范围之外的函数值。UnivariateSpline类的插值比interp1d更高级,允许外推和拟合(曲线不经过实验数据点)。
为解释UnivariateSpline类型,我们先在没有噪声的标准正弦数据点上进行插值和外推。
#UnivariateSpline.py
import numpy as np
from scipy import interpolate
from matplotlib import pyplot as plt
plt.figure(figsize=(12,4))
x = np.linspace(0,10,20) #[0,10]含20个值的等差数列
y = np.sin(x) #y = x的正弦
plt.scatter(x,y,s=20,label="points") #画散点图
xs = np.linspace(0,12,100) #[0,12]含100个值的等差数列,12>10,外推
ys = interpolate.UnivariateSpline(x,y,s=0)(xs) #由(x,y)插值,函数应用于xs
plt.plot(xs,ys,lw=2,label="spline,s=0") #画(xs,ys),ys由插值函数计算而来
plt.plot(xs,np.sin(xs),lw=2,label="sin(x)") #画标准正弦函数(xs,np.sin(xs))
plt.legend() #显示图示
plt.show()
这行代码需要进行解释:ys = interpolate.UnivariateSpline(x,y,s=0)(xs)。类似于interp1d,UnivariateSpline也是一个类型,其构造函数接受(x,y)作为实验数据点,返回一个插值对象。这个对象类型为UnivariateSpline,同时也是一个可调用对象-函数。为帮助读者理解,这行代码可以拆成两行:
f = interpolate.UnivariateSpline(x,y,s=0)
ys = f(xs)
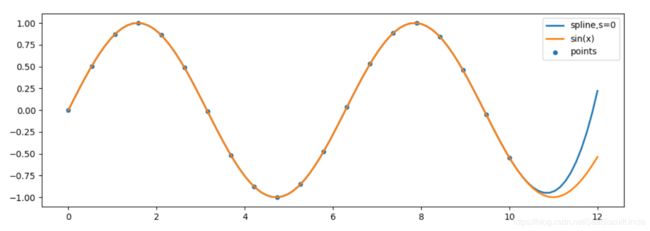
我们使用这个插值对象/函数来计算xs,返回包含部分外推的函数结果ys。请注意,试验数据点中x的值域为[0,10],而xs的值域为[0,12],超出了原有范围。
为了反应插值函数的准确性,我们还画了一条标准的正弦曲线sin(x)。可以看到,在值域[0,10]范围内,插值曲线与标准正弦几乎完全重合,但在外推的部分,即[10,12]这个区间,效果并不理想。
上述插值类构造函数的完整调用形式为:
UnivariateSpline(x, y, w=None, bbox=[None, None], k=3, s=None, ext=0, check_finite=False)
其中,w可以为每个数据指定权重;k默认为3,指定样条曲线的阶;s则是平滑系数,它使得最终生成的样条曲线满足下述条件:
s u m ( ( w [ i ] ∗ ( y [ i ] − s p l ( x [ i ] ) ) ) ∗ ∗ 2 , a x i s = 0 ) < = s sum((w[i] * (y[i]-spl(x[i])))**2, axis=0) <= s sum((w[i]∗(y[i]−spl(x[i])))∗∗2,axis=0)<=s
可以看出,当s>0时,样条曲线-spl不一定通过实验数据点,可视为曲线拟合。当s=0,样条曲线必须通过实验数据点。在本例中,s=0,我们看到所有的实验数据点都在样条曲线"spline,s=0"上。
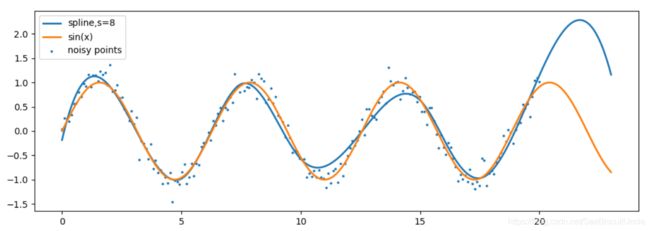
在实践当中,误差永远存在,可以认为实验数据点永远都包括噪声。接下来,我们给实验数据点加入一些噪声,再试图进行插值拟合。
#UnivariateSpline2.py
import numpy as np
from scipy import interpolate
from matplotlib import pyplot as plt
plt.figure(figsize=(12,4))
x = np.linspace(0,20,200) #[0,20]等差数列,200个值
y = np.sin(x) + np.random.standard_normal(len(x))*0.16 #带噪声正弦
plt.scatter(x,y,s=3,label="noisy points") #散点图:噪声实验数据点
xs = np.linspace(0,23,2000) #[0,23]等差数列,2000个值
ys = interpolate.UnivariateSpline(x,y,s=8)(xs) #由(x,y)插值,函数应用于xs
plt.plot(xs,ys,lw=2,label="spline,s=8") #画(xs,ys),ys由插值函数计算而来
plt.plot(xs,np.sin(xs),lw=2,label="sin(x)") #画标准正弦函数(xs,np.sin(xs))
plt.legend()
plt.show()
执行结果
np.random.standard_normal()函数生成len(x)个标准正态分布的随机数,这些随机数的取值范围为0-1,乘以0.16以控制其范围。
本次插值过程中,我们指定平滑参数s=8,这将允许样条曲线不经过实验数据点。我们看到,由于噪声的存在,即便在试验数据点的值域[0,20]范围内,插值函数未能与标准正弦曲线完全重合。在外推的值域部分,即[20,23],则差得更多。
21.7.3 二维插值
二元函数形如z = f(x,y),对其进行插值则需要使用interp2d类型。
#interp2d.py
import numpy as np
from matplotlib import pyplot as plt
from matplotlib import cm
from scipy import interpolate
plt.figure(figsize=(12,4))
y,x = np.ogrid[-2:2:20j,-2:2:20j]
z = (x+y)*np.exp(-x**2-y**2) #20x20的实验数据点
extent = [np.min(x),np.max(x),np.min(y),np.max(y)]
ax = plt.subplot(131)
ax.imshow(z,extent=extent,cmap=cm.rainbow)
ax.set_title("20x20")
func = interpolate.interp2d(x,y,z,kind='cubic') #二维插值
x1 = np.linspace(-2,2,300)
y1 = np.linspace(-2,2,300)
z1 = func(x1,y1) #根据插值函数计算函数值,要求参数为一维数组
ax = plt.subplot(132)
ax.imshow(z1,extent=extent,cmap=cm.rainbow)
ax.set_title("interp2d_300x300")
y2,x2 = np.ogrid[-2:2:300j,-2:2:300j]
z2 = (x2+y2)*np.exp(-x2**2-y2**2) #计算标准函数并显示以便对照
ax = plt.subplot(133)
ax.imshow(z2,extent=extent,cmap=cm.rainbow)
ax.set_title("original_300x300")
plt.show()
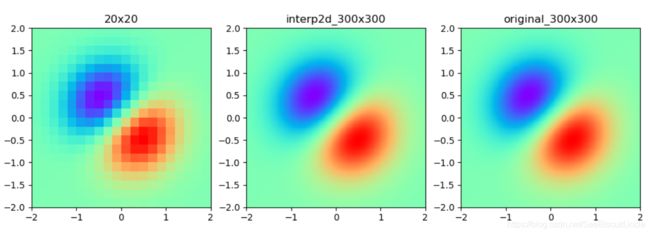
上述代码的第一部分生成了函数:
z ( x , y ) = ( x + y ) e − x 2 − y 2 z(x,y)=(x+y)e^{-x^2-y^2} z(x,y)=(x+y)e−x2−y2
的20x20个实验数据点,作为插值用。这20x20个数据点作为图像描绘了出来,可以看到,图像很粗糙(图左)。
上述代码的第二部分则对实验数据点使用类型interp2d(x,y,z…)进行了插值,得到可执行对象func。然后使用可执行对象func对300x300个(x,y)点计算z值,并描绘成图像(图中)。需要注意的是,二维插值对象要求参数必须是一维数组,其内部计算时,会对输入参数进行类似“广播”的处理。
上述代码的第三部分则计算并描绘了标准的函数图像(图右)。可以看到,插值生成的函数图像与标准的函数图像高度相似。
此外,通过splev, splprep等类型能进行参数曲线的插值。这些参数曲线可以是二维甚至高维空间的曲线。通过pchip类型则可以进行所谓单调插值。
21.8 稀疏矩阵、图像处理、统计及其它
本小节简介一下其它无法详细介绍的重要模块。
数学中的矩阵通常用计算机里的多维数组来表示。但如果矩阵很稀疏:即矩形的大多数元素都是0,用ndarray进行存储就非常地浪费。scipy.sparse模块提供了多种表示稀疏矩阵的格式;scipy.sparse.linalg则提供了对稀疏矩阵进行线性代数运算的专用函数;scipy.sparse.csgraph则可以对稀疏矩阵所代表的“图”进行搜索,比如应用著名的Dijkstra算法进行单源最短路径求解。
scipy.ndimage提供了基础的图像处理功能, 包括:
| 模块 | 用途 | 模块 | 用途 |
|---|---|---|---|
| filters | 图像滤波 | fourier | 傅里叶变换 |
| interpolation | 图像插值、旋转、仿射变换 | measurements | 图像测量 |
| morphology | 形状学处理 |
事实上,有比scipy更加强大的图像处理库,比如opencv-python, pillow, scikit-image等。
stats模块提供数理统计计算支持。包括连续、离散概率分布、卡方分布及其检验、t分布及其检验、二项和泊松分布等功能。
spatial模块则提供众多的空间算法,包括凸包、K-d树、沃德罗伊图、德劳内三角化等。
21.9 小结
我们真的浅尝则止了,scipy库十分强大。提醒读者,任何时候,当你试图进行一些跟"科学"有关的计算,别忘记先查询一下scipy是否提供相应支持,以避免重新发明轮子。与SciPy不同,Python社区里还有一个叫做SymPy的符号运算库,用它可以进行数学表达式的符号推导和演算。
本文节选自作者的《Python编程基础及应用》视频教程。想完整零基础学习Python程序设计,欢迎使用此免费视频教程。