5 7 级 错 位 打 击 赛
本篇博客并不会讲任何算法,所以极水
博主写这篇博客完全是出于在机房颓废没有事情做,顺便整理一下模拟考试的题目,所以不会像之前那样完善
T1
传送门:https://www.luogu.com.cn/problem/U121235?contestId=31441
显然,这是一个数据结构题(线段树),但是由于考试的时候没有推出标记下传的方法来,所以写了一个暴力,拿了40分的部分分
因为本人写的代码实在太糟糕了(其实是懒得写,反正有学长的详细思路解释,我就直接\(copy\)啦),所以以下是学长的T1题解
线段树板子题没人 \(AC\) 嘛?
前言
出题人本来打算给你们 \(40pts\) 的暴力分,结果没想到数据出水了,你们暴力竟然能拿 \(70pts\),给了你们一个 \(T1\) 很好做的样子。
本着信心赛的原则,我还是很希望你们能多拿一点分数,给教练一个肯定的回答,让大家的分数好看点。
还是很希望你们能认真地听完 \(30pts\) 的正解分。
当然现在我加强了数据,暴力只能拿 \(40pts\) 了吧。
\(10pts\)
对于 \(10\)% 的数据,\(x=0\) 。
操作 \(1\) 再怎么花里胡哨都是没用的,我们只需要考虑操作 \(2\) 即可。
区间求和问题,可以直接用前缀和来做,时间复杂度 \(Θ(n)\) 。
期望得分 \(:10pts\) 。
\(20pts\)
对于另外 \(10\)% 的数据,\(1<=l=r<=n\) 。
只是多了一个单点修改的操作,只需注意我们在修改的时候是 \(-x\),可以用线段树或树状数组来做,时间复杂度 \(Θ(nlog_n)\) 。
期望得分 \(:20pts\) 。
\(40pts\)
对于另外 \(20\)% 的数据,\(1<=n,m<=5000\),\(-100<=a_i,x<=100\)。
考虑到 \(n\) 和 \(m\) 的范围很小,我们直接用最朴素的算法 "暴力" 直接做即可,时间复杂度 \(Θ(nm)\) 。
\(100pts\)
对于 \(100\)%的数据,保证 \(1<=n,m<=3*10^5\),\(-1000<=a_i,x<=1000\),\(1<=l,r<=n\) 。
看到这个数据范围,正解肯定是 \(Θ(nlog_n)\) 的数据结构无疑了 。
由于出题人没有什么好的做法,那么这道题我们还是用线段树做吧。
思考一下这道题和你们做的线段树板子有什么不同,很显然它的操作 \(1\) 变得更加毒瘤且恶心。
但是换汤不换药,线段树板子的套路在这道题上还是可以应用的,那就是:懒标记
回顾一下区间加、区间求和的懒标记:
if(x<=l&&r<=y)
{
lazy[node]+=v;
sum[node]+=(r-l+1)*v;
return ;
}
比着葫芦画瓢,我们做这道题的时候也设置一个懒标记:
\(lazy1[node]=k\) 表示线段树中 \(node\) 节点所代表的区间进行了一次操作 \(1\),要时刻注意操作 \(1\) 是以 \(-\) 开始的。
然后我们思考一下怎么 \(Θ(1)\) 地对 \(sum[node]\) 进行维护:
找规律:我们可以将第 \(k\) 个和第 \(k+1\) 个看成一组,它们的贡献之和为 \(x\) ,那么所有组的贡献总和为:\(x*\) 组数 :
但是可能还会存在一个落单的,别忘了计算这个落单的贡献。
对于 \(lazy1[node]\) 的维护,我们直接令 \(lazy1[node]+=k\) 即可 。
这样就可以了嘛?真 · 线段树板子?上述做法有什么问题嘛?
\(Problem1:\) 正负号问题 。
一个很重要的问题:我们上面的操作都是基于第一个数是 \(-\) 才行,也就是说,我们的操作形式要和题目中给出的操作 \(1\) 的形式一直才对 。
题目中的操作 \(1\) 不是以 \(-\) 的形式开始的嘛?为什么当前区间第一个数可能会是 \(+\) 的形式?
如上图所示:如果你要对 \([1,5]\) 进行操作 \(1\) ,当你递归到你的右儿子 \([4,5]\) 的时候发现是以 \(+\) 开头的,但是由于左儿子的最左端就是它父亲的最左端,所以左儿子开头的正负性和父亲开头的正负性是相等的,我们比较好判断,我们重点要判断右儿子的开头的正负性 。
想一想哈,如果左儿子的区间长度为 \(2k\),那么右儿子开头的正负性和父亲的相同;如果左儿子的区间长度为 \(2k+1\),那么右儿子开头的正负性和父亲的相反 。
\(Problem2:\) 标记下传问题
注意一下我们 \(lazy1[node]=k\) 的定义:表示线段树中 \(node\) 节点所代表的区间进行了一次操作 \(1\)。
注意到操作 \(1\) 是有两个性质的:
①. 正负号交替;②. 每一项的绝对值之差为首项的绝对值。
注意到上图右儿子中,操作 \(1\) 的首项为 \(+4x\) ,而每一项的绝对值之差为 \(x\),不符合操作 \(1\) 的定义了,所以我们不能直接维护懒标记。
提取公因式:我们将 \(+4x\) 看作是 \(+3x+x\),将 \(-5x\) 看作是 \(-3x-2x\),注意到右边的 \(+x\) 和 \(-2x\) 了没,这不就是操作 \(1\) 嘛?对于左边的 \(+3x\) 和 \(-3x\) 呢,我们可以看出一种新的操作:
\(3.l,r,y\) 表示将 \([l,r]\) 的第 \(l\) 个数减 \(y\),第 \(l+1\) 个数加 \(y\),第 \(l+2\) 个数减 \(y\) ......
即:令 \(a_l=a_l-y\),\(a_{l+1}=a_{l+1}+y\),\(a_{l+2}=a_{l+2}-y\) ...... \(a_r=a_r+(-1)^{r-l+1}y\) 。
所以对于上面的右儿子,我们可以看作是先进行了一次 \(x=-x\) 的操作 \(1\) ,再加上一次 \(y=-y\) 的操作 \(3\) 。
对于操作 \(3\),我们同样开一个懒标记 \(lazy2[node]=k\) 来进行维护,有 \(1\) 必有 \(2\) 嘛\(qwq\) 。
\(insert\)
void insert(int node,int l,int r,int x,int y,int k)
{
if(x<=l&&r<=y) //[l,r]被完全覆盖
{
int len=r-l+1; //当前区间的长度
int d=l-x; //x~l-1之间有多少个数
if(d&1) //如果l前面有有奇数个数,说明第l个数在[x,y]内是第偶数个数,那么应该是从加号开始
{
lazy1[node]-=k; //由于我们lazy1的设定是从减号开始的,所以这里应该是-=
lazy2[node]-=k*d;
//将操作1进行拆解,所提取出来的公因数的绝对值为k*d,同样我们操作3的设定也是从减号开始,所以这里还是-=
sum[node]-=(len/2)*k; //对sum[node]进行维护,将它们两两看成一组,一共有len/2组,每一组的贡献为-k
if(len&1) sum[node]+=k*(r-x+1);
//如果区间长度为奇数,说明两两一组有余,由于我们已经判断出该区间是从加号开始的,所以这个余出的数一定是加
}
else //从减开始,与上面的同理,只是符号都改成相反的而已
{
lazy1[node]+=k;
lazy2[node]+=k*d;
sum[node]+=(len/2)*k;
if(len&1) sum[node]-=k*(r-x+1);
}
return ;
}
pushdown(node,l,r); //记得标记下传
int mid=(l+r)>>1;
if(x<=mid) insert(node<<1,l,mid,x,y,k);
if(y>mid) insert(node<<1|1,mid+1,r,x,y,k);
update(node); //维护父亲节点的sum
}
\(pushdown\)
如果你已经理解了 \(insert\) 的思路,那么 \(pushdown\) 的思路也就不难了。
void pushdown(int node,int l,int r)
{
int mid=(l+r)>>1;
int len=r-l+1;
int len1=mid-l+1;
int len2=r-mid;
if(lazy1[node]) //时刻牢记lazy1是从减开始的
{
sum[node<<1]+=(len1/2)*lazy1[node]; //两两分组算贡献
if(len1&1) sum[node<<1]-=len1*lazy1[node]; //两两分组有余,那么余的这个数肯定是减的
lazy1[node<<1]+=lazy1[node]; //维护左儿子的lazy1
if(len1&1) //如果左儿子的区间长度为奇数,说明右儿子的左端点是第偶数个数,则是从加开始
{
lazy1[node<<1|1]-=lazy1[node]; //由于是从加开始,所以这里是减
lazy2[node<<1|1]-=lazy1[node]*len1;
//只有右儿子不满足操作1的性质②,因此我们要拆分操作,所以我们只维护右儿子的lazy2
sum[node<<1|1]-=(len2/2)*lazy1[node]; //两两分组算贡献
if(len2&1) sum[node<<1|1]+=lazy1[node]*len; //两两分组有余,由于右儿子是从加开始的,所以余的这个数肯定是加的
}
else //右儿子的左端点从减开始,除了符号和上面都一样
{
lazy1[node<<1|1]+=lazy1[node];
lazy2[node<<1|1]+=lazy1[node]*len1;
sum[node<<1|1]+=(len2/2)*lazy1[node];
if(len2&1) sum[node<<1|1]-=lazy1[node]*len;
}
lazy1[node]=0; //别忘了清空标记1
}
if(lazy2[node]) //下传标记2
{
if(len1&1) sum[node<<1]-=lazy2[node]; //对于操作3,发现两两算贡献的时候可以抵消,所以如果有余肯定是减的
lazy2[node<<1]+=lazy2[node]; //维护左儿子的lazy2
if(len1&1) //右儿子的左端点从加开始
{
lazy2[node<<1|1]-=lazy2[node]; //维护右儿子的lazy2,由于右儿子的左端点是从加开始的,所以这里是减
if(len2&1) sum[node<<1|1]+=lazy2[node];
}
else //右儿子的左端点从减开始,仍然只有符号不同
{
lazy2[node<<1|1]+=lazy2[node];
if(len2&1) sum[node<<1|1]-=lazy2[node];
}
lazy2[node]=0; //清空lazy2
}
}
完整版\(Code:\)
#include
#include
using namespace std;
int read()
{
char ch=getchar();
int a=0,x=1;
while(ch<'0'||ch>'9')
{
if(ch=='-') x=-x;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
a=(a<<1)+(a<<3)+(ch-'0');
ch=getchar();
}
return a*x;
}
const int N=1e5+5;
int n,m;
int a[N],sum[N<<2],lazy1[N<<2],lazy2[N<<2];
void update(int node)
{
sum[node]=sum[node<<1]+sum[node<<1|1];
}
void pushdown(int node,int l,int r)
{
int mid=(l+r)>>1;
int len=r-l+1;
int len1=mid-l+1;
int len2=r-mid;
if(lazy1[node]) //时刻牢记lazy1是从减开始的
{
sum[node<<1]+=(len1/2)*lazy1[node]; //两两分组算贡献
if(len1&1) sum[node<<1]-=len1*lazy1[node]; //两两分组有余,那么余的这个数肯定是减的
lazy1[node<<1]+=lazy1[node]; //维护左儿子的lazy1
if(len1&1) //如果左儿子的区间长度为奇数,说明右儿子的左端点是第偶数个数,则是从加开始
{
lazy1[node<<1|1]-=lazy1[node]; //由于是从加开始,所以这里是减
lazy2[node<<1|1]-=lazy1[node]*len1;
//只有右儿子不满足操作1的性质②,因此我们要拆分操作,所以我们只维护右儿子的lazy2
sum[node<<1|1]-=(len2/2)*lazy1[node]; //两两分组算贡献
if(len2&1) sum[node<<1|1]+=lazy1[node]*len; //两两分组有余,由于右儿子是从加开始的,所以余的这个数肯定是加的
}
else //右儿子的左端点从减开始,除了符号和上面都一样
{
lazy1[node<<1|1]+=lazy1[node];
lazy2[node<<1|1]+=lazy1[node]*len1;
sum[node<<1|1]+=(len2/2)*lazy1[node];
if(len2&1) sum[node<<1|1]-=lazy1[node]*len;
}
lazy1[node]=0; //别忘了清空标记1
}
if(lazy2[node]) //下传标记2
{
if(len1&1) sum[node<<1]-=lazy2[node]; //对于操作3,发现两两算贡献的时候可以抵消,所以如果有余肯定是减的
lazy2[node<<1]+=lazy2[node]; //维护左儿子的lazy2
if(len1&1) //右儿子的左端点从加开始
{
lazy2[node<<1|1]-=lazy2[node]; //维护右儿子的lazy2,由于右儿子的左端点是从加开始的,所以这里是减
if(len2&1) sum[node<<1|1]+=lazy2[node];
}
else //右儿子的左端点从减开始,仍然只有符号不同
{
lazy2[node<<1|1]+=lazy2[node];
if(len2&1) sum[node<<1|1]-=lazy2[node];
}
lazy2[node]=0; //清空lazy2
}
}
void build(int node,int l,int r)
{
if(l==r)
{
sum[node]=a[l];
return ;
}
int mid=(l+r)>>1;
build(node<<1,l,mid);
build(node<<1|1,mid+1,r);
update(node);
}
void insert(int node,int l,int r,int x,int y,int k)
{
if(x<=l&&r<=y) //[l,r]被完全覆盖
{
int len=r-l+1; //当前区间的长度
int d=l-x; //x~l-1之间有多少个数
if(d&1) //如果l前面有有奇数个数,说明第l个数在[x,y]内是第偶数个数,那么应该是从加号开始
{
lazy1[node]-=k; //由于我们lazy1的设定是从减号开始的,所以这里应该是-=
lazy2[node]-=k*d;
//将操作1进行拆解,所提取出来的公因数的绝对值为k*d,同样我们操作3的设定也是从减号开始,所以这里还是-=
sum[node]-=(len/2)*k; //对sum[node]进行维护,将它们两两看成一组,一共有len/2组,每一组的贡献为-k
if(len&1) sum[node]+=k*(r-x+1);
//如果区间长度为奇数,说明两两一组有余,由于我们已经判断出该区间是从加号开始的,所以这个余出的数一定是加
}
else //从减开始,与上面的同理,只是符号都改成相反的而已
{
lazy1[node]+=k;
lazy2[node]+=k*d;
sum[node]+=(len/2)*k;
if(len&1) sum[node]-=k*(r-x+1);
}
return ;
}
pushdown(node,l,r); //记得标记下传
int mid=(l+r)>>1;
if(x<=mid) insert(node<<1,l,mid,x,y,k);
if(y>mid) insert(node<<1|1,mid+1,r,x,y,k);
update(node); //维护父亲节点的sum
}
int query(int node,int l,int r,int x,int y)
{
if(x<=l&&r<=y) return sum[node];
pushdown(node,l,r);
int mid=(l+r)>>1;
int cnt=0;
if(x<=mid) cnt+=query(node<<1,l,mid,x,y);
if(y>mid) cnt+=query(node<<1|1,mid+1,r,x,y);
return cnt;
}
int main()
{
//freopen("country.in","r",stdin);
//freopen("country.out","w",stdout);
n=read();m=read();
for(int i=1;i<=n;i++)
a[i]=read();
build(1,1,n);
for(int i=1;i<=m;i++)
{
int opt,l,r,x;
opt=read();
l=read();r=read();
if(l>r) swap(l,r);
if(opt==1)
{
x=read();
insert(1,1,n,l,r,x);
}
else printf("%d\n",query(1,1,n,l,r));
}
return 0;
}
\(The\) \(last\)
线段树是一种很优秀的数据结构,希望你们能多加练习,体会它的魅力。
本着出于让你们练一练线段树的目的,我才出的这道题,没想到正解还真的不好做。出题人埋头苦思想了 \(2.5h\) 才想出正解,当然可能有更优的方法等待着你们来挖掘。
最后膜一下你们这群 \(Θ(n^2)\) 过 \(1e4\) 数据的卡常带师。
——暗ざ之殇
T2
讲道理,凭良心说话,T2要比T1简单亿点
传送门:https://www.luogu.com.cn/problem/U121369?contestId=31441
\(30pts\)
**首先感谢学长不杀之恩,看到数据范围,了解到一个\(30pts\)的做法,因为\(n=1\),所以输出\(0\)即可
\(100pts\)
题目描述的已经很清楚了,把问题抽象化出来,就是求节点\(1\)的单源最短路,再求所有节点到节点\(1\)的单源最短路,累加答案即可
首先,我们看到,求所有到\(1\),求\(1\)到所有第一个想到的解法应该是\(floyd\)吧
这个算法可以在\(O(n^3)\)的时间内求出全源最短路,然后我们调用我们需要的数据,累加答案即可
但是显然这不是正解,因为:
对于\(100\)%的数据,有\(n<=1000\)
\(1000^3\)你玩呢?所以我又想出了如下方案:
1、跑\(n\)遍堆优化的\(dijkstra\),然鹅,复杂度\(O(n*(m+n)logn)\),并没有什么实质上的优化
2、\(n\)遍\(spfa\),最坏复杂度\(O(n^2*m)\),依然是我们无法接受的量级
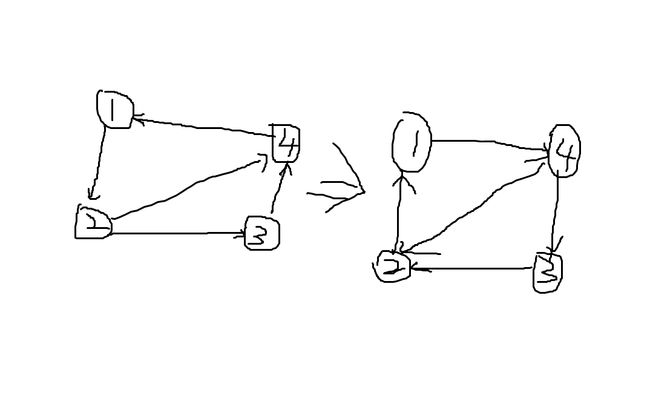
暂时没有思路,所以我在小本子上把样例画了出来,发现了这样一个有趣的现象:
(原谅我是灵魂画手)
我们发现,如上图(假设边权都是\(1\)),我们跑一遍\(1\)->\(4\)的最短路,是\(1\)->\(3\)->\(4\),如果我们把边反着建,再跑一边最短路,就是\(1\)->\(4\),也就是正向图\(4\)->\(1\)的最短路
所以我直接乱搞一波反向建边+两遍\(dijkstra\)(反正是乐多赛制可以实时观测评测结果)
直接交上去发现,真就切掉了。。。
\(AC\) \(Code\)(后来我发现洛谷上还有一个几乎一模一样的题P1629,传送门:https://www.luogu.com.cn/problem/P1629
#include
#include
#include
#include
#include
#define N 1010
using namespace std;
typedef long long int ll;
priority_queue< pair >q;
ll mapp[N][N],dis[N],vis[N],cop[N],n,m,d,ans;
void upside_down(){
for(int i=1;i<=n;i++)
for(int j=i+1;j<=n;j++)
swap(mapp[i][j],mapp[j][i]);//这里是反向建边(我比较懒直接用的邻接矩阵
}
void dijkstra(){
memset(dis,0x3f,sizeof(dis));
memset(vis,0,sizeof(vis));
dis[1]=0;
q.push(make_pair(0,1));
while(q.size()!=0){
int x=q.top().second;
q.pop();
vis[x]=1;
for(int y=1;y<=n;y++){
int z=mapp[x][y];
if(dis[y]>dis[x]+z&&vis[y]!=1){
dis[y]=dis[x]+z;
q.push(make_pair(-dis[y],y));
}
}
}
}
int main(){
scanf("%lld%lld%lld",&n,&m,&d);
memset(mapp,0x7f,sizeof(mapp));
for(ll i=0;i T3
传送门:https://www.luogu.com.cn/problem/U121284?contestId=31441
又双叒叕是一个图论题!
\(50pts\)
仍然先感谢学长不杀之恩:对于\(50\)%的数据,\(n\)<=100,所以我如果没猜错的话,这\(50pts\)应该是给了暴搜吧……但是好像机房里没有人愿意拿这个部分分唉?
\(100pts\)
扫一眼题面,我们了解到,本题要求出从\(s\)->\(e\)的一条路径,使得这条路径上,最大的边权最小,并输出这个最大边权最小值
想了一通有没有这么一个算法来应对这种问题,,,但是显然没有
突然想到,本题的答案似乎具有单调性,可以使用二分法求解
具体怎么个单调性?
首先,我们二分一个中点\(Mid\),然后在图上跑一遍,如果遇到权值比\(Mid\)值要大的边,就自动忽视掉
然后,看看剩下的这些边,能不能支持我们从\(s\)->\(e\)
如果不走比\(Mid\)权值大的边,可以支持我们从\(s\)->\(e\),说明那个最大边权最小值比\(Mid\)小,反之,比\(Mid\)大
然而还有一个问题,我们怎么判断这两个点在上述二分求解的情况中是否被联通呢?
一开始我想到了\(dfs\),但是经过我多年写暴搜\(TLE\)的惨痛教训,我真的不愿意写这个搜索了。。。
于是我又想起了一个玄学做法——跑\(dijkstra\),首先赋值\(dis\)数组为\(0x7f7f7f7f\),从\(s\)跑一遍\(dijkstra\),看看\(e\)的最短路有没有被更新,如果被更新了,说明\(s\),\(e\)联通,反之,\(s\),\(e\)不连通
然后我把这两个玄学的思路结合到了代码里:
\(Code\)
#include
#include
#include
#include
#include
using namespace std;
const int N=5005;
typedef long long int ll;
struct edge{
int to,cost;
};
vectorv[N];
priority_queue< pair >q;
ll dis[N],vis[N],cop[N],n,m,s,e;
bool dijkstra(int a,int m){
memset(dis,0x7f,sizeof(dis));
memset(vis,0,sizeof(vis));
dis[a]=0;
q.push(make_pair(0,a));
while(q.size()!=0){
int x=q.top().second;
q.pop();
for(unsigned int i=0;im) continue;
if(dis[y]>dis[x]+z){
dis[y]=dis[x]+z;
q.push(make_pair(-dis[y],y));
}
}
}
if(dis[e]>2147483646) return false;
else return true;
}
int main(){
scanf("%lld%lld",&n,&m);
for(ll i=0,x,y,z;i>1;
if(dijkstra(s,Mid)==true){
r=Mid-1;
ans=min(ans,Mid);
}else l=Mid+1;
}
printf("%lld",ans);
return 0;
}
结果\(AC\)了,比赛后学长发了一下题解,正解是用\(Kruscal\)最小生成树算法做的,然后因为我不会\(Kruscal\)所以这里直接贴一波\(std\)叭!
\(std\) \(Code\)
#include
#include
#include
#include
#include
#include
#include
using namespace std;
inline int read()
{
int a=0,b=1;
char c=getchar();
while(!isdigit(c))
{
if(c=='-')
b=-1;
c=getchar();
}
while(isdigit(c))
{
a=(a<<3)+(a<<1)+(c^48);
c=getchar();
}
return a*b;
}
int num,s,t,maxn,father[5005];
struct edge
{
int from,to,dis;
}e[400005];
bool cmp(edge a,edge b)
{
return a.dis ##其实有T4,但是是一个毒瘤高精+动规,所以劳资不写啦!!!