【最通俗易懂】A*寻路算法C#实现
A*算法其实也不复杂,首先有以下几个概念:
-
开启的节点表(OpenList)
存放着所有的待检测的节点(坐标),每次都会从其中寻找出符合某个条件的节点。
-
关闭的节点表(ClosedList)
存放着所有不会被检测的节点(坐标),每次检测都会忽略它们。
首先,我们定义了两个点,分别是起点和终点。
整个算法的核心就是启发式的权值比较,分为G和H值。
一般我们将按非斜向方向移动的距离定为10,斜向为14
-
G值
标准术语:g(n)表示从初始节点到任意节点n的代价。当前节点的G值等于移动前节点的G值加上移动到当前节点的距离。如果新路径到相邻点的距离更短,G值更小,更新相邻节点的G值。因此,同一个节点的G值会因为选取的MinFNode不同而改变。
-
H值
标准术语:h(n)表示从节点n到目标点的启发式评估代价。当前节点到终点的距离。固定不变的值。计算H值,忽略障碍(可以认为没有障碍),只计算最近的距离。
-
F值
F值为G值和H值之和
上述的基本概念理清的话,下面的算法就简单了。
辅助理解图:
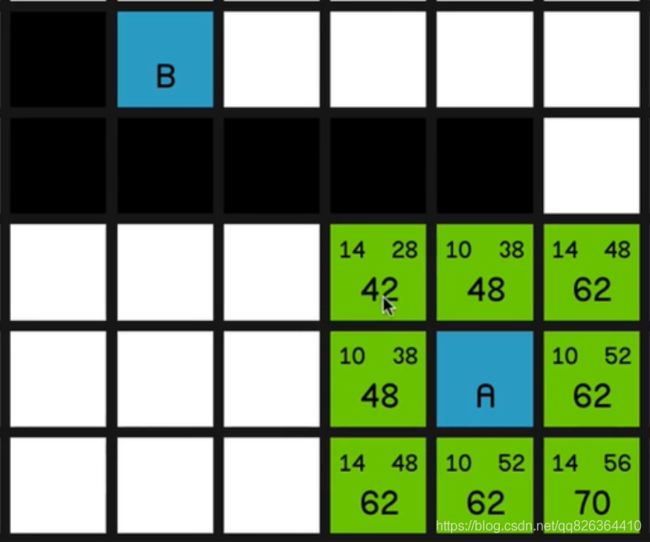
下图中A是起点,B是终点,方格中的数值,左上方表示G值,右上方表示H值,下方表示F值。
举例:鼠标指向的方格,G值为14(斜向),H值为28(当前节点距离终点B最近的距离为两个对角线的距离也就是28),所以F=G+H = 42
算法的基本逻辑基本按下述步骤走:
1.将起点放入OpenList中
2.利用While(OpenList.Count)循环, 只要OpenList.Count大于0, 就一直循环执行3, 4, 5步骤。
3.寻找开启列表中的F最小的节点MinFNode,如果F相同,选取H最小的。同时把MinFNode从OpenList移除,放入ClosedList中
4.遍历MinFNode周围的节点,忽略障碍节点和已在ClosedList中的节点,这里会有3种情况
- 相邻点不在OpenList中的,计算H值和G值(MinFNode的G值加上移动所产生的G值),并且把该相邻点的父节点设置为MinFNode (后期找到终点后,需要用父节点进行路径回溯,画出路线。),加入到开启列表OpenList中。
- 相邻点已在OpenList中的,则判断从MinFNode节点的G值加上到相邻点移动所产生的G值之和,是否小于该相邻点的G值,假设小于了,则更新该相邻点的G值为较小的那个,然后重新设置该相邻点的父节点为MinFNode
- 假设遍历到的节点是终点,则按MinFNode的父节点进行回溯,获取到起点的路径,找到最终路径
5.如果没有找到终点,回到第3步,继续执行
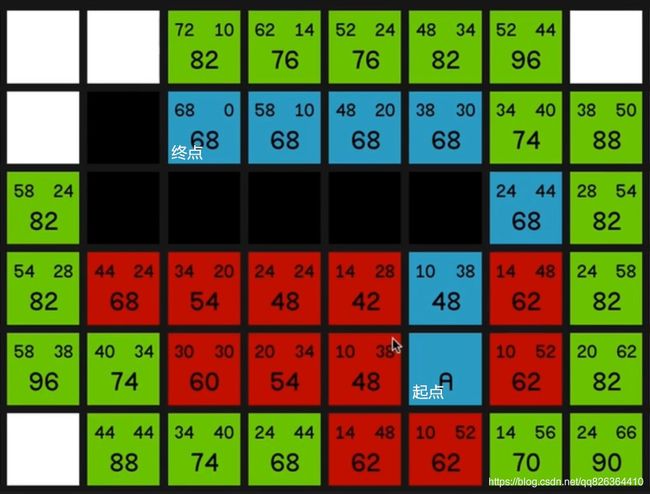
A*寻路示例:
最终的效果图:
注:下面的代码在Unity里用C#实现,整个工程我放在Github上了,获取地址超链接
Node节点实现:
using UnityEngine;
public class Node
{
//是否可以通过
public bool m_CanWalk;
//节点空间位置
public Vector3 m_WorldPos;
//节点在数组的位置
public int m_GridX;
public int m_GridY;
//开始节点到当前节点的距离估值
public int m_gCost;
//当前节点到目标节点的距离估值
public int m_hCost;
public int FCost
{
get { return m_gCost + m_hCost; }
}
//当前节点的父节点
public Node m_Parent;
public Node(bool canWalk, Vector3 position, int gridX, int gridY)
{
m_CanWalk = canWalk;
m_WorldPos = position;
m_GridX = gridX;
m_GridY = gridY;
}
}创建网格:
using System.Collections.Generic;
using UnityEngine;
public class GridBase : MonoBehaviour
{
private Node[,] m_Grid;
public Vector2 m_GridSize;
public float m_NodeRadius;
public LayerMask m_Layer;
public Stack m_Path = new Stack();
private float m_NodeDiameter;
private int m_GridCountX;
private int m_GridCountY;
void Start()
{
m_NodeDiameter = m_NodeRadius * 2;
m_GridCountX = Mathf.RoundToInt(m_GridSize.x / m_NodeDiameter);
m_GridCountY = Mathf.RoundToInt(m_GridSize.y / m_NodeDiameter);
m_Grid = new Node[m_GridCountX, m_GridCountY];
CreateGrid();
}
///
/// 创建格子
///
private void CreateGrid()
{
Vector3 startPos = transform.position;
startPos.x = startPos.x - m_GridSize.x / 2;
startPos.z = startPos.z - m_GridSize.y / 2;
for (int i = 0; i < m_GridCountX; i++)
{
for (int j = 0; j < m_GridCountY; j++)
{
Vector3 worldPos = startPos;
worldPos.x = worldPos.x + i * m_NodeDiameter + m_NodeRadius;
worldPos.z = worldPos.z + j * m_NodeDiameter + m_NodeRadius;
bool canWalk = !Physics.CheckSphere(worldPos, m_NodeRadius, m_Layer);
m_Grid[i, j] = new Node(canWalk, worldPos, i, j);
}
}
}
///
/// 通过空间位置获得对应的节点
///
///
///
/// 获得当前节点的相邻节点
///
///
/// GetNeighor(Node node)
{
List neighborList = new List();
for (int i = -1; i <= 1; i++)
{
for (int j = -1; j <= 1; j++)
{
if (i == 0 && j == 0)
{
continue;
}
int tempX = node.m_GridX + i;
int tempY = node.m_GridY + j;
if (tempX < m_GridCountX && tempX > 0 && tempY > 0 && tempY < m_GridCountY)
{
neighborList.Add(m_Grid[tempX, tempY]);
}
}
}
return neighborList;
}
private void OnDrawGizmos()
{
Gizmos.DrawWireCube(transform.position, new Vector3(m_GridSize.x, 1, m_GridSize.y));
if (m_Grid == null)
{
return;
}
foreach (var node in m_Grid)
{
Gizmos.color = node.m_CanWalk ? Color.white : Color.red;
Gizmos.DrawCube(node.m_WorldPos, Vector3.one * (m_NodeDiameter - 0.1f));
}
if (m_Path != null)
{
foreach (var node in m_Path)
{
Gizmos.color = Color.green;
Gizmos.DrawCube(node.m_WorldPos, Vector3.one * (m_NodeDiameter - 0.1f));
}
}
}
} 寻路算法的实现:
using System.Collections.Generic;
using UnityEngine;
public class FindPath : MonoBehaviour
{
public Transform m_StartNode;
public Transform m_EndNode;
private GridBase m_Grid;
private List openList = new List();
private HashSet closeSet = new HashSet();
void Start()
{
m_Grid = GetComponent();
}
void Update()
{
FindingPath(m_StartNode.position, m_EndNode.position);
}
///
/// A*算法,寻找最短路径
///
///
///
private void FindingPath(Vector3 start, Vector3 end)
{
Node startNode = m_Grid.GetFromPosition(start);
Node endNode = m_Grid.GetFromPosition(end);
openList.Clear();
closeSet.Clear();
openList.Add(startNode);
while (openList.Count > 0)
{
// 寻找开启列表中的F最小的节点,如果F相同,选取H最小的
Node currentNode = openList[0];
for (int i = 0; i < openList.Count; i++)
{
Node node = openList[i];
if (node.FCost < currentNode.FCost || node.FCost == currentNode.FCost && node.m_hCost < currentNode.m_hCost)
{
currentNode = node;
}
}
// 把当前节点从开启列表中移除,并加入到关闭列表中
openList.Remove(currentNode);
closeSet.Add(currentNode);
// 如果是目的节点,返回
if (currentNode == endNode)
{
GeneratePath(startNode, endNode);
return;
}
// 搜索当前节点的所有相邻节点
foreach (var node in m_Grid.GetNeighor(currentNode))
{
// 如果节点不可通过或者已在关闭列表中,跳出
if (!node.m_CanWalk || closeSet.Contains(node))
{
continue;
}
int gCost = currentNode.m_gCost + GetDistanceNodes(currentNode, node);
// 如果新路径到相邻点的距离更短 或者不在开启列表中
if (gCost < node.m_gCost || !openList.Contains(node))
{
// 更新相邻点的F,G,H
node.m_gCost = gCost;
node.m_hCost = GetDistanceNodes(node, endNode);
// 设置相邻点的父节点为当前节点
node.m_Parent = currentNode;
// 如果不在开启列表中,加入到开启列表中
if (!openList.Contains(node))
{
openList.Add(node);
}
}
}
}
}
///
/// 生成路径
///
///
///
private void GeneratePath(Node startNode, Node endNode)
{
Stack path = new Stack();
Node node = endNode;
while (node.m_Parent != startNode)
{
path.Push(node);
node = node.m_Parent;
}
m_Grid.m_Path = path;
}
///
/// 获得两个节点的距离
///
///
///
/// 推荐一个b站的讲解A*算法的视频:https://www.bilibili.com/video/av32847834/
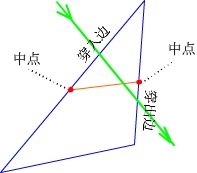
这里补充一下三角形网格如何使用A*算法,如下图,绿色直线代表最终路径和方向,路径线进入三角形的边称为穿入边,路径线出去的边称为穿出边。每个三角形的花费(g值)采用穿入边和穿出边的中点的距离(图中红线),至于估价函数(h值)使用该三角形的中心点(3个顶点的平均值)到路径终点的x和y方向的距离。