空间解析几何与向量代数
一. 向量及其线性运算
- 模长等于 1 1 1的向量称为单位向量。
- 向量的线性运算:
①加法;
②数乘: λ α ⃗ = ( λ a x , λ a y , λ a z ) \lambda\vec{\alpha}=(\lambda a_x,\lambda a_y,\lambda a_z) λα=(λax,λay,λaz)。
二. 数量积、向量积、混合积
1. 两向量的数量积(也称“点乘”或“内积”)
数量积,即积完之后是一个数。
- 几何表示: a ⃗ ⋅ b ⃗ = ∣ a ⃗ ∣ ∣ b ⃗ ∣ cos θ \vec{a}\cdot \vec{b}=|\vec{a}||\vec{b}|\cos\theta a⋅b=∣a∣∣b∣cosθ,其中, cos θ \cos\theta cosθ为 a ⃗ 与 b ⃗ \vec{a}与\vec{b} a与b的夹角。
- 代数运算:设 a ⃗ = ( a x , a y , a z ) , b ⃗ = ( b x , b y , b z ) , 则 a ⃗ ⋅ b ⃗ = a x b x + a y b y + a z b z \vec{a}=(a_x,a_y,a_z),\vec{b}=(b_x,b_y,b_z),则\vec{a}\cdot\vec{b}=a_xb_x+a_yb_y+a_zb_z a=(ax,ay,az),b=(bx,by,bz),则a⋅b=axbx+ayby+azbz。
- 运算规律: a ⃗ ⋅ b ⃗ = b ⃗ ⋅ a ⃗ ; ( a ⃗ + b ⃗ ) ⋅ c ⃗ = a ⃗ ⋅ c ⃗ + b ⃗ ⋅ c ⃗ \vec{a}\cdot\vec{b}=\vec{b}\cdot\vec{a};(\vec{a}+\vec{b})\cdot\vec{c}=\vec{a}\cdot\vec{c}+\vec{b}\cdot\vec{c} a⋅b=b⋅a;(a+b)⋅c=a⋅c+b⋅c。
- 应用:判断垂直, a ⃗ ⊥ b ⃗ ⇔ a ⃗ ⋅ b ⃗ = 0 ⇔ a x b x + a y b y + a z b z = 0 \vec{a}\perp\vec{b}\Leftrightarrow \vec{a}\cdot\vec{b}=0\Leftrightarrow a_xb_x+a_yb_y+a_zb_z=0 a⊥b⇔a⋅b=0⇔axbx+ayby+azbz=0
2. 两向量的向量积(也称“叉乘”)
顾名思义,积完之后是一个向量。
- 几何表示: ∣ ∣ a ⃗ × b ⃗ ∣ ∣ 2 = ∣ ∣ a ⃗ ∣ ∣ 2 ∣ ∣ b ⃗ ∣ ∣ 2 sin θ ||\vec a\times\vec b||_2=||\vec{a}||_2||\vec{b}||_2\sin\theta ∣∣a×b∣∣2=∣∣a∣∣2∣∣b∣∣2sinθ其中, θ \theta θ是 a ⃗ \vec a a与 b ⃗ \vec b b的夹角, 0 ≤ θ ≤ π 0\le\theta\le\pi 0≤θ≤π,叉乘结果同时垂直向量 a ⃗ \vec a a和 b ⃗ \vec b b。
- 代数表示:设 a ⃗ = ( a x , a y . a z ) , b ⃗ = ( b x , b y , b z ) \vec a=(a_x,a_y.a_z),\vec b=(b_x,b_y,b_z) a=(ax,ay.az),b=(bx,by,bz),则 a ⃗ × b ⃗ = ∣ i ⃗ j ⃗ k ⃗ a x a y a z b x b y b z ∣ \vec a\times\vec b=\begin{vmatrix}\vec i & \vec j & \vec k \\ a_x & a_y & a_z \\ b_x & b_y & b_z \end{vmatrix} a×b=∣∣∣∣∣∣iaxbxjaybykazbz∣∣∣∣∣∣
- 有没有想过为什么是这样呢?这是根据他的几何意义造出来的,如果 ( a ⃗ × b ⃗ ) (\vec a\times\vec b) (a×b)和 a ⃗ \vec a a做点乘(数量积)或 ( a ⃗ × b ⃗ ) (\vec a\times\vec b) (a×b)和 b ⃗ \vec b b做点乘,则会产生以下的结果: ( a ⃗ × b ⃗ ) ⋅ a ⃗ = ∣ a x a y a z a x a y a z b x b y b z ∣ = 0 (\vec a\times \vec b)\cdot\vec a=\begin{vmatrix} a_x & a_y & a_z \\ a_x & a_y & a_z \\ b_x & b_y & b_z \end{vmatrix}=0 (a×b)⋅a=∣∣∣∣∣∣axaxbxayaybyazazbz∣∣∣∣∣∣=0 ( a ⃗ × b ⃗ ) ⋅ b ⃗ = ∣ b x b y b z a x a y a z b x b y b z ∣ = 0 (\vec a\times \vec b)\cdot\vec b=\begin{vmatrix} b_x & b_y & b_z \\ a_x & a_y & a_z \\ b_x & b_y & b_z \end{vmatrix}=0 (a×b)⋅b=∣∣∣∣∣∣bxaxbxbyaybybzazbz∣∣∣∣∣∣=0因为行列式中某两行元素成比例或相等,则行列式等于0。
从而说明 ( a ⃗ × b ⃗ ) (\vec a\times\vec b) (a×b)和 a ⃗ , b ⃗ \vec a,\vec b a,b都垂直,即垂直于 a ⃗ , b ⃗ \vec a,\vec b a,b组成的平面。 - 那 sin θ \sin\theta sinθ为什么是怎么推出来的呢?这里从略,我不太理解,累了。
- 有没有想过为什么是这样呢?这是根据他的几何意义造出来的,如果 ( a ⃗ × b ⃗ ) (\vec a\times\vec b) (a×b)和 a ⃗ \vec a a做点乘(数量积)或 ( a ⃗ × b ⃗ ) (\vec a\times\vec b) (a×b)和 b ⃗ \vec b b做点乘,则会产生以下的结果: ( a ⃗ × b ⃗ ) ⋅ a ⃗ = ∣ a x a y a z a x a y a z b x b y b z ∣ = 0 (\vec a\times \vec b)\cdot\vec a=\begin{vmatrix} a_x & a_y & a_z \\ a_x & a_y & a_z \\ b_x & b_y & b_z \end{vmatrix}=0 (a×b)⋅a=∣∣∣∣∣∣axaxbxayaybyazazbz∣∣∣∣∣∣=0 ( a ⃗ × b ⃗ ) ⋅ b ⃗ = ∣ b x b y b z a x a y a z b x b y b z ∣ = 0 (\vec a\times \vec b)\cdot\vec b=\begin{vmatrix} b_x & b_y & b_z \\ a_x & a_y & a_z \\ b_x & b_y & b_z \end{vmatrix}=0 (a×b)⋅b=∣∣∣∣∣∣bxaxbxbyaybybzazbz∣∣∣∣∣∣=0因为行列式中某两行元素成比例或相等,则行列式等于0。
- 运算规律: a ⃗ × b ⃗ = − ( b ⃗ × a ⃗ ) ( a ⃗ + b ⃗ ) × c ⃗ = a ⃗ × c ⃗ + b ⃗ × c ⃗ \vec a\times\vec b=-(\vec b\times\vec a)\\ (\vec a+\vec b)\times \vec c=\vec a\times\vec c+\vec b\times\vec c a×b=−(b×a)(a+b)×c=a×c+b×c
- 应用:判断两向量是否平行 a ⃗ ∥ b ⃗ ⇔ a ⃗ × b ⃗ = 0 ⇔ a x b x = a y b y = a z b z \vec a\parallel\vec b\Leftrightarrow\vec a\times\vec b=\bm 0\Leftrightarrow\frac{a_x}{b_x}=\frac{a_y}{b_y}=\frac{a_z}{b_z} a∥b⇔a×b=0⇔bxax=byay=bzaz
3. 混合积
- 定义:称 ( a ⃗ × b ⃗ ) ⋅ c ⃗ (\vec a\times \vec b)\cdot\vec c (a×b)⋅c为三个向量的混合积。
设 a ⃗ = ( a x , a y , a z ) , b ⃗ = ( b x , b y , b z ) \vec a=(a_x,a_y,a_z),\vec b=(b_x,b_y,b_z) a=(ax,ay,az),b=(bx,by,bz),则
( a ⃗ × b ⃗ ) ⋅ c ⃗ = ∣ c x c y c z a x a y a z b x b y b z ∣ = ∣ a x a y a z b x b y b z c x c y c z ∣ \begin{aligned} (\vec a\times \vec b)\cdot\vec c&=\begin{vmatrix} c_x & c_y & c_z \\ a_x & a_y & a_z \\ b_x & b_y & b_z \end{vmatrix}\\ \\ &=\begin{vmatrix} a_x & a_y & a_z \\ b_x & b_y & b_z\\c_x & c_y & c_z \end{vmatrix} \end{aligned} (a×b)⋅c=∣∣∣∣∣∣cxaxbxcyaybyczazbz∣∣∣∣∣∣=∣∣∣∣∣∣axbxcxaybycyazbzcz∣∣∣∣∣∣ - 应用:判断三个向量共面。 a ⃗ , b ⃗ , c ⃗ \vec a,\vec b,\vec c a,b,c三点共面 ⇔ ( a ⃗ × b ⃗ ) ⋅ c ⃗ = 0 \Leftrightarrow(\vec a\times \vec b)\cdot\vec c=0 ⇔(a×b)⋅c=0
三. 平面及其方程
平面是由一个定点和法向量进行确定.
1.
- 平面的点法式方程 A ( x − x 0 ) + B ( y − y 0 ) + C ( z − z 0 ) = 0 A(x-x_0)+B(y-y_0)+C(z-z_0)=0 A(x−x0)+B(y−y0)+C(z−z0)=0这里的 ( x 0 , y 0 , z 0 ) (x_0,y_0,z_0) (x0,y0,z0)为平面上一定点, n ⃗ = ( A , B , C ) \vec n=(A,B,C) n=(A,B,C)为平面的法向量。
- 平面的一般式方程 A x + B y + C z + D = 0 Ax+By+Cz+D=0 Ax+By+Cz+D=0这里的 n ⃗ = ( A , B , C ) \vec n=(A,B,C) n=(A,B,C)为平面的法向量。
- 平面的截距式方程 x a + y b + z c = 1 \frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1 ax+by+cz=1显然,这里的 a , b , c a,b,c a,b,c分别为平面在三个坐标轴上的距离, n ⃗ = ( 1 a , 1 b , 1 c ) \vec n=(\frac{1}{a},\frac{1}{b},\frac{1}{c}) n=(a1,b1,c1)为平面的法向量。
2. 平面与平面的特殊位置关系
- 垂直:利用法向量也垂直进行判断,即法向量的数量积(点乘)为零。
- 平行:利用法向量也平行进行判断,即法向量的向量积(叉乘)为零。
四. 空间直线及其方程
空间直线有一个定点和方向向量确定,与直线平行的非零向量称为他的方向向量.
1. 空间直线的点向式方程
x − x 0 m = y − y 0 n = z − z 0 p \frac{x-x_0}{m}=\frac{y-y_0}{n}=\frac{z-z_0}{p} mx−x0=ny−y0=pz−z0
这里的 ( x 0 , y 0 , z 0 ) (x_0,y_0,z_0) (x0,y0,z0)为直线上一定点, s ⃗ = ( m , n , p ) \vec s=(m,n,p) s=(m,n,p)为直线的方向向量。
2. 空间直线的参数式方程
这是由“点向式”方程推导而来的。
{ x = x 0 + m t y = y 0 + n t z = z 0 + p t \left\{\begin{matrix} x=x_0+{\rm m}t\\ y=y_0+{\rm n}t\\ z=z_0+{\rm p}t \end{matrix}\right. ⎩⎨⎧x=x0+mty=y0+ntz=z0+pt
这里的 ( x 0 , y 0 , z 0 ) (x_0,y_0,z_0) (x0,y0,z0)为直线上一定点, s ⃗ = ( m , n , p ) \vec s=(m,n,p) s=(m,n,p)为直线的方向向量。
3. 空间直线的一般式方程
{ A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 \left\{\begin{matrix} A_1x+B_1y+C_1z+D_1=0 \\ A_2x+B_2y+C_2z+D_2=0 \end{matrix}\right. {A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0这里的直线为两平面的交线,方向向量 s ⃗ = n 1 ⃗ × n 2 ⃗ \vec s=\vec{n_1}\times\vec{n_2} s=n1×n2.(叉乘)
五. 一组距离公式
- 点 P 0 = ( x 0 , y 0 , z 0 ) \rm P_0=(x_0,y_0,z_0) P0=(x0,y0,z0)到平面 A x + B y + C z + D = 0 Ax+By+Cz+D=0 Ax+By+Cz+D=0的距离: d = ∣ A x 0 + B y 0 + C z 0 + D ∣ A 2 + B 2 + C 2 d=\frac{|Ax_0+By_0+Cz_0+D|}{\sqrt{A^2+B^2+C^2}} d=A2+B2+C2∣Ax0+By0+Cz0+D∣下面进行证明:
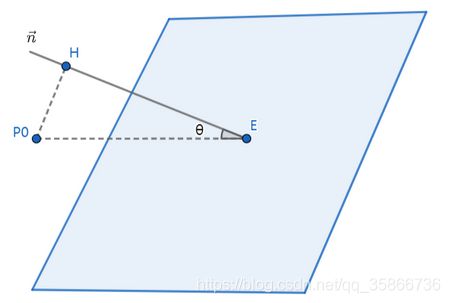
图中 E = ( e 1 , e 2 , e 3 ) E=(e_1,e_2,e_3) E=(e1,e2,e3)为平面上一定点, n ⃗ = ( A , B , C ) \vec n=(A,B,C) n=(A,B,C)为平面法向量, P 0 P_0 P0为平面外一点, P 0 H ⟶ ⊥ n ⃗ \overset{\longrightarrow}{P_0H}\perp\vec n P0H⟶⊥n,则 P 0 P_0 P0到平面的距离为 ∣ ∣ E H ⟶ ∣ ∣ 2 ||\overset{\longrightarrow}{EH}||_2 ∣∣EH⟶∣∣2,由数量积的几何表示可知, E P 0 ⟶ ⋅ n ⃗ = ∣ ∣ E P 0 ⟶ ∣ ∣ 2 ∣ ∣ n ⃗ ∣ ∣ 2 cos θ \overset{\longrightarrow}{EP_0}\cdot\vec n=||\overset{\longrightarrow}{EP_0}||_2||\vec n||_2\cos\theta EP0⟶⋅n=∣∣EP0⟶∣∣2∣∣n∣∣2cosθ,我们知道, n ⃗ ⋅ ( − E ) = D \vec n\cdot (-E)=D n⋅(−E)=D,故 n ⃗ ⋅ ( x 0 − e 1 , y 0 − e 2 , z 0 − e 3 ) = A x 0 + B y 0 + C z 0 + D \vec n\cdot(x_0-e_1,y_0-e_2,z_0-e_3)=Ax_0+By_0+Cz_0+D n⋅(x0−e1,y0−e2,z0−e3)=Ax0+By0+Cz0+D,故 cos θ = A x 0 + B y 0 + C z 0 + D ∣ ∣ E P 0 ⟶ ∣ ∣ 2 ∣ ∣ n ⃗ ∣ ∣ 2 \cos\theta=\frac{Ax_0+By_0+Cz_0+D}{||\overset{\longrightarrow}{EP_0}||_2||\vec n||_2} cosθ=∣∣EP0⟶∣∣2∣∣n∣∣2Ax0+By0+Cz0+D故
d = ∣ ∣ H E ⟶ ∣ ∣ 2 = ∣ ∣ E P 0 ⟶ ∣ ∣ 2 cos θ = A x 0 + B y 0 + C z 0 + D ∣ ∣ n ⃗ ∣ ∣ 2 = A x 0 + B y 0 + C z 0 + D A 2 + B 2 + C 2 \begin{aligned} d&=||\overset{\longrightarrow}{HE}||_2\\ &=||\overset{\longrightarrow}{EP_0}||_2\cos\theta\\ &=\frac{Ax_0+By_0+Cz_0+D}{||\vec n||_2}\\ &=\frac{Ax_0+By_0+Cz_0+D}{\sqrt{A^2+B^2+C^2}} \end{aligned} d=∣∣HE⟶∣∣2=∣∣EP0⟶∣∣2cosθ=∣∣n∣∣2Ax0+By0+Cz0+D=A2+B2+C2Ax0+By0+Cz0+D
为了保证距离是非负数,需要加绝对值,即
d = = ∣ A x 0 + B y 0 + C z 0 + D ∣ A 2 + B 2 + C 2 d==\frac{|Ax_0+By_0+Cz_0+D|}{\sqrt{A^2+B^2+C^2}} d==A2+B2+C2∣Ax0+By0+Cz0+D∣证毕! - 点 P 0 = ( x 0 , y 0 , z 0 ) \rm P_0=(x_0,y_0,z_0) P0=(x0,y0,z0)到空间直线 x − x 1 m = y − y 1 n = z − z 1 p \frac{x-x_1}{m}=\frac{y-y_1}{n}=\frac{z-z_1}{p} mx−x1=ny−y1=pz−z1的距离: d = ∣ ∣ P 0 P ⟶ × s ⃗ ∣ ∣ 2 ∣ ∣ s ⃗ ∣ ∣ 2 d=\frac{||\overset{\longrightarrow}{P_0P}\times \vec s||_2}{||\vec s||_2} d=∣∣s∣∣2∣∣P0P⟶×s∣∣2这里的 P P P是直线上任意一点, s ⃗ = ( m , n , p ) \vec s=(m,n,p) s=(m,n,p)是直线上的方向向量。
证明:

由向量叉乘(向量积)的几何意义可知: ∣ ∣ P 0 P ⟶ × s ⃗ ∣ ∣ 2 = ∣ ∣ P 0 P ⟶ ∣ ∣ 2 ∣ ∣ s ⃗ ∣ ∣ 2 sin θ ||\overset{\longrightarrow}{P_0P}\times \vec s||_2=||\overset{\longrightarrow}{P_0P}||_2||\vec s||_2\sin\theta ∣∣P0P⟶×s∣∣2=∣∣P0P⟶∣∣2∣∣s∣∣2sinθ,从而有
∣ ∣ P 0 P ⟶ × s ⃗ ∣ ∣ 2 ∣ ∣ s ⃗ ∣ ∣ 2 = ∣ ∣ P 0 P ⟶ ∣ ∣ 2 sin θ = ∣ ∣ P 0 H ∣ ∣ 2 = d \frac{||\overset{\longrightarrow}{P_0P}\times \vec s||_2}{||\vec s||_2}=||\overset{\longrightarrow}{P_0P}||_2\sin\theta=||P_0H||_2=d ∣∣s∣∣2∣∣P0P⟶×s∣∣2=∣∣P0P⟶∣∣2sinθ=∣∣P0H∣∣2=d
得证!
六. 曲面及其方程
三元方程 F ( x , y , z ) = 0 {\rm F}(x,y,z)=0 F(x,y,z)=0在空间里面表示一张曲面 S \rm S S,叫做曲面的一般式。
平面是一种特殊的曲面。
1. 旋转曲面
平面上的曲线(母线)绕其平面上的一条直线(轴)旋转一周所形成的曲面叫做旋转曲面。
设 y o z yoz yoz坐标面上的一条曲线 L : { f ( y , z ) = 0 x = 0 L:\left\{\begin{matrix}f(y,z)=0\\ x=0 \end{matrix}\right. L:{f(y,z)=0x=0
- 绕 z z z轴旋转一周所得旋转曲面的方程为: f ( ± x 2 + y 2 , z ) = 0 f(\pm\sqrt{x^2+y^2},z)=0 f(±x2+y2,z)=0;
- 绕 y y y轴旋转一周所得旋转曲面的方程为: f ( y , ± x 2 + z 2 ) = 0 f(y,\pm\sqrt{x^2+z^2})=0 f(y,±x2+z2)=0;
由此可见,三维图形是由二维图形堆叠而成,研究明白二维图形以及二维怎样堆叠为三维图形,就能真正领会三维图形的机理。
2. 柱面的概念
柱面的关键是其无限长。空间解析几何中,缺少字母的方程都是柱面。
