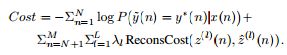阶梯网络Ladder Network

在这里主要讲一下用于半监督学习的ladder network。网上别人分享的资料太少了，也不知道对不对，下面内容请带着怀疑的角度阅读，如有问题，欢迎指出。

在讲半监督学习之前，先简单聊聊监督学习。

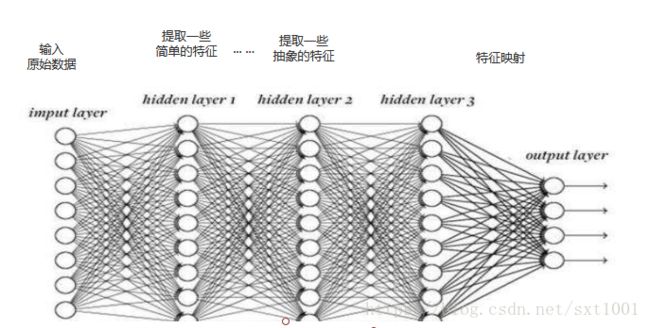
在监督学习中，我们将原始数据通过简单的预处理（标准化等等），然后输入网络，神经网络自己从数据中学习，中间隐藏层就相当于一个个特征提取器。

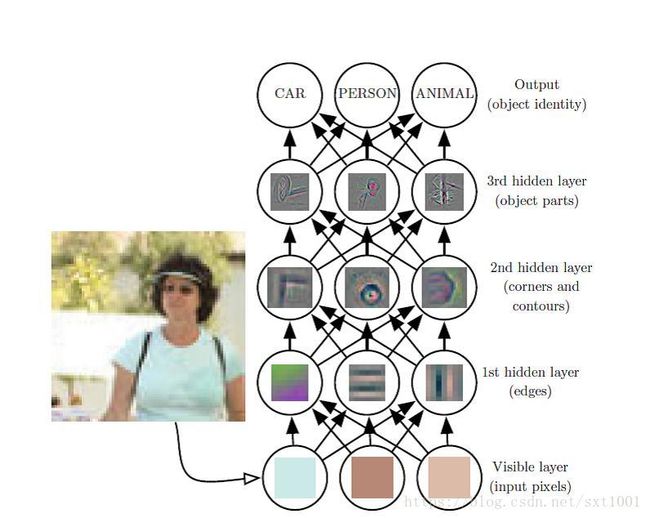
如下图，第一个隐藏层可能会提取一些线条等简单的特征，第二层提取一些由线条组成的轮廓等特征，......,等等，越深层提取的特征越抽象。

我们将最后得到的抽象的特征记为X=（x1,x2,...,xn）。最后，我们通过一个全连接层将这些特征进行映射：f(X) -> y (各个类别的得分）。

在整个网络学习的过程中，神经网络提取与任务有关的信息加以利用，然后却很少利用到那些无用的信息或者直接被过滤掉。

这是监督学习的内容。

 

还有一个领域是无监督学习。在深度学习领域，无监督学习常见的有自编码、受限玻尔兹曼机等。

一般来说，无监督学习的目标函数都是：

无监督学习的目标其实是为了学习原始数据X的另外一种表征X'，同时要保证这个新的特征X',尽可能的能够保留原始数据信息。

 

而我们要聊的半监督学习是一种有监督和无监督相结合的模型。

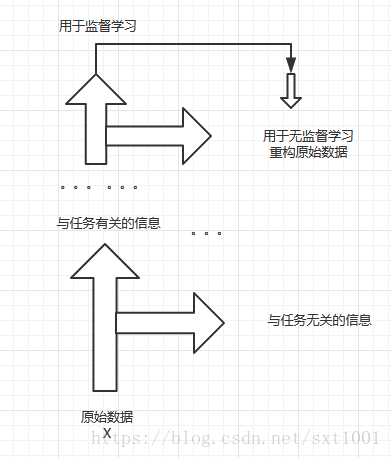
但是无监督学习是要尽可能的保留原始数据的信息，而有监督学习是过滤与任务无关的信息，这个冲突问题使得一直以来有监督学习和无监督学习不能很好的兼容在一起，半监督学习算法不能很好的work。如果我们可以设计一个模型，这个网络有两个分支，可以把监督任务相关的信息和无关的信息尽可能的分开，但同时又都能利用到这些信息就好了。

如下图所示，这也正是阶梯网络的设计思想。

Ladder network阶梯网络：

         当我们有少量的有标签的数据和大量的无标签数据时，形式化表示如下：

1   labeled data:  {(x1,y1),(x2,y2),(x3,y3),...,(xN,yN)}
2  unlabeled data: {(x(N+1,y(N+1)), ... , (x(N+M),y(N+M))}  
这里 M >> N

        此时，我们希望使用上面的数据集来训练得到一个模型p(y|x)，我们就需要用到半监督学习。

       下面简单介绍一下ladder network模型。

      ladder network由2个编码器encoder和1个解码器decoder，它的数学形式如下：

                                                                                 

      在ladder network的编码器部分的每一个编码器类型不局限于多层感知器，我们也可以使用卷积神经网络 or RNN。           

     同时，我们在监督学习中，使用真实标签和预测标签构造loss函数，在无监督学习中，我们使用原始输入X和编码解码后的一种表征X'构造它的loss，在这里我们也可以想到半监督学习模型中的loss函数可能会用到它们两者。ladder network的loss函数形式如下：

                                                                  

        正如论文中介绍的一样，The objective function is a weighted sum of supervised (Cross Entropy) and unsupervised costs (Reconstruction costs).

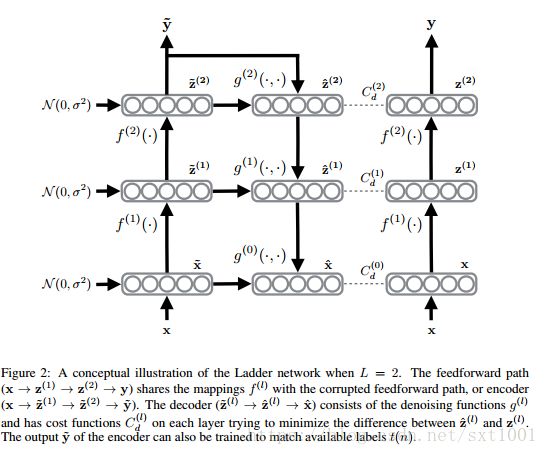
          ladder network的模型结构如下：

                                            

              从图中可以看出，它有2个输出预测标签y~和y,其中the noisy output y~用于loss函数，the noiseless output y 用于测试时的分类任务。

               ladder networkxian详细结构如下：

                               

          算法伪代码如下：

                                                     

废话就这些，也没讲什么。很久没看这个了，就这样。如果想详细了解，可以参考下述论文。

 

1   Semi-Supervised Learning with Ladder Networks，地址：https://arxiv.org/abs/1507.02672

2   Deconstructing the Ladder Network Architecture，地址：https://arxiv.org/abs/1511.06430