回归评价指标(MSE、RMSE、MAE、R-Squared、拟合优度)
文章目录
- 拟合优度
- 均方误差(MSE)
- 均方根误差(RMSE)
- 平均绝对误差(MAE)
- 平均绝对百分比误差(MAPE)
拟合优度
拟合优度(Goodness of Fit)是指回归直线对观测值的拟合程度。度量拟合优度的统计量是可决系数(Coefficient of Determination)R²。可决系数,亦称测定系数、确定系数、决定系数、可决指数。
对于m个样本 ( x 1 → , y 1 ) , ( x 2 → , y 2 ) , ⋯ , ( x m → , y m ) (\overrightarrow{x_{1}},y_{1}),(\overrightarrow{x_{2}},y_{2}),\cdots ,(\overrightarrow{x_{m}},y_{m}) (x1,y1),(x2,y2),⋯,(xm,ym) ,
某模型的估计值为 ( x 1 → , y ^ 1 ) , ( x 2 → , y ^ 2 ) , ⋯ , ( x m → , y ^ m ) (\overrightarrow{x_{1}},\widehat{y}_{1}),(\overrightarrow{x_{2}},\widehat{y}_{2}),\cdots ,(\overrightarrow{x_{m}},\widehat{y}_{m}) (x1,y 1),(x2,y 2),⋯,(xm,y m)
计算样本的总平方和TSS(Total Sum of Squares):
T S S = ∑ i = 1 m ( y i − y ‾ ) 2 TSS=\sum_{i=1}^{m}(y_{i}-\overline{y})^{2} TSS=i=1∑m(yi−y)2
即样本伪方差的m倍 V a r ( Y ) = T S S / m Var(Y)=TSS/m Var(Y)=TSS/m
计算残差平方和RSS(Residual Sum of Squares):
R S S = ∑ i = 1 m ( y i ^ − y i ) 2 RSS=\sum_{i=1}^{m}(\widehat{y_{i}}-y_{i})^{2} RSS=i=1∑m(yi −yi)2
注:RSS即误差平方和SSE(Sum of Squares Error)。
定义 R 2 = 1 − R S S / T S S R^{2}=1-RSS/TSS R2=1−RSS/TSS
注: R 2 R^{2} R2越大,拟合效果越好。 R 2 R^{2} R2的最优值为1,若模型预测为随机值, R 2 R^{2} R2有可能为负值。若预测值恒为样本期望, R 2 R^{2} R2为0。
均方误差(MSE)
MSE (Mean Squared Error)叫做均方误差,真实值-预测值 然后平方之后求和平均,衡量观测值与真实值之间的偏差。
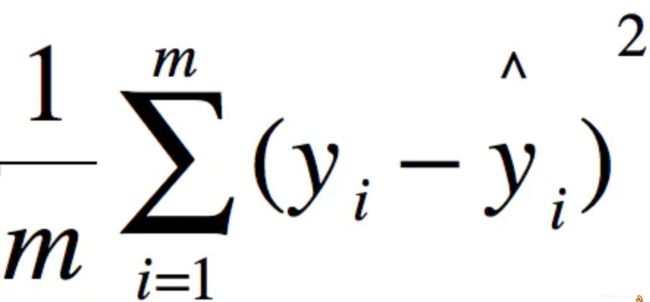
均方根误差(RMSE)
RMSE(Root Mean Squard Error)均方根误差,RMSE其实是MSE开根号,两者实质一样,但RMSE能更好的描述数据。因为MSE单位量级和误差的量级不一样,而RMSE跟数据是一个级别的,级别一样更容易去感知数据。
缺点:易受异常值的影响。

平均绝对误差(MAE)
MAE(Mean Absolute Error)平均绝对误差
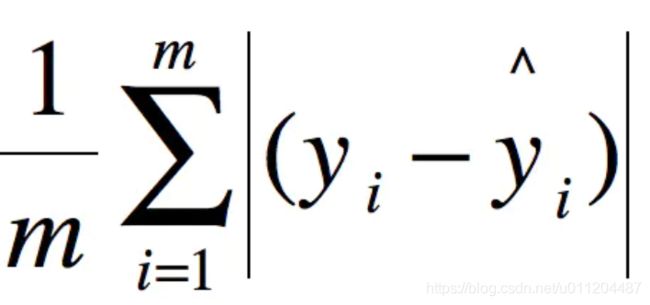
平均绝对百分比误差(MAPE)
平均绝对百分比误差(Mean Absolute Percentage Error),与RMSE相比,更加鲁棒,因为MAPE对每个点的误差进行了归一化。
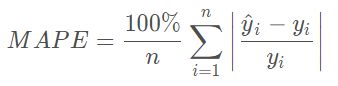
参考:https://blog.csdn.net/guolindonggld/article/details/87856780