简要整理有权单源最短路-Dijkstra(迪杰斯特拉)算法

Dijkstra(迪杰斯特拉)算法
这次整理一下Dijkstra算法.
大部分资料参考数据结构 陈越版
Dijkstra算法是求有权图的单源最短路的算法,是一种按路径长度递增的次序产生最短路径的算法.
Dijkstra算法的核心就是按距离递增顺序逐步找出起点到各个顶点的最短距离.过程类似Prim法求最小生成树,可以参考我的另一篇文章Prim.
这个算法需要三个辅助数组dist[],path[],collected[].
dist数组储存各顶点到起点的最短距离.
path数组记录该顶点(相应的最短路径)邻接与哪个顶点.
collected表示该顶点是否被录入过.

用v0表示起点,vj表示各顶点,graph表示图.
Dijkstra算法的大致过程:
1.找到一个v0,初始化dist为graph的距离,没有连接到的设为INF(无穷大).
2.找到dist中没有被录入并且离v0最短的点v.(贪心)
3.将v录入,修改v有邻接的点,w是被影响的顶点,dist[w]=min{dist[w],dist[w]+},设置path[w]=v(w邻接与v).
(即当通过v到达w比之前的点直接到达w更近的时候更新.)
4.不断重复以上步骤,直到没有点符合条件(可能是所有点都录入也可能有点是独立的).
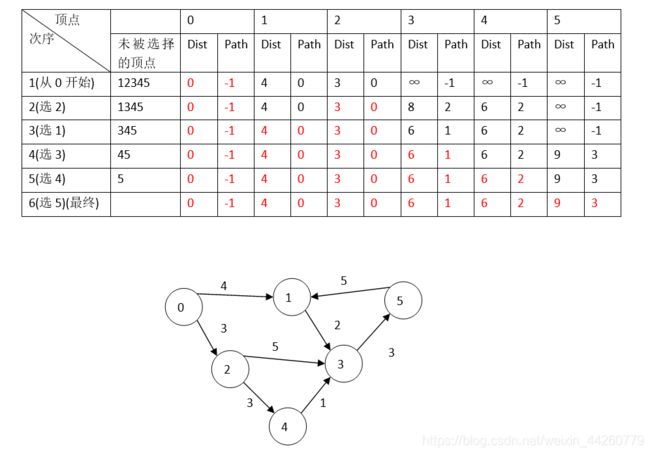
图解:
红色表示已收录,可以直接继承.
每次选未被收录且dist值最小的点.
(案例数据有点粗糙,请理解)

注意点:
1.该算法的时间复杂度取决于返回dist最小值的部分,本文的代码复杂度为O(n²)适用于稠密图,
对于稀疏图建议使用最小堆,时间复杂度为O(nlogn).
2.不能解决带负边的图.
3.一个点被录入后就一定是最小值,不会随着其它点录入而改变(设v是先录入的,如果w录入会导致v变小,那么w应该比v先录入).
4.最终结果可能不唯一,可能dist相同但path不同.

具体实现代码:
选自慕课的陈越老师的数据结构
(此为部分关键代码,部分声明没有给出)
(所有细节都写在代码注释上了,应该不难理解)

/* 邻接矩阵存储 - 有权图的单源最短路算法 */
// MGraph是邻接矩阵类型 
Vertex FindMinDist( MGraph Graph, int dist[], int collected[] )
{ /* 返回未被收录顶点中dist最小者 */
    Vertex MinV, V;
    int MinDist = INFINITY;//设为正无穷大 
 // Graph->Nv是图顶点的数量 
    for (V=0; V<Graph->Nv; V++) {//遍历所有的边 
        if ( collected[V]==false && dist[V]<MinDist) { 
            /* 若V未被收录，且dist[V]更小 */
            MinDist = dist[V]; /* 更新最小距离 */
            MinV = V; /* 更新对应顶点 */
        }
    }
    if (MinDist < INFINITY) /* 若找到最小dist */
        return MinV; /* 返回对应的顶点下标 */
    else return ERROR;  /* 若这样的顶点不存在，返回错误标记 */ 
}
 
bool Dijkstra( MGraph Graph, int dist[], int path[], Vertex S )
{
    int collected[MaxVertexNum];
    Vertex V, W;
 
    /* 初始化：此处默认邻接矩阵中不存在的边用INFINITY表示 */
    for ( V=0; V<Graph->Nv; V++ ) {
        dist[V] = Graph->G[S][V];
        if ( dist[V]<INFINITY )
            path[V] = S;
        else
            path[V] = -1;
        collected[V] = false;
    }
    /* 先将起点收入集合 */
    dist[S] = 0;
    collected[S] = true;
 
    while (1) {
        /* V = 未被收录顶点中dist最小者 */
        V = FindMinDist( Graph, dist, collected );
        if ( V==ERROR ) /* 若这样的V不存在 */
            break;      /* 算法结束 */
        collected[V] = true;  /* 收录V */
        for( W=0; W<Graph->Nv; W++ ) /* 对图中的每个顶点W */
            /* 若W是V的邻接点并且未被收录 */
            if ( collected[W]==false && Graph->G[V][W]<INFINITY ) {
                if ( Graph->G[V][W]<0 ) /* 若有负边 */
                    return false; /* 不能正确解决，返回错误标记 */
                /* 若收录V使得dist[W]变小 */
                if ( dist[V]+Graph->G[V][W] < dist[W] ) {
                    dist[W] = dist[V]+Graph->G[V][W]; /* 更新dist[W] */
                    path[W] = V; /* 更新S到W的路径 */
                }
            }
    } /* while结束*/
    return true; /* 算法执行完毕，返回正确标记 */
}

初学者可以去看慕课看相关的视频,Dijkstra.
手写,最基本的代码:

#include
using namespace std;
int map[105][105];
#define inf 99999999
int dist[105];
int visit[105];
int main()
{
    int n,m;//输入顶点数和道路数 
    while(cin>>n>>m,n||m)
    { 
        for(int i=1;i<=n;i++)//初始化地图 
        for(int j=1;j<=n;j++)
        map[i][j]=inf;
        
        int a,b,c;
        for(int i=0;i<m;i++)//输入道路 
        {
            cin>>a>>b>>c;
            map[a][b]=map[b][a]=c;
        }
        
        for(int i=2;i<=n;i++)//初始化数据 
        {
            dist[i]=map[1][i];
            visit[i]=0;
        }
        dist[1]=0;//录入第一个顶点 
        visit[1]=1;
        while(1)
        {
            int min=inf;
            int v=0;
            for(int i=2;i<=n;i++) 
            {//找到未被录入且dist最小的点 
                if(dist[i]<min&&visit[i]==0)
                {
                    min=dist[i];
                    v=i;
                }
            }
            if(v==0)
            break;
            visit[v]=1;//录入v 
            for(int i=2;i<=n;i++)
            {
                if(map[v][i]<inf&&visit[i]==0)
                {//更新v可能影响的点 
                    if(dist[i]>dist[v]+map[v][i]) 
                    {
                        dist[i]=dist[v]+map[v][i];
                    }
                }
            }
            
        }
        cout<<dist[n]<<endl;
    }
    return 0;
}

简单的案例题 杭电2544最短路.
杭电2544最短路解析
由于能力问题,这篇文章可能有点错误或不足,欢迎评论指出.