【编译原理】中间代码优化(一) 优化技术大观

代码优化概述.

通过对程序进行等价变换，使得从变换后的程序出发，能够生成更加有效的目标代码，这种变换我们叫做优化。

优化其实可以在编译的各个阶段进行，但最主要的一类优化是在目标代码生成以前，对语法分析、语义分析后产生的中间代码进行优化。这是因为中间代码的形式不依赖于具体的计算机，它可以是三地址码的形式，所以相应的对于中间代码的优化也不依赖于具体的计算机。另一类优化是在生成目标代码时进行的，它很大程序上依赖于具体的计算机。
中间代码的优化中，有很多技术和手段可以应用。大局上来说，中间代码优化器的位置如下图所示：

【下图引用自中南大学徐德智老师的编译原理2020年授课PPT】

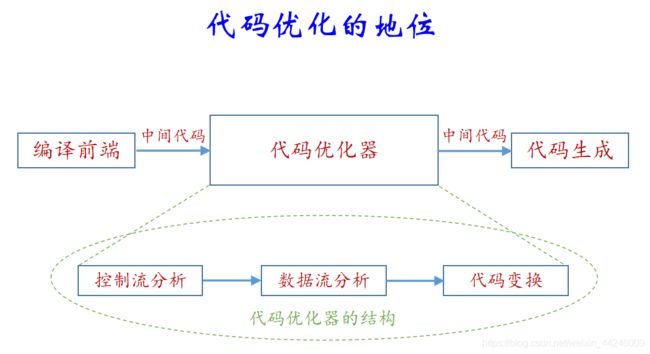
其中编译前端就是词法分析、语法分析、语义分析以及中间代码生成这些阶段。有的优化工作很容易实现，比如基本块内的局部优化。在一个程序运行时，相当一部分的时间是花在循环代码上的，因此基于循环的优化是极其重要的。而有的优化技术涉及对整个程序的控制流、数据流分析，其实现代价是相当高的。
我们进行中间代码优化的目的是为了产生更加高效的代码，所以由代码优化器提供的，对代码的各种变化必须要遵循一定的原则，一切为了更高效的代码。

• 等价原则：经过优化后不应该改变程序运行的结果。这是最不应该也不能破坏的原则，试问程序结果都不正确了，优化的意义何在？
• 有效原则：优化后的代码运行快、存储空间需求小。这也正是我们优化代码的目的，从时空两个维度尽可能让代码效率高。
• 合算原则：尽可能以较低的代价，取得较高的优化效果。

优化可以从各个环节着手。首先，在源代码层面，程序员通过选择适当的高效算法，安排适当的实现语句来提高程序的效率。例如，归并排序肯定要比直接插入排序在绝大多数情况下的效率更高，执行时间更短吧；其次，在设计语义动作时，我们不仅可以考虑产生更加高效的中间代码，还可以在语义分析阶段为优化做一些预备工作。例如，为循环代码的begin和end对应的中间代码“打上标记”，这样有助于后续的控制流、数据流分析；代码的分叉处和交汇处(通常是条件判断语句控制)也“打上标记”，这样有助于识别程序流图中的直接前驱和直接后继。对于编译产生的中间代码，我们安排专门的优化阶段，进行各种等价变换，以提高代码的工作效率。而在目标代码这一层面，我们应该考虑如何有效地利用寄存器，如何选择指令以及如何进行窥孔优化等。

窥孔优化，顾名思义，是一种很局部的优化方式，编译器仅仅在一个基本块或者多个基本块中，针对已经生成的代码，结合CPU自己指令的特点，通过一些认为可能带来性能提升的转换规则，或者通过整体的分析，通过指令转换，提升代码性能。别看这些代码转换很局部，很小，但可能会带来很大的性能提升。这个窥孔，你可以认为是一个滑动窗口，编译器在实施窥孔优化时，就仅仅分析这个窗口内的指令。每次转换之后，可能还会暴露相邻窗口之间的某些优化机会，所以可以多次调用窥孔优化，尽可能提升性能。

中间代码优化全局大观.

上面我们说完了代码优化的地位、原因以及目标，接下来我们通过一段中间代码实例以及它从最初到优化完成的过程，来展示、介绍中间代码优化具体做了哪些事。首先我们给出这段中间代码的最初状态：

【下图引用自中南大学徐德智老师的编译原理2020年授课PPT】

图中是中间代码的基本块程序流图展示，至于基本块如何划分，我们后面会给出算法，这里并不是问题的重点。我们是要看，究竟代码优化器，对这样的中间代码，做了怎样的等价变换。

1.删除公共子表达式(Common Subexpressions Elimination).

对于一个表达式E，如果它的值在前面已经计算过，并且在这之后E中变量的值并没有发生过改变(至于常量值更是无法改变了，不要ETC)，那我们就称这样的表达式E为公共子表达式。对于这样的公共子表达式，我们可以避免对它的重复计算，而全部使用E中已经计算出的结果，称为删除公共子表达式，有时也称为删除多余运算(因为已经计算过了).

ETC(Electronic Toll Collection)，中文翻译是电子不停车收费系统，是高速公路或桥梁自动收费。通过安装在车辆挡风玻璃上的车载电子标签与在收费站 ETC 车道上的微波天线之间进行的专用短程通讯，利用计算机联网技术与银行进行后台结算处理，从而达到车辆通过高速公路或桥梁收费站无需停车而能交纳高速公路或桥梁费用的目的。

看我们上面给出的中间代码实例，当中哪些是多余运算，或者说公共子表达式呢？着眼于B${}_5$基本块：

T6:=4*i
x:=a[T6]
T7:=4*i
T8:=4*j 
T9:=a[T8]
a[T7]:=T9
T10:=4*j
a[T10]:=x
goto B2

我们可以看到T6和T7这一组，以及T8和T10这一组一共两组临时变量都属于上面提到的公共子表达式。4*i的结果已经被计算了放在T6变量中，那么T7还有计算的必要吗，显然没有。所以针对这部分代码，我们可以修改如下：

T6:=4*i
x:=a[T6]
T7:=T6
T8:=4*j 
T9:=a[T8]
a[T7]:=T9
T10:=T8
a[T10]:=x
goto B2

修改之后我们发现，B${}_5$中只需要分别计算一次4*i和4*j. 我们还可以在更大的范围内来考虑删除公共子表达式的问题。我们注意到B${}_2$中计算了4*i的值并且保存在T2中，而B${}_3$中计算了4*j的值，保存在T4中。并且最关键的是，在这两个地方计算出表达式的值之后，i和j的值一直都没有发生变化，是很标准的公共子表达式(多余运算)。所以B${}_5$中的中间代码可以变换为如下的形式：

T6:=T2
x:=a[T6]
T7:=T6
T8:=T4
T9:=a[T8]
a[T7]:=T9
T10:=T8
a[T10]:=x
goto B2

对于B${}_6$我们也进行一次同样的分析之后，我们可以将中间代码修改为下面这样：

【下图引用自中南大学徐德智老师的编译原理2020年授课PPT】

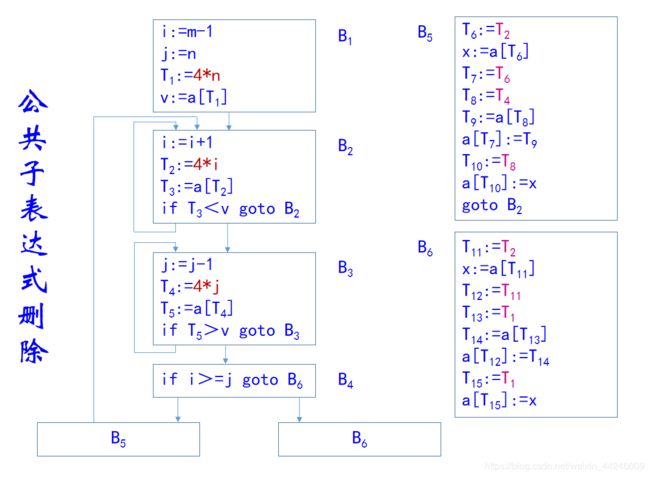
我们可以对比现在的中间代码和最初的中间代码，T1=4*n;T2=4*i;T4=4*j这三个公共子表达式(4*n、4*i、4*j是公共表达式)在B${}_5$和B${}_6$中被优化了，删除了多余运算。

2.复写传播.

上面的中间代码还可以进一步改进，我们还是着眼于B${}_5$来进行分析。T6=T2;x=a[T6]这两条语句中，T6的值并没有发生改变，一直是T2的值，因此可以直接将a[T2]的值赋给x，这种变换称为复写传播。

复写传播（拷贝传播）：某些变量的值并未被改变过便赋给其他变量，则可直接引用原值本身.

通过复写传播的优化方法之后，我们可以将B${}_5$变换为如下中间代码：

T6:=T2
x:=a[T2]
T7:=T2
T8:=T4
T9:=a[T4]
a[T2]:=T9
T10:=T4
a[T4]:=x
goto B2

进一步分析发现，a[T2]的值曾经在B${}_2$中被T3=a[T2]计算过，所以x=a[T2]可以变换为x=T3，进而再一次应用复写传播，将a[T4]=x变换为a[T4]=T3；同样的，因为a[T4]在B${}_3$中被T5=a[T4]计算过，所以T9=a[T4]可以变换为T9=T5，从而也应用复写传播，将a[T2]=T9变换为a[T2]=T5，至此，B${}_5$中的代码变换成了下面的样子：

T6:=T2
x:=T3
T7:=T2
T8:=T4
T9:=T5
a[T2]:=T5
T10:=T4
a[T4]:=T3
goto B2

对B${}_6$也进行同样的分析(其实不难发现，B${}_5$和B${}_6$的代码几乎是对称的，这段代码是快速排序的代码)，我们得到了下面的中间代码：

【下图引用自中南大学徐德智老师的编译原理2020年授课PPT】

复写传播的目的是使得对于某些变量的赋值，变得无用。我们很快就可以看到这一点。

3.删除无用代码.

对于进行了复写传播之后的B${}_5$块进行分析，可以发现变量x以及T6,T8,T9,T10这些临时变量在赋值符号的右边都没有出现过，这就意味着它们的值其实在整个B${}_5$块内自从被赋值之后，就没有使用过，因此这些变量的赋值对于程序的运行结果没有任何作用，有没有都是一样。但对于代码的执行效率来说就不是这样了，可以看出B${}_5$代码段其实是在一个循环块内的，很小的性能累赘乘以循环次数就是很大的效率阻碍了。我们可以删除对于这些变量的赋值代码，从而将B${}_5$转换为下面的代码：

a[T2]:=T5
a[T4]:=T3
goto B2

一下子代码的逻辑清晰明了了许多，之前的代码中那么多赋值颠来倒去，很难看出到底在做什么。删除无用代码之后，不仅效率提高了，代码也清新了许多(虽然我们很少会直接看到中间代码，但代码的清新意味着计算机执行时的快速与高效，这一点比较删除前后的代码，不难看出吧).
同样地，我们对B${}_6$段也进行无用代码的删除，当中的变量x以及临时变量T11,T12,T13,T14,T15的赋值语句都属于无用代码，删除之后的代码如下：

a[T2]:=v
a[T1]:=T3

至此我们可以给出，删除公共子表达式、复写传播和删除无用代码之后的中间代码形式：

【下图引用自中南大学徐德智老师的编译原理2020年授课PPT】

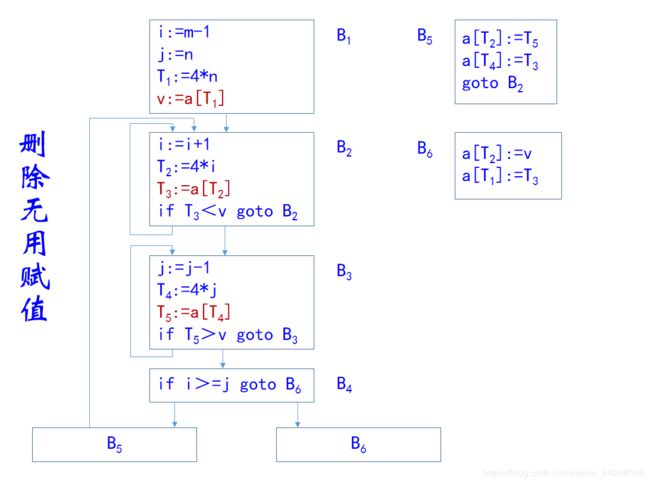
不难看出，前面所介绍的三种优化都是针对某一个基本块内部所作的优化，例如B${}_5$块内的优化就只在块内自己进行，那么下面我们要介绍的优化技术，都是涉及循环的优化。

中间代码优化根据优化所涉及的程序范围分成：

• 局部优化：在程序基本块内进行的优化；
• 循环优化：在程序循环体内进行的优化；
• 全局优化：在整个程序范围内进行的优化。

4.代码外提.

对于循环中的某些代码，如果在整个循环的过程中它产生的结果是不变的，就可以将这部分代码提到循环外去，以免每一次循环都要对这条代码进行运算。例如对于while(i这样的代码，如果limit是一个在循环中没有改变的值，我们完全可以将limit-1提到循环外：
t=limit-1
while(i
这种变换称为代码外提，但在我们这个实例中，循环过程中并没结果不变的代码，所以这一优化步骤跳过。

5.强度削弱与删除归纳变量.

这一优化步骤中我们着眼于基本块B${}_3$。循环每执行一次，j的值-1，而T4始终与j保持着T4=4*j的线性关系，因而每循环一次T4的值-4. 因此我们可以将循环中对于T4的乘法运算，变换为对T4的减法运算。因为计算机中对于加减法的运算比乘除法要快，所以这一技术称为强度削弱。同理对于B${}_2$中的T2变量，我们也可以进行这样的强度削弱。

基本归纳变量——若循环中对 B 只有唯一的递归赋值 B:=B+C 且 C 为循环不变量,则称 B 为循环的基本归纳变量。
归纳变量——若B为基本归纳变量，而A在循环中的定值可以化归为B的线性函数: A:=C1*B+C2(C1,C2为循环不变量)，则称A 为归纳变量,并称 A与 B同族。

根据这里给出的定义，显然i和j就是定义中的基本归纳变量，而T2和T4就是归纳变量。在我们对T2=4*i以及T4=4*j进行强度削弱之后，i和j除了被用于条件判断语句if i>=j goto B6控制跳转之外，不在其他地方被引用，因此我们完全可以删除这里的基本归纳变量i和j，将条件控制语句用T2和T4的值来完成：if T2>=T4 goto B6。所以完成了强度削弱和删除归纳变量之后的中间代码如下所示:

【下图引用自中南大学徐德智老师的编译原理2020年授课PPT】
到这里我们完成了一次中间代码优化，并且了解了代码优化的过程中到底做了哪些事情，以及如何完成这些事情的细节。