Codeforces Round #594 (Div. 1)1239A 【Ivan the Fool and the Probability Theory】题解

Recently Ivan the Fool decided to become smarter and study the probability theory. He thinks that he understands the subject fairly well, and so he began to behave like he already got PhD in that area.

To prove his skills, Ivan decided to demonstrate his friends a concept of random picture. A picture is a field of nn rows and mm columns, where each cell is either black or white. Ivan calls the picture random if for every cell it has at most one adjacent cell of the same color. Two cells are considered adjacent if they share a side.

Ivan’s brothers spent some time trying to explain that it’s not how the randomness usually works. Trying to convince Ivan, they want to count the number of different random (according to Ivan) pictures. Two pictures are considered different if at least one cell on those two picture is colored differently. Since the number of such pictures may be quite large, print it modulo $10^9+7$

Input

The only line contains two integers nn and mm (1≤n,m≤1000001≤n,m≤100000), the number of rows and the number of columns of the field.

Output

Print one integer, the number of random pictures modulo $10^9+7$

Example

Input

Copy

2 3

Output

Copy

8

Note

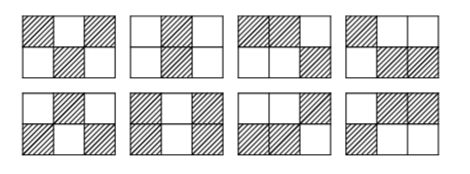
The picture below shows all possible random pictures of size 2 by 3.

---

方程建立过程

首先分析题目要求，一个n*m的网格图，每个格子可以染黑色、白色，其中每个格子最多有一个相邻颜色相同，求满足条件的方案数。

通过观察样例可以得出一个规律

相邻两行的颜色要么完全相同，要么完全相反

---

以下情景只考虑黑色染色一种情况，最后X2则为答案

首先考虑没有相邻格子颜色相同的情况。也就是黑白相间的情况。仔细分析之后就会发现，就是下面这个玩意儿。

​ 国际象棋（图源百度百科）

由上图可以得知，没有相同颜色相邻的染色方案有且只有一种。

接下来我们推导有相同颜色相邻的情况。

我们以3X3方格为例

对其分析可知，我们只对第一行进行填充，不难发现

当第一行存在颜色相连的情况时，第二行必然和第一行完全相反,……第n行和第（n-1）行相反

意思就是当我们确定第一行的染色方式之后，整张图的染色方式就已经确定

所以现在我们将本问题缩减为了

求出第一行染色方案的个数

---

接下来我们想办法对此问题进行公式化。

我们知道，若第i个格子为黑色的条件是，第i-1个格子和第i-2个格子不能同时为黑色。即为第i-1和i-2个只能有一个和第i个同时为黑色

我们建立一个递推公式
$$f[i][0]为有i个格子时第i个格子染色为黑色的情况$$

$$反之f[i][1]为有i个格子时第i个格子染色为白色的情况$$

我们通过分析可以推出公式
$$f[i][0]=f[i-1][0]+f[i-2][0]$$

$$f[i][1]=f[i-1][1]+f[i-2][1]$$

合并两式
$$f[i]=f[i][0]+f[i][1]$$
可得
$$f[i]=f[i-1]+f[i-2]$$
我们在这里求出的f[i]则为当前行有i格时的染色方案数。

那么现在问题解决了吗？

仔细想一想

---

第一列染色方案数又为多少？

通过上述推导过程的结论之一

当第一行存在颜色相连的情况时，第二行必然和第一行完全相反,……第n行和第（n-1）行相反

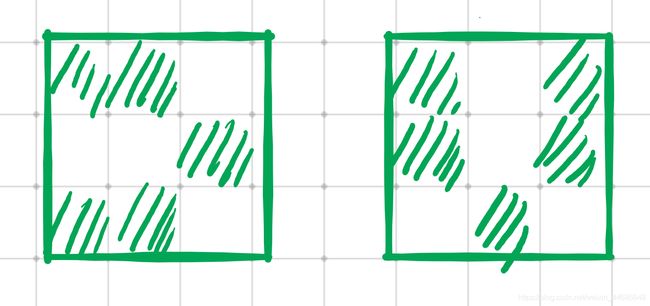
我们不难得出，第一行所包含的染色方案任意一列的不同行颜色必为黑白间隔。即为下图的情况

左图为上述模块我们考虑到的情况之一，但是右图的染色方案也是完全合法的，我们并没有将其考虑进去。

”仿照上例显然“-----《西江月·证明》

当我们确定第一列的染色方式之后，整张图的染色方式就已经确定

即为第一列的染色方案数为f[row]。

---

马上就是答案了！

由上述推导可得目前的染色方案数为（f[row]+f[column])

那么他们是否有交集呢？

我们回到上一模块的开头，我们进行染色方案的推导时，是以

当第一行（列）存在颜色相连的情况时，第二行（列）必然和第一行（列）完全相反,……第n行（列）和第（n-1）行（列）相反

为基础进行推导的。

这玩意什么意思呢？意思就是我们通过第一行确定整个图时，任意一列都不可能出现连续两个颜色相同的情况
反之,通过第一列确定整个图时，任意一行都不可能出现连续两个颜色相同的情况，如同上一模块图中所示，所以我们知道这两个解空间在任意出现过连续两格颜色时没有交集。

所以说呢，他们的交集就是这个玩意儿。。。。。。

是的就是国际象棋棋盘染色法。。。。

所以染色方案共有
$$(f[n]+f[m]-1)种$$
然后我们将配色方案反转得到

最终答案

$$ans=2\ast (f[n]+f[m]-1)$$

---

上代码

#include
const int maxn = 1e5 + 5;
const long long mod = 1e9 + 7;
long long f[maxn];
void fun(int max) {
	f[1] = 1;
	f[2] = 2;
	for (int i = 3; i <=max; i++)
	{
		f[i] = (f[i - 1] + f[i - 2])%mod;
	}
}
int main(void) {
	int n, m;
	scanf("%d%d", &n, &m);
	fun(n>m?n:m);
	printf("%lld\n", (2 * (f[n] + f[m] - 1))%mod);
	return 0;
}

题解完毕，新手上路，如有不足，还望各位在评论区撞死我，蟹蟹！