第3章——排序【冒泡、选择、插入、希尔、归并、快速排序、排序的稳定性等】
文章目录
- 一丶知识点
- 二丶Comparable 接口
- 三丶冒泡排序
- 四丶选择排序
- 五丶插入排序
- 六丶希尔排序
- 七丶归并排序
- 八丶快速排序
- 九丶排序的稳定性
- 十丶测试各大排序法的时间消耗
- 十二丶资料文档
一丶知识点
- Comparable 接口
- 冒泡排序法【简单排序】
- 选择排序法【简单排序】
- 插入排序法【简单排序】
- 希尔排序法【高级排序】
- 归并排序法【高级排序】
- 快速排序法【高级排序】
- 排序的稳定性
2020版数据结构与算法
完整视频:http://yun.itheima.com/course/639.html?2007zzp
配套资料:https://pan.baidu.com/s/1wxKSQw8exCdqFek-VDrSPg 提取码:jkg9
二丶Comparable 接口
由于我们这里要讲排序,所以肯定会在元素之间进行比较,而Java提供了一个接口Comparable就是用来定义排序规则的,在这里我们以案例的形式对Comparable接口做一个简单的回顾。
学生类
//1.定义一个学生类Student,具有年龄age和姓名username两个属性,并通过Comparable接口提供比较规则;
public class Student implements Comparable<Student>{
private String username;
private int age;
public String getUsername() {
return username;
}
public void setUsername(String username) {
this.username = username;
}
public int getAge() {
return age;
}
public void setAge(int age) {
this.age = age;
}
@Override
public String toString() {
return "Student{" +
"username='" + username + '\'' +
", age=" + age +
'}';
}
@Override
public int compareTo(Student o) {
return this.getAge()-o.getAge();
}
}
测试类
//2.定义测试类Test,在测试类Test中定义测试方法Comparable getMax(Comparable c1,Comparable c2)完成测试
public class TestComparable {
public static void main(String[] args) {
//创建两个Student对象,并调用getMax方法,完成测试
Student s1 = new Student();
s1.setUsername("张三");
s1.setAge(18);
Student s2 = new Student();
s2.setUsername("李四");
s2.setAge(20);
Comparable max = getMax(s1, s2);
System.out.println(max);
}
public static Comparable getMax(Comparable c1,Comparable c2){
int result = c1.compareTo(c2);
//如果result<0,则c1比c2小;
//如果result>0,则c1比c2大;
//如果result==0,则c1和c2一样大;
if (result>=0){
return c1;
}else{
return c2;
}
}
}
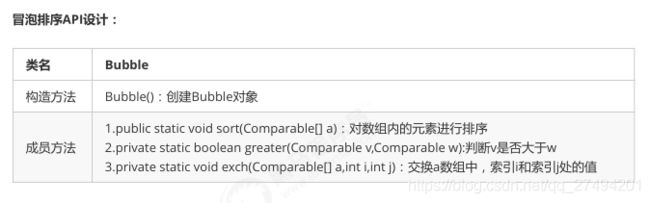
三丶冒泡排序
排序原理:
1. 比较相邻的元素。如果前一个元素比后一个元素大,就交换这两个元素的位置。
2. 对每一对相邻元素做同样的工作,从开始第一对元素到结尾的最后一对元素。最终最后位置的元素就是最大
值。
public class Bubble {
/*
对数组a中的元素进行排序
*/
public static void sort(Comparable[] a){
for(int i=a.length-1;i>0;i--){
for(int j=0;j<i;j++){
//{6,5,4,3,2,1}
//比较索引j和索引j+1处的值
if (greater(a[j],a[j+1])){
exch(a,j,j+1);
}
}
}
}
/*
比较v元素是否大于w元素
*/
private static boolean greater(Comparable v,Comparable w){
return v.compareTo(w)>0;
}
/*
数组元素i和j交换位置
*/
private static void exch(Comparable[] a,int i,int j){
Comparable temp;
temp = a[i];
a[i]=a[j];
a[j]=temp;
}
}
测试类
package cn.itcast.algorithm.test;
import cn.itcast.algorithm.sort.Bubble;
import java.util.Arrays;
public class BubbleTest {
public static void main(String[] args) {
Integer[] arr = {4,5,6,3,2,1};
Bubble.sort(arr);
System.out.println(Arrays.toString(arr));//{1,2,3,4,5,6}
}
}
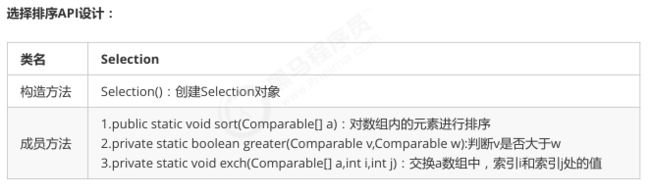
四丶选择排序
排序原理:
1.每一次遍历的过程中,都假定第一个索引处的元素是最小值,和其他索引处的值依次进行比较,如果当前索引处
的值大于其他某个索引处的值,则假定其他某个索引出的值为最小值,最后可以找到最小值所在的索引
2.交换第一个索引处和最小值所在的索引处的值
public class Selection {
/*
对数组a中的元素进行排序
*/
public static void sort(Comparable[] a){
for(int i=0;i<=a.length-2;i++){
//定义一个变量,记录最小元素所在的索引,默认为参与选择排序的第一个元素所在的位置
int minIndex = i;
for(int j=i+1;j<a.length;j++){
//需要比较最小索引minIndex处的值和j索引处的值;
if (greater(a[minIndex],a[j])){
minIndex=j;
}
}
//交换最小元素所在索引minIndex处的值和索引i处的值
exch(a,i,minIndex);
}
}
/*
比较v元素是否大于w元素
*/
private static boolean greater(Comparable v,Comparable w){
return v.compareTo(w)>0;
}
/*
数组元素i和j交换位置
*/
private static void exch(Comparable[] a,int i,int j){
Comparable temp;
temp = a[i];
a[i]=a[j];
a[j]=temp;
}
}
测试类
import java.util.Arrays;
public class SelectionTest {
public static void main(String[] args) {
//原始数据
Integer[] a = {4,6,8,7,9,2,10,1};
Selection.sort(a);
System.out.println(Arrays.toString(a));//{1,2,4,5,7,8,9,10}
}
}
五丶插入排序
排序原理:
1.把所有的元素分为两组,已经排序的和未排序的;
2.找到未排序的组中的第一个元素,向已经排序的组中进行插入;
3.倒叙遍历已经排序的元素,依次和待插入的元素进行比较,直到找到一个元素小于等于待插入元素,那么就把待
插入元素放到这个位置,其他的元素向后移动一位;
public class Insertion {
/*
对数组a中的元素进行排序
*/
public static void sort(Comparable[] a){
for(int i=1;i<a.length;i++){
for(int j=i;j>0;j--){
//比较索引j处的值和索引j-1处的值,如果索引j-1处的值比索引j处的值大,则交换数据,如果不大,那么就找到合适的位置了,退出循环即可;
if (greater(a[j-1],a[j])){
exch(a,j-1,j);
}else{
break;
}
}
}
}
/*
比较v元素是否大于w元素
*/
private static boolean greater(Comparable v,Comparable w){
return v.compareTo(w)>0;
}
/*
数组元素i和j交换位置
*/
private static void exch(Comparable[] a,int i,int j){
Comparable temp;
temp = a[i];
a[i]=a[j];
a[j]=temp;
}
}
测试类
import java.util.Arrays;
public class InsertionTest {
public static void main(String[] args) {
Integer[] a = {4,3,2,10,12,1,5,6};
Insertion.sort(a);
System.out.println(Arrays.toString(a));//{1,2,3,4,5,6,10,12}
}
}
六丶希尔排序
排序原理:
1.选定一个增长量h,按照增长量h作为数据分组的依据,对数据进行分组;
2.对分好组的每一组数据完成插入排序;
3.减小增长量,最小减为1,重复第二步操作。
![]()
public class Shell {
/*
对数组a中的元素进行排序
*/
public static void sort(Comparable[] a){
//1.根据数组a的长度,确定增长量h的初始值;
int h = 1;
while(h<a.length/2){
h=2*h+1;
}
//2.希尔排序
while(h>=1){
//排序
//2.1.找到待插入的元素
for (int i=h;i<a.length;i++){
//2.2把待插入的元素插入到有序数列中
for (int j=i;j>=h;j-=h){
//待插入的元素是a[j],比较a[j]和a[j-h]
if (greater(a[j-h],a[j])){
//交换元素
exch(a,j-h,j);
}else{
//待插入元素已经找到了合适的位置,结束循环;
break;
}
}
}
//减小h的值
h= h/2;
}
}
/*
比较v元素是否大于w元素
*/
private static boolean greater(Comparable v,Comparable w){
return v.compareTo(w)>0;
}
/*
数组元素i和j交换位置
*/
private static void exch(Comparable[] a,int i,int j){
Comparable temp;
temp = a[i];
a[i]=a[j];
a[j]=temp;
}
}
测试类
import java.util.Arrays;
public class ShellTest {
public static void main(String[] args) {
Integer[] a = {9,1,2,5,7,4,8,6,3,5};
Shell.sort(a);
System.out.println(Arrays.toString(a));//{1,2,3,4,5,5,6,7,8,9}
}
}
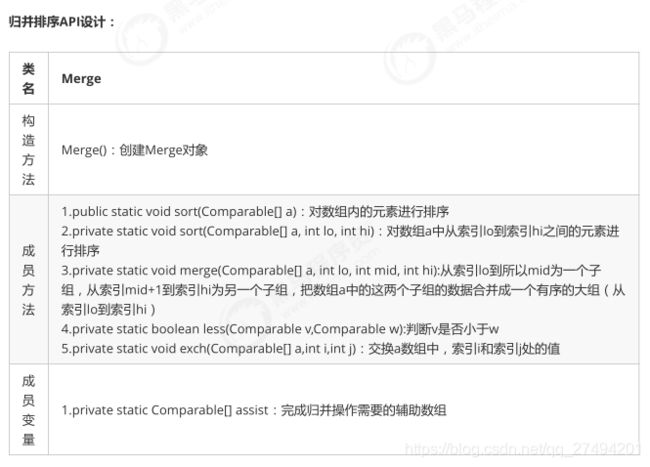
七丶归并排序
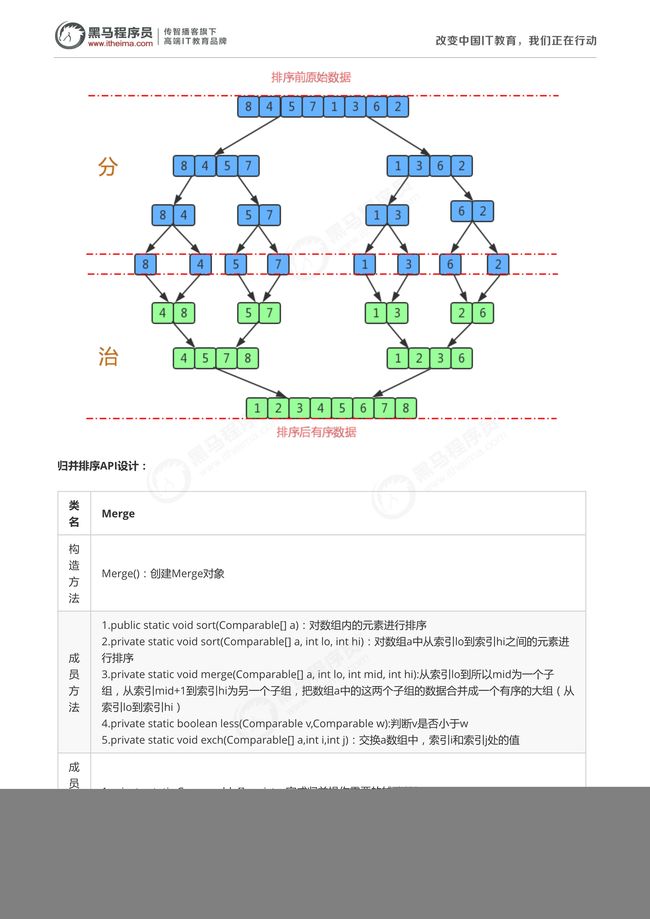
排序原理:
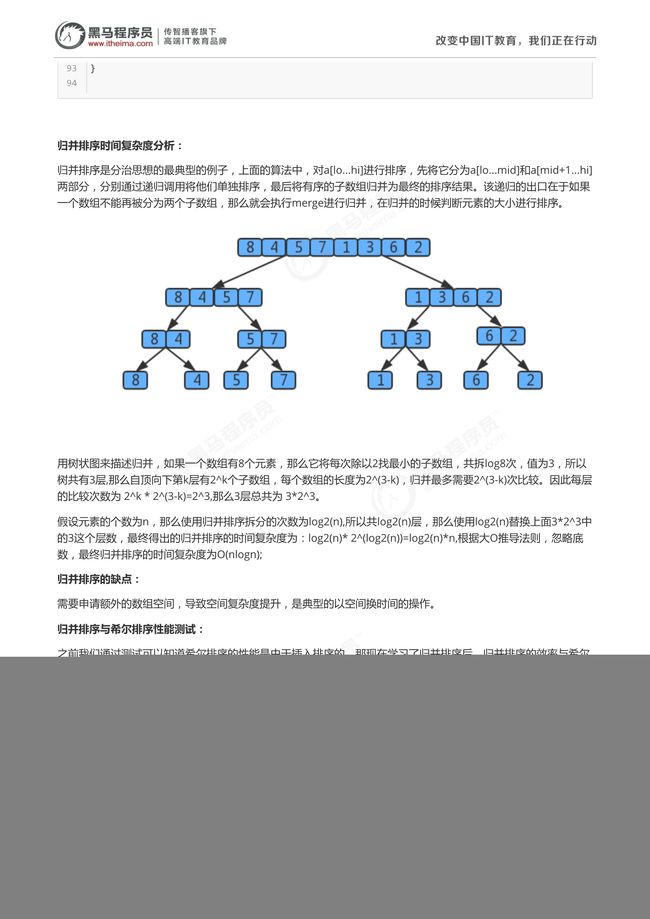
1.尽可能的一组数据拆分成两个元素相等的子组,并对每一个子组继续拆分,直到拆分后的每个子组的元素个数是
1为止。
2.将相邻的两个子组进行合并成一个有序的大组;
3.不断的重复步骤2,直到最终只有一个组为止。
public class Merge {
//归并所需要的辅助数组
private static Comparable[] assist;
/*
比较v元素是否小于w元素
*/
private static boolean less(Comparable v, Comparable w) {
return v.compareTo(w)<0;
}
/*
数组元素i和j交换位置
*/
private static void exch(Comparable[] a, int i, int j) {
Comparable t = a[i];
a[i] = a[j];
a[j] = t;
}
/*
对数组a中的元素进行排序
*/
public static void sort(Comparable[] a) {
//1.初始化辅助数组assist;
assist = new Comparable[a.length];
//2.定义一个lo变量,和hi变量,分别记录数组中最小的索引和最大的索引;
int lo=0;
int hi=a.length-1;
//3.调用sort重载方法完成数组a中,从索引lo到索引hi的元素的排序
sort(a,lo,hi);
}
/*
对数组a中从lo到hi的元素进行排序
*/
private static void sort(Comparable[] a, int lo, int hi) {
//做安全性校验;
if (hi<=lo){
return;
}
//对lo到hi之间的数据进行分为两个组
int mid = lo+(hi-lo)/2;// 5,9 mid=7
//分别对每一组数据进行排序
sort(a,lo,mid);
sort(a,mid+1,hi);
//再把两个组中的数据进行归并
merge(a,lo,mid,hi);
}
/*
对数组中,从lo到mid为一组,从mid+1到hi为一组,对这两组数据进行归并
*/
private static void merge(Comparable[] a, int lo, int mid, int hi) {
//定义三个指针
int i=lo;
int p1=lo;
int p2=mid+1;
//遍历,移动p1指针和p2指针,比较对应索引处的值,找出小的那个,放到辅助数组的对应索引处
while(p1<=mid && p2<=hi){
//比较对应索引处的值
if (less(a[p1],a[p2])){
assist[i++] = a[p1++];
}else{
assist[i++]=a[p2++];
}
}
//遍历,如果p1的指针没有走完,那么顺序移动p1指针,把对应的元素放到辅助数组的对应索引处
while(p1<=mid){
assist[i++]=a[p1++];
}
//遍历,如果p2的指针没有走完,那么顺序移动p2指针,把对应的元素放到辅助数组的对应索引处
while(p2<=hi){
assist[i++]=a[p2++];
}
//把辅助数组中的元素拷贝到原数组中
for(int index=lo;index<=hi;index++){
a[index]=assist[index];
}
}
}
测试类
import java.util.Arrays;
public class MergeTest {
public static void main(String[] args) {
Integer[] a = {8,4,5,7,1,3,6,2};
Merge.sort(a);
System.out.println(Arrays.toString(a));//{1,2,3,4,5,6,7,8}
}
}
八丶快速排序
排序原理:
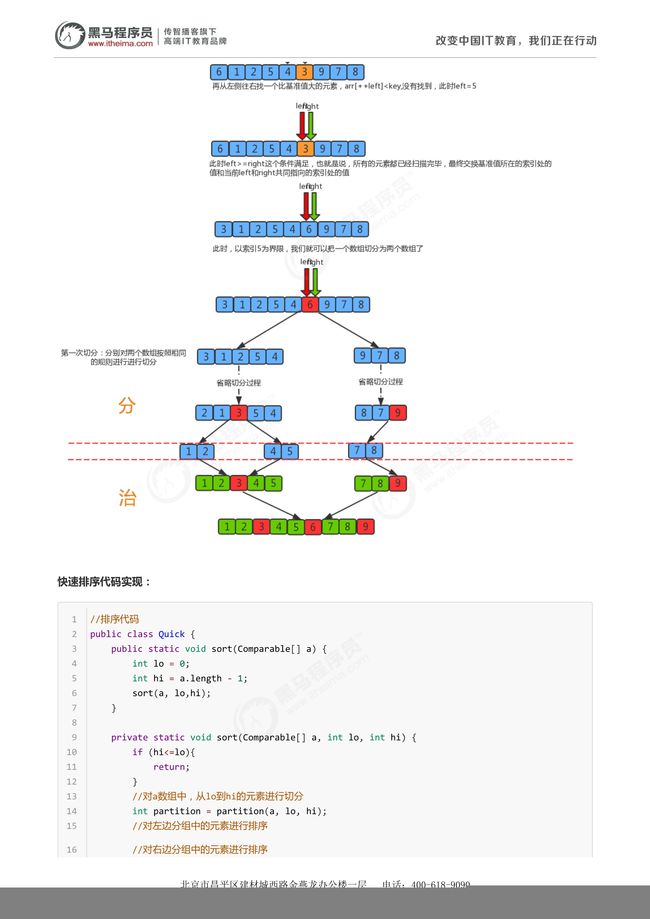
1.首先设定一个分界值,通过该分界值将数组分成左右两部分;
2.将大于或等于分界值的数据放到到数组右边,小于分界值的数据放到数组的左边。此时左边部分中各元素都小于
或等于分界值,而右边部分中各元素都大于或等于分界值;
切分原理:
把一个数组切分成两个子数组的基本思想:
1.找一个基准值,用两个指针分别指向数组的头部和尾部;
2.先从尾部向头部开始搜索一个比基准值小的元素,搜索到即停止,并记录指针的位置;
3.再从头部向尾部开始搜索一个比基准值大的元素,搜索到即停止,并记录指针的位置;
4.交换当前左边指针位置和右边指针位置的元素;
5.重复2,3,4步骤,直到左边指针的值大于右边指针的值停止。
package cn.itcast.algorithm.sort;
public class Quick {
/*
比较v元素是否小于w元素
*/
private static boolean less(Comparable v, Comparable w) {
return v.compareTo(w) < 0;
}
/*
数组元素i和j交换位置
*/
private static void exch(Comparable[] a, int i, int j) {
Comparable t = a[i];
a[i] = a[j];
a[j] = t;
}
//对数组内的元素进行排序
public static void sort(Comparable[] a) {
int lo = 0;
int hi = a.length-1;
sort(a,lo,hi);
}
//对数组a中从索引lo到索引hi之间的元素进行排序
private static void sort(Comparable[] a, int lo, int hi) {
//安全性校验
if (hi<=lo){
return;
}
//需要对数组中lo索引到hi索引处的元素进行分组(左子组和右子组);
int partition = partition(a, lo, hi);//返回的是分组的分界值所在的索引,分界值位置变换后的索引
//让左子组有序
sort(a,lo,partition-1);
//让右子组有序
sort(a,partition+1,hi);
}
//对数组a中,从索引 lo到索引 hi之间的元素进行分组,并返回分组界限对应的索引
public static int partition(Comparable[] a, int lo, int hi) {
//确定分界值
Comparable key = a[lo];
//定义两个指针,分别指向待切分元素的最小索引处和最大索引处的下一个位置
int left=lo;
int right=hi+1;
//切分
while(true){
//先从右往左扫描,移动right指针,找到一个比分界值小的元素,停止
while(less(key,a[--right])){
if (right==lo){
break;
}
}
//再从左往右扫描,移动left指针,找到一个比分界值大的元素,停止
while(less(a[++left],key)){
if (left==hi){
break;
}
}
//判断 left>=right,如果是,则证明元素扫描完毕,结束循环,如果不是,则交换元素即可
if (left>=right){
break;
}else{
exch(a,left,right);
}
}
//交换分界值
exch(a,lo,right);
return right;
}
}
测试类
import java.util.Arrays;
public class QuickTest {
public static void main(String[] args) {
Integer[] a= {6, 1, 2, 7, 9, 3, 4, 5, 8};
Quick.sort(a);
System.out.println(Arrays.toString(a));//{1, 2, 3, 4, 5, 6, 7, 8, 9}
}
}
九丶排序的稳定性
1、稳定性的定义:
数组arr中有若干元素,其中A元素和B元素相等,并且A元素在B元素前面,如果使用某种排序算法排序后,能够保
证A元素依然在B元素的前面,可以说这个该算法是稳定的。
2、稳定性的意义:
如果一组数据只需要一次排序,则稳定性一般是没有意义的,如果一组数据需要多次排序,稳定性是有意义的。例
如要排序的内容是一组商品对象,第一次排序按照价格由低到高排序,第二次排序按照销量由高到低排序,如果第
二次排序使用稳定性算法,就可以使得相同销量的对象依旧保持着价格高低的顺序展现,只有销量不同的对象才需
要重新排序。这样既可以保持第一次排序的原有意义,而且可以减少系统开销。
十丶测试各大排序法的时间消耗
package shujujiegou.rui.test;
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.ArrayList;
import shujujiegou.rui.sort.Bubble;
import shujujiegou.rui.sort.Merge;
import shujujiegou.rui.sort.Quick;
import shujujiegou.rui.sort.Selection;
import shujujiegou.rui.sort.Shell;
import shujujiegou.rui.sort.insertion;
/*
* 测试【希尔、插入、归并排序的时间消耗】
*/
public class SortCompare {
//调用不同的测试方法,完成测试
public static void main(String[] args) throws Exception {
//1.创建一个ArrayList集合,保存读取出来的整数
ArrayList<Integer> list = new ArrayList<>();
//2.创建缓存读取流BuffereReader,读取数据,并存储到ArrayList中
BufferedReader reader = new BufferedReader(new InputStreamReader(SortCompare.class.getClassLoader().getResourceAsStream("reverse_arr.txt")));
String line = null;
while((line=reader.readLine())!=null) {
//line是字符串,把line转换成Integer,存到集合中
int i = Integer.parseInt(line);
list.add(i);
}
reader.close();//关闭流
//3.把ArrayList集合转换成数组
Integer[] a = new Integer[list.size()];
list.toArray(a);
//4.调用测试代码完成测试
// testInsertion(a); // 插入排序 - 24177毫秒
// testShell(a); // 希尔排序 - 28毫秒
// testMerge(a); // 归并排序 - 60毫秒
// testBubble(a); // 冒泡排序 - 24031毫秒
// testSelection(a); // 选择排序 - 14894毫秒
// testQuick(a); // 快速排序
}
//测试冒泡排序法
public static void testBubble(Integer[] a) {
//1.获取执行之前的时间
long start = System.currentTimeMillis();
//2.执行算法代码
Bubble.sort(a);
//3.获取执行之后的时间
long end = System.currentTimeMillis();
//4.算出程序执行时间并输出
System.out.println("冒泡排序执行的时间为:"+(end-start)+"毫秒");
}
//测试选择排序法
public static void testSelection(Integer[] a) {
//1.获取执行之前的时间
long start = System.currentTimeMillis();
//2.执行算法代码
Selection.sort(a);
//3.获取执行之后的时间
long end = System.currentTimeMillis();
//4.算出程序执行时间并输出
System.out.println("选择排序执行的时间为:"+(end-start)+"毫秒");
}
//测试快速排序法
public static void testQuick(Integer[] a) {
//1.获取执行之前的时间
long start = System.currentTimeMillis();
//2.执行算法代码
Quick.sort(a);
//3.获取执行之后的时间
long end = System.currentTimeMillis();
//4.算出程序执行时间并输出
System.out.println("快速排序执行的时间为:"+(end-start)+"毫秒");
}
//测试希尔排序
public static void testShell(Integer[] a) {
//1.获取执行之前的时间
long start = System.currentTimeMillis();
//2.执行算法代码
Shell.sort(a);
//3.获取执行之后的时间
long end = System.currentTimeMillis();
//4.算出程序执行时间并输出
System.out.println("希尔排序执行的时间为:"+(end-start)+"毫秒");
}
//测试插入排序
public static void testInsertion(Integer[] a) {
//1.获取执行之前的时间
long start = System.currentTimeMillis();
//2.执行算法代码
insertion.sort(a);
//3.获取执行之后的时间
long end = System.currentTimeMillis();
//4.算出执行的时间并输出
System.out.println("插入排序执行时间为:"+(end-start)+"毫秒");
}
//测试归并排序
public static void testMerge(Integer[] a) {
//1.获取执行之前的时间
long start = System.currentTimeMillis();
//2.执行算法代码
Merge.sort(a);
//3.获取执行之后的时间
long end = System.currentTimeMillis();
//4.算出程序执行的时间并输出
System.out.println("归并排序执行的时间为:"+(end-start)+"毫秒");
}
}