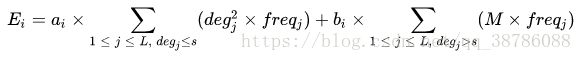牛客网练习赛15 C、吉姆的奇思妙想（数学单调性 + 二分法）

题目链接

题意： 给你正整数a、b，求出s取某个整数时，Ei的最小值。（各参数的范围相当复杂）

Ei=ai×∑1≤j≤L,degj≤s(deg2j×freqj)+bi×∑1≤j≤L,degj>s(M×freqj)=∑1≤j≤L,degj≤s(ai×deg2j×freqj−bi×M×freqj)+bi×M×∑1≤j≤Lfreqj=∑1≤j≤L,degj≤s(ai×deg2j−bi×M)×freqj+bi×M×∑1≤j≤Lfreqjbi×M×∑1≤j≤Lfreqj,这是一个常量，无论s取什么值，它都不变。因为a为正整数，那么(ai×deg2j−bi×M)随j增大，deg2j增大，所以我们仅需要将所有(ai×deg2j−bi×M)小于0的项找出，（为正值就开始加了）即找出最大的j满足即可(54)(55)(56)(57)(58)(59)(60) (54) E i = a i × ∑ 1 ≤ j ≤ L , d e g j ≤ s ( d e g j 2 × f r e q j ) + b i × ∑ 1 ≤ j ≤ L , d e g j > s ( M × f r e q j ) (55) = ∑ 1 ≤ j ≤ L , d e g j ≤ s ( a i × d e g j 2 × f r e q j − b i × M × f r e q j ) + b i × M × ∑ 1 ≤ j ≤ L f r e q j (56) = ∑ 1 ≤ j ≤ L , d e g j ≤ s ( a i × d e g j 2 − b i × M ) × f r e q j + b i × M × ∑ 1 ≤ j ≤ L f r e q j (57) (58) b i × M × ∑ 1 ≤ j ≤ L f r e q j , 这 是 一 个 常 量 ， 无 论 s 取 什 么 值 ， 它 都 不 变 。 (59) 因 为 a 为 正 整 数 ， 那 么 ( a i × d e g j 2 − b i × M ) 随 j 增 大 ， d e g j 2 增 大 ， 所 以 我 们 仅 需 要 将 (60) 所 有 ( a i × d e g j 2 − b i × M ) 小 于 0 的 项 找 出 ， （ 为 正 值 就 开 始 加 了 ） 即 找 出 最 大 的 j 满 足 即 可

解法：已经很明显了，预处理求出所有前i个deg²*freq的和、前i个freq的和。
     二分找出最大j的取值t，使得（a*deg[j]²*M）,然后答案就能以O(1)立刻求出。
     记住不能按推导公式直接求解： 因为b*M*sum_freq[L]超了LTM，只能求代入原公式
     求出b*M*（sum_freq[L]-sum_freq[t]）.

     二分也可用upper_bound()代替。

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#define llt unsigned long long int
using namespace std;

const int Size=2*1e5+7;
llt d[Size],f[201000],Sd[201000],Sf[201000];

llt M,L;
int binfen(llt x,llt a){
    if(a*d[1]>x) return -1;
    int l=1,r=L;
    while(lint mid=(l+r+1)>>1;
        if(a*d[mid]else r=mid-1;
    }

    return l;
}
int main(){

    scanf("%llu%llu",&M,&L);
    llt a,b;
    Sd[0]=Sf[0]=0;
    for(int i=1;i<=L;++i){
        scanf("%llu%llu",&a,&f[i]);
        d[i]=a*a;
        Sd[i]=Sd[i-1]+d[i]*f[i];
        Sf[i]=Sf[i-1]+f[i];
    }

    int Q;
    scanf("%d",&Q);
    while(Q--){
        llt a,b;
        scanf("%llu%llu",&a,&b);
        //cout<
        int t=binfen(b*M,a);
        if(t==-1)printf("%llu\n",b*M*(Sf[L]));
        else printf("%llu\n",a*(Sd[t])+b*M*(Sf[L]-Sf[t]));
    }

    return 0;
}