A-Softmax(SphereFace)

论文：SphereFace：https://arxiv.org/abs/1704.08063

SphereFace在MegaFace数据集上识别率在2017年排名第一，用的A-Softmax Loss有着清晰的几何定义，能在比较小的数据集上达到不错的效果。

首先，需要先科普一下在训练和测试人脸识别分类器的时候经常被提到的Open-set 和Close-set。Figure 1是一个直观的展示。

close-set，就是所有的测试集都在训练集中出现过。所以预测结果是图片的ID，如果想要测试两张图片是否是同一个，那么就看这两张图片的预测ID是否一样即可。

open-set，就是测试的图片并没有在训练集中出现过，那么每张测试图片的预测结果是特征向量，如果想要比较两张图片的人脸是否属于同一个人，需要测试图像特征向量的距离。

然而softmax loss仅仅能够使得特征可分，还不能够使得特征具有可判别性。尽管有一些方法通过结合softmax loss和 contrastive loss，center loss去提高特征的可判别性，但是contrastive loss和center loss需要精心地构建图像对和三元组，不仅耗时而且构建的训练对会对识别性能影响很大。因此，在这篇论文中，作者提出了angular softmax（A-Softmax）loss。

一步一步推导A-Softmax

modified Softmax

为了让特征学习到更可分的角度特性，作者首先对Softmax进行了一些改进：

为了简单起见，先假设是一个二分类问题，

softmax的决策边界是：

如果我们通过W的归一化来添加约束条件：


那么我们可以得到决策边界：

这样的损失函数称为改进了的Softmax（modified Softmax）,通过这样的损失函数学习，可以使得学习到的特征具有更明显的角分布，因为决策边界只与角有关。

假设对于输入特征Xi，它的标签是Yi，用f(Yi)表示WiXi即Softmax对应Yi那一位的输出

Softmax的损失函数：

modified Softmax的损失函数：

A-Softmax

还可以进一步修改

通过添加系数m，对θ1有了更强的约束，因为cos(mθ1)比cosθ1要小。此时损失函数变为：

由于cosθ在[0,pi]上单调递减，因此θ有上界：

我们为了使得这个函数随角度单调递减，构造一个函数去代替cos：

A-Softmax的性质

**性质：**在二分类问题中，对于一个训练好的A-Softmax层，两个类的类内角度特征距离为m−1m+1θ
其中θ表示两个类的权值W1，W2之间的夹角。证明：

性质一：
A-Softmax Loss定义了一个大角度间隔的学习方法，m越大这个间隔的角度也就越大，相应区域流形的大小就越小，这就导致了训练的任务也越困难。

定义：定义mmin为当m>mmin时,类内的最大角度特征距离小于类间的最小角度特征距离。

性质二：

加粗样式

几种损失函数

softmax损失仅仅能够学到分辨性不够强的特征，除此之外，还有contrastive loss，center loss，triplet loss。

但是它们都在一定程度上存在弊端：

center loss仅能使得类内紧凑，无法使得类间可分。

contrastive loss和triplet loss需要pair/triplet 挖掘过程，增加时间的损耗。

除此之外，还有一个更关键之处：以上的损失函数都使用了欧式距离，而softmax损失学习到的特征有角度上的分布特性。

2. A-Softmax Loss的性质

性质1：
A-Softmax Loss定义了一个大角度间隔的学习方法，m越大这个间隔的角度也就越大，相应区域流形的大小就越小，这就导致了训练的任务也越困难。
这个性质是相当容易理解的，如图1所示：这个间隔的角度为(m−1)θ1，所以m越大，则间隔的角度就越小；同时mθ1<π，当所以m越大，则相应的区域流形θ1就越小。

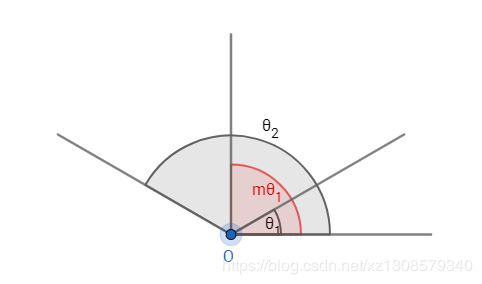
定义1：mmin被定义为当m>mmin时有类内间的最大角度特征距离小于类间的最小角度特征距离。

实验及结果

训练集：CASIA-webface

batchsize： 128

28K次迭代收敛

测试时的算法：连接一张图以及其水平翻转的图的FC1输出，PCA降维后计算余弦距离

不同m对准确率的影响：

LFW得分：