堆排序——对简单选择排序的优化

1. 堆排序概述

• 堆排序 Heap Sort是对简单选择排序的优化：选择排序是在待排序的$i$个中选择最小（或最大）的数，交换到数组前面来，每次都需要比较$i-1$次，如果在确保每次都能够选择最小（或最大）数的同时，对每次比较结果进行调整，那么排序的效率会有更大的提升，堆排序正是做这样的事情。
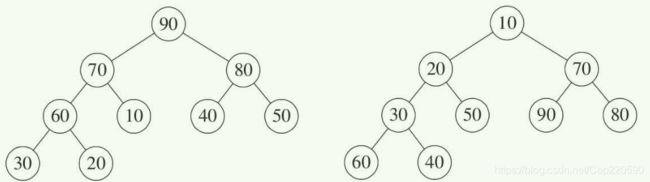
• 堆排序算法是Floyd和Williams在1964年共同发明的，同时，他们发明了“堆”这样的数据结构：
  • 堆：堆是某一节点都小于（或都大于）左右子树的完全二叉树。
  • 堆排序的最坏、最好、平均时间复杂度均为$O(nlogn)$，也是不稳定排序
  • 堆的分类
    • 大顶堆：节点大于左右子树
    • 小顶堆：节点小于左右子树
      

如果按照层序遍历的方式给节点从1开始编号，则节点之间满足如下关系：

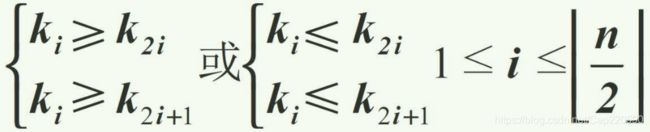
如果堆是数组顺序存储的：

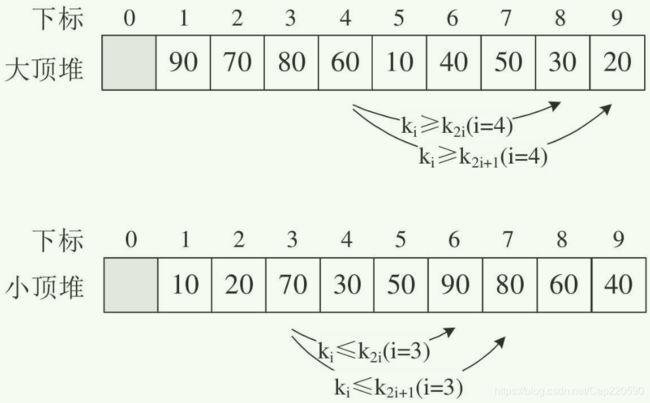
2. 堆排序思想

• 堆排序的基本思想如下（以升序为例）：
  • 步骤一：将待排序的数组构造成一个大顶堆，此时数组的最大值就是大顶堆的根节点
  • 步骤二：将根节点和末尾元素进行交换，此时末尾元素就是最大值
  • 步骤三：去掉此末尾元素（已排序好），将$n-1$个元素重新按步骤一排序
  • 按以上如此反复执行，就能够得到升序的数组了

3. 图解堆排序

假设有一个数组$\{4,6,8,5,9\}$，要求使用堆排序法，将数组升序排序
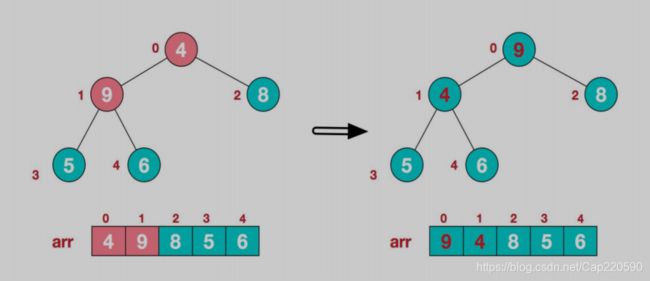
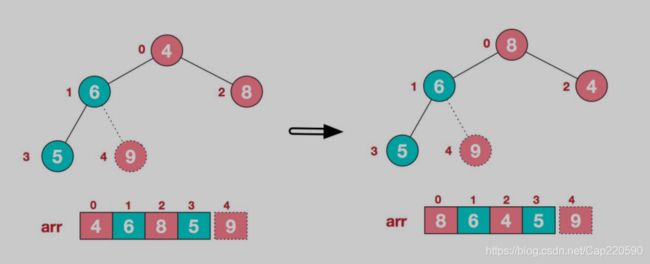
步骤一：构造初始堆，按要求将给定无序数组构造成一个大顶堆。

1. 初始无序数组结构如下：
   
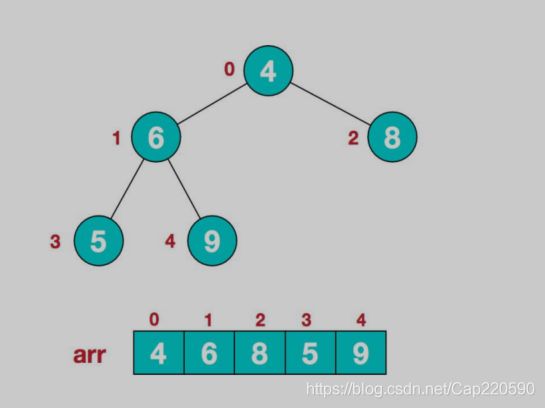
2. 此时我们从最后一个非叶子节点开始（我们的目标是大顶堆的根节点，非叶子节点自然不用调整），最后一个非叶子节点的计算公式是$\frac{arr.length}{2}-1$，我们从左至右，从下至上进行调整。

堆是一颗完全二叉树，设某堆总共有n个节点，则最后一个非叶子节点的计算公式如下：
$$\frac{n}{2}-1$$
公式的推导推荐博客：堆排序（完全二叉树）最后一个非叶子节点的序号是n/2-1的原因

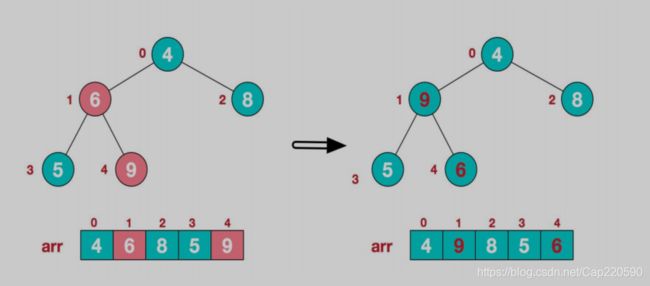
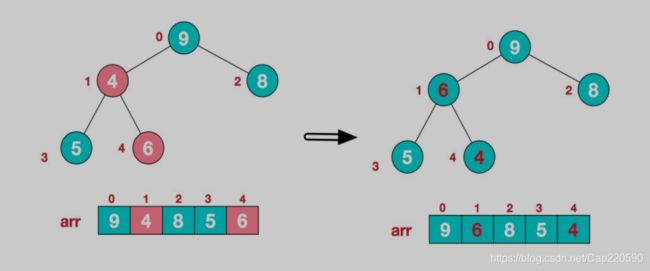
这里我们找到最后一个叶子节点是6，根据大顶堆的定义最其进行调整——在子树[6,5,9]中找到最大的值9，9和6互换，这样就形成一个局部大顶堆了。

3. 找到第二个非叶子节点4，由于[4, 9, 8]中9元素最大，4和9互换。
   
4. 这时，交换导致了子树[4, 5, 6]结构混乱，继续调整，[4, 5, 6]中6最大，交换4和6
   

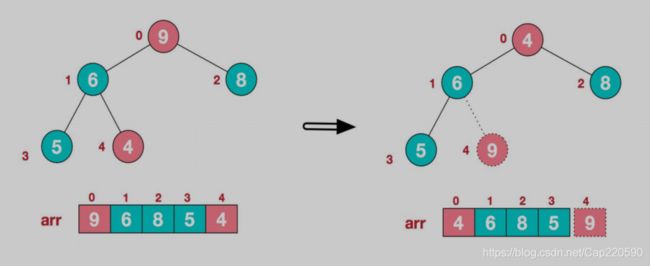
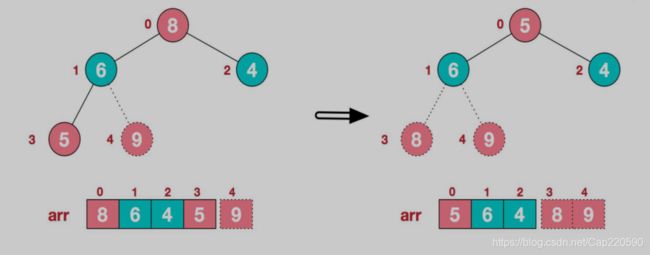
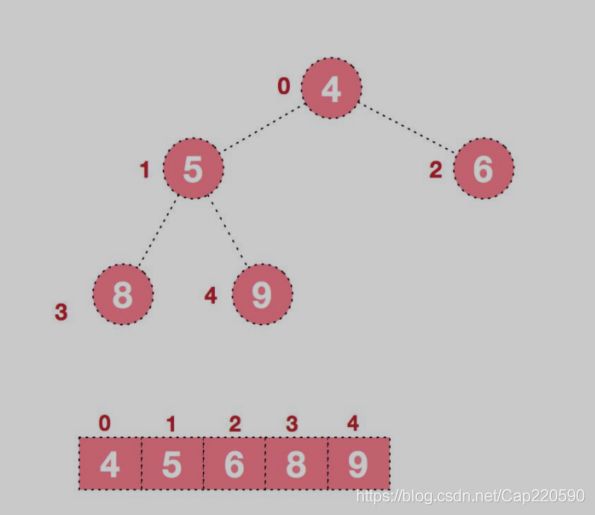
步骤二：将堆顶元素与末尾元素交换，然后继续重复步骤一

1. 将对顶元素9和末尾元素4交换
   

2. 重新调整结构，使其满足堆定义
   

3. 再将对顶元素8与末尾元素5进行交换，得到第二大元素8
   

4. 如此反复，最终我们得到一个有序的数组
   

4. 代码演示

堆排序最关键的代码是调整某一子树的成为大（小）顶堆（这一部对应上一节的步骤一，是一个难点来着，如果有看不懂的，可以在你IDE上开Debug查看调整过程）我们来看一下其代码：

    /**
     * 
某一子树调整为大顶堆
     * @param heapArray 需要进行调整的数组
     * @param noLeafIndex 非叶子节点的下标
     * @param range 需要进行调整的数组的范围
     */
    private static void maxHeapAdjust(int[] heapArray, int noLeafIndex, int range) {
        // 这里我们需要使用到循环
        // 因为对于某一子树的调整会导致原先调整好的下一层子树失调
        // 最终的目的是要将该父节点放到它应该放置的位置
        for(int maxChildNodeIndex = (noLeafIndex << 1) + 1; maxChildNodeIndex <= range; maxChildNodeIndex = (maxChildNodeIndex << 1) + 1){
            // maxChildNodeIndex默认是左子节点，如果右子节点也存在
            // 那么判断左右子节点哪个大，取最大子节点来操作
            if (maxChildNodeIndex + 1 <= range && heapArray[maxChildNodeIndex] < heapArray[maxChildNodeIndex+1] ){
                maxChildNodeIndex++;
            }
            // 比较父节点和最大子节点
            if(heapArray[noLeafIndex] < heapArray[maxChildNodeIndex]){
                // 父节点小于最大子节点
                // 那就交换父节点和最大子节点
                int temp = heapArray[noLeafIndex];
                heapArray[noLeafIndex] = heapArray[maxChildNodeIndex];
                heapArray[maxChildNodeIndex] = temp;
                // 将子节点的下标赋给父节点的下标
                noLeafIndex = maxChildNodeIndex;
            } else{
                break;
            }
        }
    }
    /**
     * 
某一子树调整为小顶堆
     * @param heapArray 需要进行调整的数组
     * @param noLeafIndex 非叶子节点的下标
     * @param range 需要进行调整的数组的范围
     */
    private static void minHeapAdjust(int[] heapArray, int noLeafIndex, int range) {
        // 这里我们需要使用到循环
        // 因为对于某一子树的调整会导致原先调整好的下一层子树失调
        // 最终的目的是要将该父节点放到它应该放置的位置
        for(int minChildNodeIndex = (noLeafIndex << 1) + 1; minChildNodeIndex <= range; minChildNodeIndex = (minChildNodeIndex << 1) + 1){
            // maxChildNodeIndex默认是左子节点，如果右子节点也存在
            // 那么判断左右子节点哪个大，取最小子节点来操作
            if (minChildNodeIndex + 1 <= range && heapArray[minChildNodeIndex] > heapArray[minChildNodeIndex+1] ){
                minChildNodeIndex++;
            }
            // 比较父节点和最大子节点
            if(heapArray[noLeafIndex] > heapArray[minChildNodeIndex]){
                // 父节点大于最大子节点
                // 那就交换父节点和最大子节点
                int temp = heapArray[noLeafIndex];
                heapArray[noLeafIndex] = heapArray[minChildNodeIndex];
                heapArray[minChildNodeIndex] = temp;
                // 将子节点的下标赋给父节点的下标
                noLeafIndex = minChildNodeIndex;
            } else{
                break;
            }
        }
    }

接下来我们来看一下完整代码：

package com.cap.heap;

/**
 * @author cap
 * @create 2020.08.08.15:18
 */
public class HeapSort {

    /**
     * 
堆排序算法——升序排序
     * @param heapArray 需要去排序的数组
     */
    public static void heapSort(int[] heapArray){
        heapSort(heapArray,false);
    }

    /**
     * 
堆排序算法
     * @param heapArray 需要去排序的数组
     * @param decreaseSort 如果为true则进行降序排序，为false为升序排序
     */
    public static void heapSort(int[] heapArray, boolean decreaseSort){

        // 从下往上调整：即从最后一个的非叶子节点开始
        for (int noLeafIndex = (heapArray.length >> 1) - 1; noLeafIndex >= 0; noLeafIndex--) {
            if (!decreaseSort) {
                maxHeapAdjust(heapArray, noLeafIndex, heapArray.length - 1);
            } else {
                minHeapAdjust(heapArray, noLeafIndex, heapArray.length - 1);
            }
        }

        for(int range = heapArray.length - 1; range > 0; range --){
            // 由大（小）顶堆定义可知，此时堆顶元素一定是最大（小）值
            // 将堆顶元素和末尾元素交换
            int temp = heapArray[0];
            heapArray[0] = heapArray[range];
            heapArray[range] = temp;
            // 原先大（小）顶堆已经调整好，现在只需要调整交换过的堆顶元素即可
            if(!decreaseSort){
                maxHeapAdjust(heapArray,0,range - 1);
            } else {
                minHeapAdjust(heapArray,0,range - 1);
            }
        }

    }

    /**
     * 
某一子树调整为大顶堆
     * @param heapArray 需要进行调整的数组
     * @param noLeafIndex 非叶子节点的下标
     * @param range 需要进行调整的数组的范围
     */
    private static void maxHeapAdjust(int[] heapArray, int noLeafIndex, int range) {
        // 这里我们需要使用到循环
        // 因为对于某一子树的调整会导致原先调整好的下一层子树失调
        // 最终的目的是要将该父节点放到它应该放置的位置
        for(int maxChildNodeIndex = (noLeafIndex << 1) + 1; maxChildNodeIndex <= range; maxChildNodeIndex = (maxChildNodeIndex << 1) + 1){
            // maxChildNodeIndex默认是左子节点，如果右子节点也存在
            // 那么判断左右子节点哪个大，取最大子节点来操作
            if (maxChildNodeIndex + 1 <= range && heapArray[maxChildNodeIndex] < heapArray[maxChildNodeIndex+1] ){
                maxChildNodeIndex++;
            }
            // 比较父节点和最大子节点
            if(heapArray[noLeafIndex] < heapArray[maxChildNodeIndex]){
                // 父节点小于最大子节点
                // 那就交换父节点和最大子节点
                int temp = heapArray[noLeafIndex];
                heapArray[noLeafIndex] = heapArray[maxChildNodeIndex];
                heapArray[maxChildNodeIndex] = temp;
                // 将子节点的下标赋给父节点的下标
                noLeafIndex = maxChildNodeIndex;
            } else{
                break;
            }
        }
    }
    /**
     * 
某一子树调整为小顶堆
     * @param heapArray 需要进行调整的数组
     * @param noLeafIndex 非叶子节点的下标
     * @param range 需要进行调整的数组的范围
     */
    private static void minHeapAdjust(int[] heapArray, int noLeafIndex, int range) {
        // 这里我们需要使用到循环
        // 因为对于某一子树的调整会导致原先调整好的下一层子树失调
        // 最终的目的是要将该父节点放到它应该放置的位置
        for(int minChildNodeIndex = (noLeafIndex << 1) + 1; minChildNodeIndex <= range; minChildNodeIndex = (minChildNodeIndex << 1) + 1){
            // maxChildNodeIndex默认是左子节点，如果右子节点也存在
            // 那么判断左右子节点哪个大，取最小子节点来操作
            if (minChildNodeIndex + 1 <= range && heapArray[minChildNodeIndex] > heapArray[minChildNodeIndex+1] ){
                minChildNodeIndex++;
            }
            // 比较父节点和最大子节点
            if(heapArray[noLeafIndex] > heapArray[minChildNodeIndex]){
                // 父节点大于最大子节点
                // 那就交换父节点和最大子节点
                int temp = heapArray[noLeafIndex];
                heapArray[noLeafIndex] = heapArray[minChildNodeIndex];
                heapArray[minChildNodeIndex] = temp;
                // 将子节点的下标赋给父节点的下标
                noLeafIndex = minChildNodeIndex;
            } else{
                break;
            }
        }
    }
}

测试一下：

    @Test
    public void tester(){
        int num = 8*100*10000;
        int[] arr = new int[num];
        for (int i = 0; i < num; i++) {
            arr[i] = (int)(Math.random() * num);
        }
        long start = System.currentTimeMillis();
        heapSort(arr);
        long end = System.currentTimeMillis();
        System.out.println("一共"+num+"个数据，耗时"+(end-start)+"毫秒");
    }

一共8000000个数据，耗时3352毫秒

测试下来，八百万个数据也就2~4秒，非常快

参考

1. 《大话数据结构》
2. 尚硅谷-韩顺平数据结构与算法（B站可搜索）