Python 图像处理 OpenCV (13): Scharr 算子和 LOG 算子边缘检测技术
![]()
前文传送门:
「Python 图像处理 OpenCV (1):入门」
「Python 图像处理 OpenCV (2):像素处理与 Numpy 操作以及 Matplotlib 显示图像」
「Python 图像处理 OpenCV (3):图像属性、图像感兴趣 ROI 区域及通道处理」
「Python 图像处理 OpenCV (4):图像算数运算以及修改颜色空间」
「Python 图像处理 OpenCV (5):图像的几何变换」
「Python 图像处理 OpenCV (6):图像的阈值处理」
「Python 图像处理 OpenCV (7):图像平滑(滤波)处理」
「Python 图像处理 OpenCV (8):图像腐蚀与图像膨胀」
「Python 图像处理 OpenCV (9):图像处理形态学开运算、闭运算以及梯度运算」
「Python 图像处理 OpenCV (10):图像处理形态学之顶帽运算与黑帽运算」
「Python 图像处理 OpenCV (11):Canny 算子边缘检测技术」
「Python 图像处理 OpenCV (12): Roberts 算子、 Prewitt 算子、 Sobel 算子和 Laplacian 算子边缘检测技术」
Scharr 算子
在说 Scharr 算子之前,必须要提的是前面我们介绍过的 Sobel 算子, Sobel 算子虽然可以有效的提取图像边缘,但是对图像中较弱的边缘提取效果较差。
这是由于 Sobel 算子在计算相对较小的核的时候,其近似计算导数的精度比较低,例如一个 3 * 3 的 Sobel 算子,在梯度角度接近水平或垂直方向时,其不精确性就非常明显。
因此引入 Scharr 算子。 Scharr 算子是对 Sobel 算子差异性的增强,两者之间的在检测图像边缘的原理和使用方式上相同。
而 Scharr 算子的主要思路是通过将模版中的权重系数放大来增大像素值间的差异。
Scharr 算子又称为 Scharr 滤波器,也是计算 x 或 y 方向上的图像差分,在 OpenCV 中主要是配合 Sobel 算子的运算而存在的,其滤波器的滤波系数如下:
G x = [ − 3 0 3 − 10 0 10 − 3 0 3 ] Gx = \left[ \begin{matrix} -3 & 0 & 3\\ -10 & 0 & 10\\ -3 & 0 & 3\\ \end{matrix} \right] Gx=⎣⎡−3−10−30003103⎦⎤
G y = [ − 3 − 10 − 3 0 0 0 3 10 3 ] Gy = \left[ \begin{matrix} -3 & -10 & -3\\ 0 & 0 & 0\\ 3 & 10 & 3\\ \end{matrix} \right] Gy=⎣⎡−303−10010−303⎦⎤
Scharr 算子在 OpenCV 中的方法原型如下:
def Scharr(src, ddepth, dx, dy, dst=None, scale=None, delta=None, borderType=None):
- src: 表示输入图像
- ddepth: 表示目标图像所需的深度,针对不同的输入图像,输出目标图像有不同的深度
- dx: 表示 x 方向上的差分阶数,取值 1 或 0
- dy: 表示 y 方向上的差分阶数,取值 1 或 0
可以看到,函数 Scharr() 和 Sobel() 是非常的相似,在使用上也是完全一样的,下面看一个示例:
import cv2 as cv
import matplotlib.pyplot as plt
img = cv.imread("maliao.jpg")
rgb_img = cv.cvtColor(img, cv.COLOR_BGR2RGB)
gray_img = cv.cvtColor(img, cv.COLOR_BGR2GRAY)
# Scharr 算子
x = cv.Scharr(gray_img, cv.CV_16S, 1, 0) # X 方向
y = cv.Scharr(gray_img, cv.CV_16S, 0, 1) # Y 方向
absX = cv.convertScaleAbs(x)
absY = cv.convertScaleAbs(y)
Scharr = cv.addWeighted(absX, 0.5, absY, 0.5, 0)
# 显示图形
plt.rcParams['font.sans-serif']=['SimHei']
titles = ['原始图像', 'Scharr 算子']
images = [rgb_img, Scharr]
for i in range(2):
plt.subplot(1, 2, i + 1), plt.imshow(images[i], 'gray')
plt.title(titles[i])
plt.xticks([]), plt.yticks([])
plt.show()
LOG 算子
LOG ( Laplacian of Gaussian ) 边缘检测算子是 David Courtnay Marr 和 Ellen Hildreth 在 1980 年共同提出的,也称为 Marr & Hildreth 算子,它根据图像的信噪比来求检测边缘的最优滤波器。该算法首先对图像做高斯滤波,然后再求其拉普拉斯( Laplacian )二阶导数,根据二阶导数的过零点来检测图像的边界,即通过检测滤波结果的零交叉( Zero crossings )来获得图像或物体的边缘。
LOG 算子实际上是把 Gauss 滤波和 Laplacian 滤波结合了起来,先平滑掉噪声,再进行边缘检测。
LOG 算子与视觉生理中的数学模型相似,因此在图像处理领域中得到了广泛的应用。
它具有抗干扰能力强,边界定位精度高,边缘连续性好,能有效提取对比度弱的边界等特点。
常见的 LOG 算子是 5 * 5 的模板;
G y = [ − 2 − 4 − 4 − 4 − 2 − 4 0 8 0 − 4 − 4 8 24 8 − 4 − 4 0 8 0 − 4 − 2 − 4 − 4 − 4 − 2 ] Gy = \left[ \begin{matrix} -2 & -4 & -4 & -4 & -2\\ -4 & 0 & 8 & 0 & -4\\ -4 & 8 & 24 & 8 & -4\\ -4 & 0 & 8 & 0 & -4\\ -2 & -4 & -4 & -4 & -2\\ \end{matrix} \right] Gy=⎣⎢⎢⎢⎢⎡−2−4−4−4−2−4080−4−48248−4−4080−4−2−4−4−4−2⎦⎥⎥⎥⎥⎤
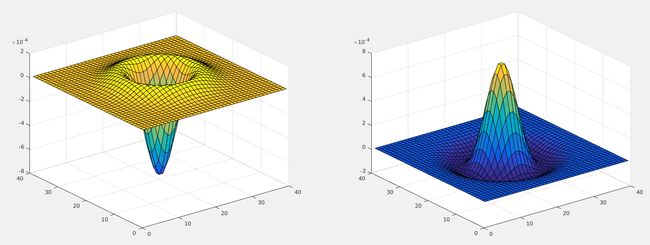
LOG 算子到中心的距离与位置加权系数的关系曲线像墨西哥草帽的剖面,所以 LOG 算子也叫墨西哥草帽滤波器。
示例代码如下:
import cv2 as cv
import matplotlib.pyplot as plt
# 读取图像
img = cv.imread("maliao.jpg")
rgb_img = cv.cvtColor(img, cv.COLOR_BGR2RGB)
gray_img = cv.cvtColor(img, cv.COLOR_BGR2GRAY)
# 先通过高斯滤波降噪
gaussian = cv.GaussianBlur(gray_img, (3, 3), 0)
# 再通过拉普拉斯算子做边缘检测
dst = cv.Laplacian(gaussian, cv.CV_16S, ksize=3)
LOG = cv.convertScaleAbs(dst)
# 用来正常显示中文标签
plt.rcParams['font.sans-serif'] = ['SimHei']
# 显示图形
titles = ['原始图像', 'LOG 算子']
images = [rgb_img, LOG]
for i in range(2):
plt.subplot(1, 2, i + 1), plt.imshow(images[i], 'gray')
plt.title(titles[i])
plt.xticks([]), plt.yticks([])
plt.show()
小结
边缘检测算法主要是基于图像强度的一阶和二阶导数,但导数通常对噪声很敏感,因此需要采用滤波器来过滤噪声,并调用图像增强或阈值化算法进行处理,最后再进行边缘检测。
参考
https://blog.csdn.net/Eastmount/article/details/89056240
https://blog.csdn.net/qq_42722197/article/details/103825409
https://www.jianshu.com/p/2ac784fd22fc