混合个人训练第四十六场（A,B题解） A 数论线代全家桶 (all） B: 看星星 (stars)

A 数论线代全家桶 (all)


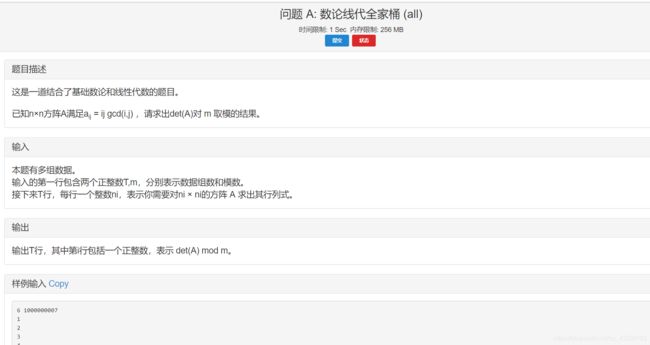
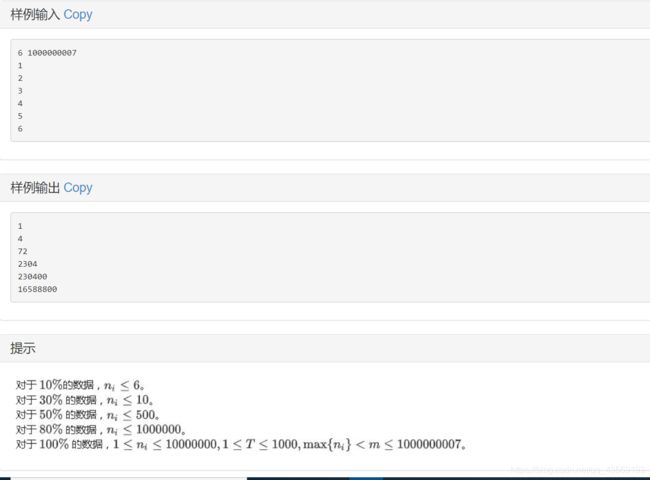
题意如图。
思路： 首先发现

1 = 1 * 1 * 1;								n=1;
4 = 1 * 4 * 1;								n=2;
72 = 4 * 18=4 * 9 * 2;						n=3;
2304 = 72 * 16 * 2;							n=4;
23040 = 2304 * 25 * 4;						n=5
16588800 = 23040 * 36 * 2;					n=6;

然后感觉有一种奇怪的规律:
令f[n]为该n阶方阵所需要的值，发现f[n]=f[n-1] * n^2 * x;
然后前6个x为 1 1 2 2 4 2；
这不就是欧拉函数？暴力跑到n=10，发现没有问题。
然后直接线性筛欧拉函数打表预处理一下，就行了。
代码：

#include
using namespace std;
const int N=1e7+1500;
typedef long long ll;
bool vis[N];
int prime[N];
ll phi[N],f[N];
ll cnt=0;
void Prime()
{
    int n=10000000;
    vis[1]=1;
    for(int i=2;i<=n;i++)
    {
        if(!vis[i])
        {
            prime[++cnt]=i;
            phi[i]=i-1;
        }
        for(int j=1;j<=cnt&&i*prime[j]<=n;j++)
        {
            vis[i*prime[j]]=1;
            phi[i*prime[j]]=phi[i]*phi[prime[j]];
            if(i%prime[j]==0)
            {
                phi[i*prime[j]]=phi[i]*prime[j];
                break;
            }
        }
    }
    //cout<
}
int main()
{
    Prime();
    ll t,mod;
    cin>>t>>mod;
    ll n=10000000;
    f[1]=1;
    for(ll i=2;i<=n;i++)
    {
        ll op=i*i;  op%=mod;
        f[i]=f[i-1]*op; f[i]%=mod;
        f[i]*=phi[i];   f[i]%=mod;
    }
    while(t--)
    {
        cin>>n;
        cout<<f[n]<<endl;
    }
    return 0;
}

B 看星星(stars)


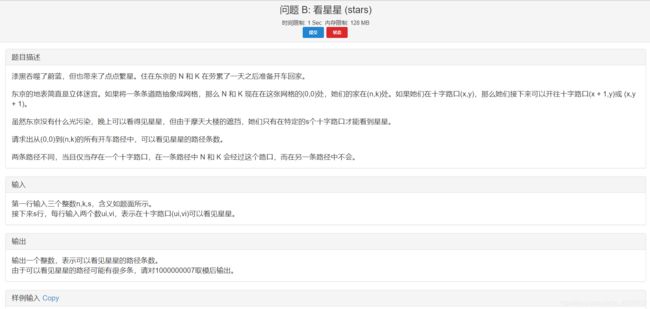
题意如图。
思路：组合数学加动态点更新。
首先要知道对于两个点a,b，他们之间是有先后关系的:

要么是从a能走到b,
要么是从b能走到a。
不可能出现a能走到b而且b能走到a的情况。

感觉相当于一个拓扑之类的。
所以前提条件先把哪几个坐标进行排序。
然后就可以dp了。
dp[i]代表从坐标(0,0)到坐标（x_i,y_i） 的路径数。
然后你又就可以求出来第i个点到终点的路径数，利用乘法法则加到总方案数上。
然后利用第i个点，尝试性更新dp[i+1]到dp[s]（为什么用尝试性，因为不一定能更新成功）。
如果第j个点可以被第i个点更新，dp[j]=dp[j]-dp[i]*cal(xj-xi+yj-yi,xj-xi);
然后就没了。
另外一个需要注意的点时，组合数打表要到2e6，因为cal 里面最大要计算n+k,所以要开双倍。
代码：

#include
using namespace std;
const int N=2e6+1500;
typedef long long ll;
struct node{
ll x,y;
}a[N];
ll mod=1e9+7;
ll f[N],dp[N];
bool cmp(node a,node b)
{
    if(a.x==b.x)
        return a.y<b.y;
    return a.x<b.x;
}
void Pre()
{
    ll n=2000100;
    f[0]=1;
    for(int i=1;i<=n;i++)
    {
        f[i]=f[i-1]*i;
        f[i]%=mod;
    }
}
ll qpow(ll a,ll b)
{
    ll s=1;
    while(b)
    {
        if(b&1)
        {
            s=(s*a)%mod;
        }
        a=(a*a)%mod;
        b/=2;
    }
    return s;
}
ll inv(ll x)
{
    return qpow(x,mod-2);
}
ll cal(ll n,ll m)
{
    ll op=f[n-m]*f[m];
    op%=mod;
    op=f[n]*inv(op);
    op%=mod;
    return op;
}
int main()
{
    ll n,m,k;
    Pre();
    cin>>n>>m>>k;
    for(int i=1;i<=k;i++)
    {
        cin>>a[i].x>>a[i].y;
    }
    sort(a+1,a+1+k,cmp);
    for(int i=1;i<=k;i++)
    {
        ll n1=a[i].x;
        ll n2=a[i].y;
        dp[i]=cal(n1+n2,n1);
    }
    ll ans=0;
    for(int i=1;i<=k;i++)
    {
        ll n1=n-a[i].x;
        ll n2=m-a[i].y;
        ll od=cal(n1+n2,max(n1,n2));
        ll op=dp[i]*od; op%=mod;
       // cout<
        ans+=op; ans%=mod;
        for(int j=i+1;j<=k;j++)
        {
            if(a[j].y<a[i].y||a[j].x<a[i].x)
            {
                continue;
            }
            n1=a[j].y-a[i].y;
            n2=a[j].x-a[i].x;
            ll ow=cal(n1+n2,max(n1,n2));
           // cout<
            ow=ow*dp[i];    ow%=mod;
            dp[j]-=ow;
            dp[j]%=mod; dp[j]+=mod; dp[j]%=mod;
            if(dp[j]<0)
                dp[j]+=mod;
        }
        //cout<
    }
    ans%=mod;   ans+=mod;   ans%=mod;
    cout<<ans<<endl;
    return 0;
}