单层感知器简要说明
概念
单层感知器算法是神经网络算法中结构最简单的模型,作为一种线性分类器,它可以对两种类型进行线性分类。感知器是生物神经细胞的简单抽象,是神经网络的原型,是以最简单的方式模拟人类神经元的算法。
神经元图示:
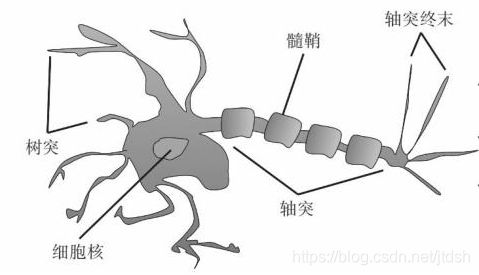
算法模型图示:
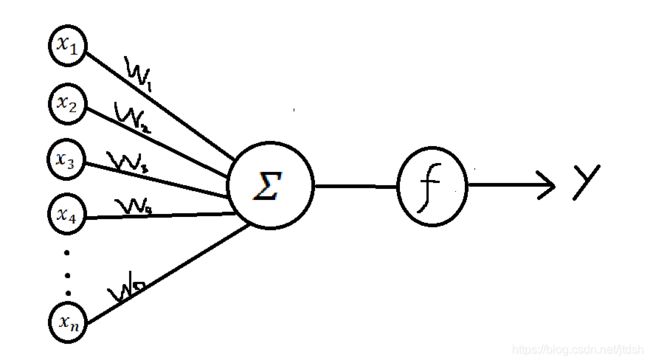
x i x_i xi表示输入信号,是根据预先定义的特征工程的非线性转换, w i w_i wi表示每一种输入信号对应的权重,y表示输出信号。f是激活函数, Σ \varSigma Σ表示的是对所有输入数据的求和。
这样一来就有如下等式:
z = w 1 ∗ x 1 + w 2 ∗ x 2 + w 3 ∗ x 3 . . . . . . w n ∗ x n = w T ∗ x \begin{aligned} z&=w_1*x_1+w_2*x_2+w_3*x_3... ...w_n*x_n\\ &=\bold{w}^T*\bold{x} \end{aligned} z=w1∗x1+w2∗x2+w3∗x3......wn∗xn=wT∗x
其中
w T = [ w 1 w 2 w 3 . . . w n ] T \bold{w}^T=\begin{bmatrix} w_1 \\ w_2\\ w_3\\ ...\\ w_n \end{bmatrix}^T wT=⎣⎢⎢⎢⎢⎡w1w2w3...wn⎦⎥⎥⎥⎥⎤T, x = [ x 1 x 2 x 3 . . . x n ] \bold{x}=\begin{bmatrix} x_1\\x_2\\x_3\\...\\x_n \end{bmatrix} x=⎣⎢⎢⎢⎢⎡x1x2x3...xn⎦⎥⎥⎥⎥⎤.
那么感知器的输出表示为:
y ( x ) = f ( z ) = f ( w T x ) y(x)=f(z)=f(\bold{w}^T\bold{x}) y(x)=f(z)=f(wTx)
而 f ( z ) = { + 1 , z ≥ 0 − 1 z < 0 f(z)=\begin{dcases} +1, &z\geq0 \\ -1 &z<0 \end{dcases} f(z)={+1,−1z≥0z<0
其中 f ( z ) f(z) f(z)被称之为阶跃函数。以上公式的表达的意思是感知器返回的输出是每个特征乘以其对应的权重,然后求和,再将所求和作为阶跃函数的激活输入。其输出结果就是感知器的判断结果。训练过程中,你需要比较计算结果和正确的数据,并反馈错误的情况。
另外,由上面等式可以得出,当 z ≥ 0 z\geq0 z≥0时, f ( z ) = 1 ≥ 0 f(z)=1\geq0 f(z)=1≥0;当 z < 0 z<0 z<0时, f ( z ) = − 1 < 0 f(z)=-1<0 f(z)=−1<0;所以对于每个恰当分类的数据,它都符合下面的等式: w T x n y n > 0 \bold{w}^T\bold{x_n}y_n>0 wTxnyn>0
对于错误的分类,那么也就有 − w T x n y n > 0 -\bold{w}^T\bold{x_n}y_n>0 −wTxnyn>0,
因此可以通过最小化下面的函数来增大感知器的准确度(因为当函数值最小时,表示符合错误分类的点也就越少):
E ( w ) = − ∑ n ϵ M w T x n y n E(w)=- \sum_{n \epsilon M}\bold{w}^T\bold{x_n}y_n E(w)=−nϵM∑wTxnyn
其中M为误分类点的集合,这个损失函数就是感知器学习的经验风险函数。感知器学习的策略就是在假设空间中选取损失函数式最小的模型参数w,即感知器模型。
为了最小误差函数,人们引入梯度下降,梯度下降(gradient descent)在机器学习中应用十分的广泛,不论是在线性回归还是Logistic回归中,它的主要目的是通过迭代找到目标函数的最小值,或者收敛到最小值。该公式如下:
w ( k + 1 ) = w ( k ) − n ∇ E ( w ) = w ( k ) + α x n y n w^{(k+1)}=w^{(k)}-n\nabla E(w)=w^{(k)}+\alpha \bold{x_n}y_n w(k+1)=w(k)−n∇E(w)=w(k)+αxnyn
其中k表示算法中的步骤数, α \alpha α是学习速率,是一个调整学习速率的通用算法优化参数。α不能太大也不能太小,太小的话,可能导致迟迟找不到最低点,太大的话,会导致错过最低点!
∇ \nabla ∇读作nabla,是梯度的表示符号,梯度就是分别对每个变量进行微分,然后用逗号分割开,梯度是用<>包括起来,也就是一个向量,所以 ∇ E ( w ) \nabla E(w) ∇E(w)就等于对 w 1 , w 2 . . . w n w_1,w_2...w_n w1,w2...wn进行微分,又由于几个向量的加权和,等于这些向量中每个元素的加权和组成的向量,最后结果就是 − x n y n -\bold{x_n}y_n −xnyn
实例
简单模拟一下单层感知器,可以加深对算法的印象。
场景:假设周末即将到来,你听说在周末有部大片即将上映–《花木兰》,我的女神刘亦菲主演的,在这里表白一下女神,顺便帮她宣传一波,虽然访问少的可伶,哈哈。回到正题,我们要预测你是否会决定去看。首先电影院很远,附近没有近的影院,所以坐地铁要很久,而且你女朋友吃醋了,听说你要去支持刘亦菲,所以不想陪你去,但是天气很好,阴天。也就是说有3个因素会影响你的决定,这3个因素就可以看作是3个输入特征。那你到底会不会去呢?你的个人喜好——你对上面3个因素的重视程度——会影响你的决定。这3个重视程度就是3个权重。
如果你觉得距离远近无所谓,并且不管女朋友去不去了,我就是要支持刘亦菲,而且你很喜欢阴天,凉风习习,那么我们将预测你会去看电影。这个预测过程可以用我们的公式来表示。我们假设结果z大于0的话就表示会去,小于0表示不去。又设3个特征(x1,x2,x3)为(0,0,1),最后一个是1,它代表了阴天。又设三个权重(w1,w2,w3)是(2,2,7),最后一个是7表示你很喜欢阴天。那么就有z = (x1 * w1 + x2 * w2 + x3 * w3) = (0 * 2 + 0 * 2 + 1 * 7) = 7。预测结果z是7,7大于0,所以预测你会去看电影。
但是这个结果预测不对,虽然天气很好,但是我觉得女朋友的意见也是很重要的,所以我是不想去的。那么这个时候怎么办呢?机器的学习的过程就是训练-》测试-》更新参数-》训练-》测试。。。直到模型最佳。所以这个时候,我们用梯度下降算法更新权重,公式如下这同样可以用我们的公式来表示。
w ( 1 ) = w ( 0 ) − n ∇ E ( w ) w^{(1)}=w^{(0)}-n\nabla E(w) w(1)=w(0)−n∇E(w)
w 0 w^0 w0就是(2,2,7),在这里我们就不算了,我们假设通过公式算的新的权重是(2,7,-1),中间是7表示你挺在乎女朋友的感受的,她不去你也不去,-1表示天气什么的已经不重要了。那么就有z = (x1 * w1 + x2 * w2 + x3 * w3) + b = (0 * 2 + 0 * 7 + 1 * (-1) = -1。预测结果z是-1,-1小于0,所以预测你不会去,会呆在家里陪女朋友,但是心里还在想着花木兰,哈哈。
实际过程肯定不会这么简单的,这个实例就是忽略一些其他的因素,突出主要的内容,加深大家对这个算法的理解。