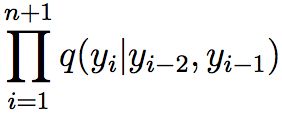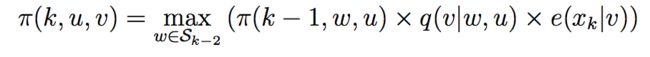Micheal Collins nlp课程笔记（二）Tagging Problems and Hidden Markov Models

一、The Tagging Problem

典型的标签问题有两种：POS（Part Of Speech）和NER（Named Entity Recognition），两者基本一致，POS是给句子的单词打上词性的标签，NER是给句子的单词打上类别的标签（实体或者非实体？实体的话是什么实体等等）

二、生成模型

在Tagging Problem中，我们目标是给定一个句子，能够得到相应的标签序列。因此我们需要训练一个函数f，能够将输入x，映射到输出标签y上。

假设有训练样本x(i), y(i) for i = 1 . . . m. 要找到一个函数f(x)映射到标签,

其中：

但是P(y|x)不好求，因此我们进行一系列数学推到：

       首先从有乘法公式P(x,y) = P(x|y)*P(y) = P(y|x)*P(x)

       可得 ：

       原来的f(x)转为求解使上面这个式子最大值的y。再经过观察发现P(x)与y无关，于是式子进一步简化：

       

至此我们有了函数f(x)了。它主要由两项构成：P(y)和P(x|y)。

先看P(y)，如果抛开句子，只看标签序列，那么问题就和上讲的language Modeling 问题很类似了。就是一个算序列y的概率问题。

根据上讲，假设标签只与前两个标签有关，那么P(y)值就是：

接下来看P(x|y)，在这里我们再次进行了一个大胆的假设，即：x的标签只与本身有关，与其他单词无关，因此P(x|y)值如下：

由此得：

我们的目标就是找到使上式最大的y序列。这个式子也叫做Trigram HMM，Trigram是因为对于式子前半部分我们用了Trigram模型，HMM是因为y序列是隐藏的，我们观察不到，我们只能看到x序列，同时我们又对y进行了马尔科夫假设，因此叫做HMM。

对于上式前半部分，我们可以用Language Modeling中的线性插值法求解q(yi|yi-2,yi-1)。

对于后半部分，最简单粗暴的方法是c(xi,yi)/c(yi)，c表示数量。即用yi标签中是单词xi的次数除以yi标签的次数。

这样做有一个非常严重的问题，即：对于训练集中未出现的x，那么它的这一项将始终为0，由此它的p(x,y)将始终为0。概率一直未0还怎么给它标签？？？所以我们需要改进做法。

改进方法有很多，课程中提到的方法就是，将词分为高频和低频词两类。对于低频词（譬如出现次数小于5的词），将它们映射到一些有限的词类中，然后以词类代表这个词。一个例子如下：

至此模型是差不多了。

三、Viterbi算法

由模型可知，我们的核心问题是给定x1...xn求y序列：

一种最简单的方法当然就是蛮力法，算出所有可能的y序列对应的p(x,y)。可能的y序列将有|S|^n个，代价太大。

因此我们使用Viterbi算法，这个算法的精髓在于递归。

π可以递归定义：

直观理解就是当前位置k最可能的结果是k-1最可能的结果的基础上当前位置各个标签的概率的最大值。

有了递归定义，意味着可以节省很多计算了，只要找到k-1的最大值，那么k的最大值在k-1基础上做就行。

但是，别忘了我们可不是单纯为了求最大值，我们的目标是为了求出y序列，因此，我们还需要一个反向指针记录路径

完整的Viterbi算法如下：

Viterbi的时间复杂度：第一个for循环n，第二个for循环找u、v是|S|^2，for循环里w又是|S|，因此时间复杂度O(n*|S|^3)

四、优缺点

模型简单、表现优良，但是对于e(xi|yi)，如果单词复杂，则处理也很复杂，有时可能需要人工干预。