联合个人训练赛 B 最小子段和

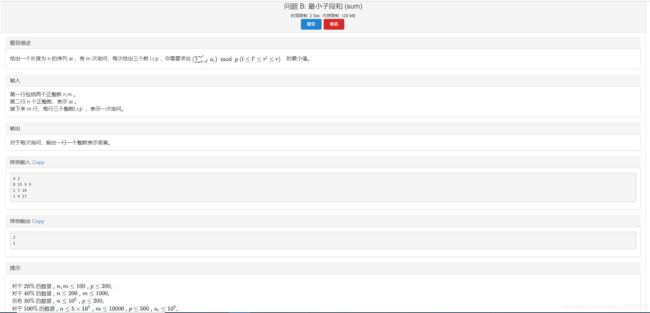
题意如图。
思路：
1 先暴力枚举端点 复杂度(mnn) 过40分

#include
using namespace std;
const int N=1e3+15;
typedef long long ll;
ll a[N],s[N];
int main()
{
    ll n,m,l,r,p;
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        cin>>a[i];
        s[i]=s[i-1]+a[i];
        //s[i]%=mod;
    }
    for(int i=1;i<=m;i++)
    {
        cin>>l>>r>>p;
        ll ans=1123456789123456;
        for(int j=l;j<=r;j++)
        {
            for(int k=j;k<=r;k++)
            {
                ll op=s[k]-s[j-1];
                op%=p;
                ans=min(ans,op);
            }
        }
        cout<<ans<<endl;
    }
    return 0;
}

思路二 ：
在枚举过程中，采取动态更新的方法。
我们发现在这一段区间[l,r]上，当前枚举到点k，如果是暴力，他要利用他前面(k-l)个元素来进行更新。但是完全没必要如此，因为他前面一共最多(0-500)个元素，所以我们可以选择500而不是(k-l)个元素,这在n比较长时很好的优化一些。复杂度 看起来是(m * n * p)，但真是这样吗？下面揭晓。
不过我这时的代码有些问题，好像是空间问题，应该也能优化，但是写不下去了。

#include
using namespace std;
const int N=1e5+150;
typedef long long ll;
int a[N],ans[N],len[N]={0};
int l[510][N],r[510][N], cnt[510][N];
int main()
{
    int n,m,Ll,rr,p,x,id;
    //vectorv;
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        cin>>a[i];
    }
    for(int i=1;i<=m;i++)
    {
        cin>>Ll>>rr>>p;
        len[p]++;
        cnt[p][len[p]]=i;
        l[p][len[p]]=Ll;
        r[p][len[p]]=rr;
    }
    for(p=1;p<=500;p++)
    {
        for(int i=1;i<=len[p];i++)
        {
            id=cnt[p][i];rr=r[p][i]; Ll=l[p][i];
            //cout<
            x=a[rr]%p;
            if(x==0){
                ans[id]=0;  continue;
            }
            vector<int>v;
            v.push_back(x);
            ans[id]=x;
           // cout<
            for(int j=rr-1;j>=Ll;j--)
            {
               // cout<<"**"<
                x=a[j]%p;
                ans[id]=min(ans[id],x);
                if(x==0)    {    ans[id]=0;break;   }
                vector<int>v1;
                v.push_back(x);
                while(!v.empty())
                {
                    x=v.front();   v.pop_back();
                   // cout<<"?"<
                    x=(x+a[j])%p;   v1.push_back(x);
                    //cout<
                    ans[id]=min(ans[id],x);
                    if(x==0)       break;
                }
                if(ans[id]==0)    break;
                //cout<<"!!!"<
                while(!v1.empty())
                {
                    x=v1.front();
                  //  cout<<"!"<
                    v.push_back(x);  v1.pop_back();
                }
            }
        }
    }
    for(int i=1;i<=m;i++)
    {
        cout<<ans[i]<<endl;
    }
    return 0;
}

思路3：
我们发现当ans[i]==0时可以跳出循环，这对我们的程序的优化有很大的作用。利用这个，思路一的代码能多跑20分，思路二代码正确的话应该能过。
首先我们继续考虑思路二的真实复杂度。
上面说可能是 m * len * p。 一般最坏len=n,所以写m * n * p;
m是查询数，len是每次要查询的长度的区间，p是每个点由上一个点更新而来的状态。
但是我们的len真的会走到n嘛？ 不可能。

看上面代码的第三个for循环，看v的更新，发现在每一次j--，
v里面一定会多出现一个元素，即他自己，和用他更新的v之前存在的元素。
为什么每次都会多一个呢，因为如果不会多一个，v里面一定有0的存在。
这样想，用a去更新之前的存在，那些之前的存在的数的种类不会少，只是变了变值。
然后再加上一个a[j]，发现元素没有增加，肯定是因为里面也有a[j]这个值。
那么a[j]加谁才会出现a[j]呢,是0。
所以那时候v里面肯定有0了。有0就代表我们可以输出答案跳出循环了。

在上面一段我们已经证明了len的长度最坏是p,而不是n。因为v里面每次容量加1，但是他的上限是mpp，时间复杂度2e7。所以思路二时间复杂度没有问题，但是空间我给写坏了，但是也没必要改了，因为我们此时发现了一个更优的性质。
即我们需要枚举的长度大于p，即可输出0。
这个性质在上面已经证明了。然后我们发现利用这个，之前第一步的暴力的复杂度也变成了mpp，那就可以过了。不过被卡常了，加了一点优化。
其实应该刚开始就想到的，刚开始先想p=1时任意数都为0，当p为2时，长度为3就肯定是。如（121）（212），当时再想一下p = 3，估计也就直接发现这个性质了。
以前打cf也经常这样只考虑奇偶，n = 1,n = 2什么的，下次一定多写几个，写到5.。。。。。。。。（昨天的欧拉函数可能是因为给到了7才过的。。。）
代码：

#pragma GCC optimize(2)
#pragma GCC optimize("Ofast","unroll-loops","omit-frame-pointer","inline")
#include
using namespace std;
const int N=1e6+15;
typedef long long ll;
int a[N];
ll s[N];
int main()
{
    int n,m,l,r,p;
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&a[i]);
        s[i]=s[i-1]+a[i];
        //s[i]%=mod;
    }
    for(int i=1;i<=m;i++)
    {
        scanf("%d%d%d",&l,&r,&p);
        if(p==1)
        {
            cout<<"0"<<endl;
            continue;
        }
        if(r-l>p)
        {
            printf("0\n");
            continue;
        }
        int ans=1123456789;
        for(int j=l;j<=r;j++)
        {
            for(int k=j;k<=r;k++)
            {
                ll op=s[k]-s[j-1];
                op%=p;
                ans=min(ans,int(op));
                if(ans==0)
                    break;
            }
        }
        printf("%d\n",ans);
    }
    return 0;
}