CTF密码学部分知识总结(一)
目录
- openssl 解密RSA一般步骤
- 1.凯撒密码(Caesar)
- 2.摩斯密码在线解密
- 3.unicode在线解码
- 4.栅栏密码在线解密
- 5.培根密码在线解密
- 6.python反编译工具uncompyle
- 7.Easy-RSA
- 8.将ASC码值转换成字符
- 9.RSA共模攻击
- 10.Wiener’s attack的条件
- 10.16进制转字符串
- 11.RSA题目总结
- 给了公钥的文件解密
- 已知n(n=p*q),e和被公钥加密的密文,求原文
- 已知两组公钥和密文,但不共模,求flag
- 共模解密方法:
- ASCII text文件读取
- 维吉利亚密码破解
- ROT13解密
- Poemcode解密
- 公钥私钥总结
openssl 解密RSA一般步骤
步骤:
①使用 openssl 解密.pem 中参数 --> ②参数十六进制转换为十进制 --> ③ 利用 factor 对大整数进行分解,得到 p 和 q --> ④用 rsatool 生成私钥文件: private.pem --> ⑤用 private.pem 解密 flag.enc
①使用 openssl 解密.pem 中参数。
Openssl 是 linux 自带的一个加密库,可以直接使用。
openssl rsa -pubin -text -modulus -in warmup -in ./Normal_RSA/pubkey.pem
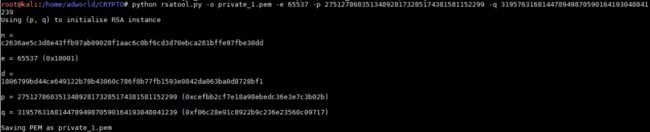
②参数十六进制转换为十进制 Python 支持直接将 16 进制转换为 10 进制 Linux 下进入 python 命令行 0x C2636AE5C3D8E43FFB97AB09028F1AAC6C0BF6CD3D70EBCA281BFFE97FBE30DD

也可使用python solve.py -g --dumpkey --key ../exercise/rsa-2/public.pem,得到的n直接是十进制的,可以省略步骤1和2
③利用 factor 对大整数进行分解,得到 p 和 q :
p= 275127860351348928173285174381581152299
q= 319576316814478949870590164193048041239
④用 rsatool 生成私钥文件: private.pem
python rsatool.py -o private.pem -e 65537 -p 275127860351348928173285174381581152299 -q 319576316814478949870590164193048041239
openssl rsautl -decrypt -in ./Normal_RSA/flag.enc -inkey ./private_1.pem
![]()
成功获取flag,这种方法比较啰嗦,作为用来弥补solve.py无法获取完整flag的情况,接下来总结常用的各种密码学解密方法:
1.凯撒密码(Caesar)
#!/usr/bin/python
# -*- coding=utf -*-
def caesar(cipher):
for j in range(26):
str_list = list(cipher)
i = 0
while i < len(cipher):
if not str_list[i].isalpha():
str_list[i] = str_list[i]
else:
a = "A" if str_list[i].isupper() else "a"
str_list[i] = chr((ord(str_list[i]) - ord(a) + j) % 26 + ord(a))
i = i + 1
print(''.join(str_list))
if __name__ == '__main__':
cipher = "oknqdbqmoq{kag_tmhq_xqmdzqp_omqemd_qzodkbfuaz}"
caesar(cipher)
2.摩斯密码在线解密
http://www.bejson.com/enc/morse/
# !/usr/bin/python
# -*- coding=utf -*-
table = {'a': ".-", 'b': "-...", 'c': "-.-.", 'd': "-..", 'e': ".", 'f': "..-.", 'g': "--.",
'h': "....", 'i': "..", 'j': ".---", 'k': "-.-", 'l': ".-..", 'm': "--", 'n': "-.",
'o': "---", 'p': ".--.", 'q': "--.-", 'r': ".-.", 's': "...", 't': "-", 'u': "..-",
'v': "...-", 'w': ".--", 'x': "-..-", 'y': "-.--", 'z': "--..",
'0': '-----', '1': '.----', '2': '..---', '3': '...--', '4': '....-',
'5': '.....', '6': '-....', '7': '--...', '8': '---..', '9': '----.',
',': '--..--', '.': '.-.-.-', ':': '---...', ';': '-.-.-.',
'?': '..--..', '=': '-...-', "'": '.----.', '/': '-..-.',
'!': '-.-.--', '-': '-....-', '_': '..--.-', '(': '-.--.',
')': '-.--.-', '$': '...-..-', '&': '. . . .', '@': '.--.-.'}
def morse(cipher):
msg = ''
codes = cipher.split(' ')
for code in codes:
if code == '':
msg += ' '
else:
UNCODE = dict(map(lambda t: (t[1], t[0]), table.items()))
msg += UNCODE[code]
return msg
if __name__ == '__main__':
# file = open(r'D:\CTF\攻防世界\Crypto\Morse.txt', 'r')
# cipher = file.read()
cipher ="11 111 010 000 0 1010 111 100 0 00 000 000 111 00 10 1 0 010 0 000 1 00 10 110"
cipher = cipher.replace('1', '-')
cipher = cipher.replace('0', '.')
plaintext = morse(cipher)
print(plaintext)
3.unicode在线解码
https://www.css-js.com/tools/unicode.html
ASC2码如下
Unicode特征如下:
最后解码到这里之后不会解码了
/119/101/108/99/111/109/101/116/111/97/116/116/97/99/107/97/110/100/100/101/102/101/110/99/101/119/111/114/108/100
照搬大神的程序
import base64
# a = open(r'crypto8.txt','r')
# s = a.read()
s="JiM4NDsmIzEwNzsmIzExODsmIzc3OyYjODQ7JiM2OTsmIzEyMDsmIzc2OyYjMTIyOyYjNjk7JiMxMjA7JiM3ODsmIzY3OyYjNTY7JiMxMjA7JiM3NzsmIzY4OyYjMTAzOyYjMTE4OyYjNzc7JiM4NDsmIzY1OyYjMTE5Ow=="
# base64解密一下
b = base64.b64decode(s).decode('ascii')
# 对解密后的字符串进行处理
b = b.strip('&#;')
c = []
c = b.split(';&#')
# unicode解密
d = ''
for i in c:
d += chr(int(i))
# base64再次解密
e = base64.b64decode(d).decode('ascii')
# 对字符进行处理
e = e.strip('/')
f = []
f = e.split('/')
# 转化为ascii码
flag =''
for i in f:
flag += chr(int(i))
print('flag is ',flag)
4.栅栏密码在线解密
http://www.atoolbox.net/Tool.php?Id=777
5.培根密码在线解密
# !/usr/bin/python
# -*- coding=utf -*-
import re
table = {'a': 'aaaaa', 'b': 'aaaab', 'c': 'aaaba', 'd': 'aaabb', 'e': 'aabaa', 'f': 'aabab', 'g': 'aabba',
'h': 'aabbb', 'i': 'abaaa', 'j': 'abaab', 'k': 'ababa', 'l': 'ababb', 'm': 'abbaa', 'n': 'abbab',
'o': 'abbba', 'p': 'abbbb', 'q': 'baaaa', 'r': 'baaab', 's': 'baaba', 't': 'baabb', 'u': 'babaa',
'v': 'babab', 'w': 'babba', 'x': 'babbb', 'y': 'bbaaa', 'z': 'bbaab'}
def bacon(cipher):
msg = ''
codes = re.findall(r'.{5}', cipher)
for code in codes:
if code == '':
msg += ' '
else:
UNCODE = dict(map(lambda t: (t[1], t[0]), table.items()))
msg += UNCODE[code]
return msg
if __name__ == '__main__':
cipher = 'AAAAABAABBBAABBAAAAAAAABAABABAAAAAAABBABAAABBAAABBAABAAAABABAABAAABBABAAABAAABAABABBAABBBABAAABABABBAAABBABAAABAABAABAAAABBABBAABBAABAABAAABAABAABAABABAABBABAAAABBABAABBA'
# cipher = cipher.upper()
cipher = cipher.lower()
plaintext = bacon(cipher)
print(plaintext)
6.python反编译工具uncompyle
python的.pyc文件,大致可以理解为python程序编译后得到的文件。可以下载uncompyle库后使用uncompyle6将easychallenge.pyc反编译成py文件。
uncompyle6 easychallenge.pyc > easychallenge.py
7.Easy-RSA
RSA 的算法涉及三个参数,n、e、d。 应用流程
选取两个较大的互不相等的质数p和q,计算n = p * q。
计算phi = (p-1) * (q-1) 。
选取任意e,使得e满足 1
加解密:
c = (m ^ e) % n
m = (c ^ d) % n
其中m为明文,c为密文,(n,e)为公钥对,d为私钥,要求 0 <= m < n。
GCD是求最大公约数的一种方法
其中,n 是两个大质数 p、q 的积,n 的二进制表示所占用的位数就是所谓的密钥长度。 e 和 d 是一对相关的值,e 可以任意取,但要求 e 与(p-1)(q-1)互质;再选择 d,要求(de)mod((p-1)*(q-1))=1。 (n,e),(n,d)就是密钥对。其中(n,e)为公钥,(n,d)为私钥。 RSA 加解密的算法完全相同,设 A 为明文,B 为密文,则:A=B^d mod n;B=A^e mod n;(公钥加密体制 中,一般用公钥加密,私钥解密) e 和 d 可以互换使用,即: A=B^d mod n;B=A^e mod n 直接给了 p,q,e,求 d,即为暴力破解 RSA 的私钥之一的 d
可以使用这款工具:https://github.com/3summer/CTF-RSA-tool
python solve.py --verbose --private -N 2135733555619387051 -e 17 -p 473398607161 -q 4511491
得到的d值就是FLAG
python solve.py --verbose -k examples/jarvis_oj_mediumRSA/pubkey.pem --decrypt examples/jarvis_oj_mediumRSA/flag.enc
关于solve.py工具的介绍可以参考
https://www.freebuf.com/articles/others-articles/161475.html
8.将ASC码值转换成字符
import re
r="/119/101/108/99/111/109/101/116/111/97/116/116/97/99/107/97/110/100/100/101/102/101/110/99/101/119/111/114/108/100"
r=re.split("/",r)
flag=""
for i in range(1,len(r)):
flag=flag+chr(int(r[i]))
print flag
9.RSA共模攻击
假设有一家公司COMPANY,在员工通信系统中用RSA加密消息。COMPANY首先生成了两个大质数P,Q,取得PQ乘积N。并且以N为模数,生成多对不同的公钥及其相应的私钥。COMPANY将所有公钥公开。而不同的员工获得自己的私钥,比如,员工A获得了私钥d1.员工B获得了私钥d2.
现在,COMPANY将一条相同的消息,同时经过所有公钥加密,发送给所有员工。此时,就可能出现共模攻击。
共模攻击也称同模攻击,英文原名是 Common Modulus Attack 。同模攻击利用的大前提就是,RSA体系在生成密钥的过程中使用了相同的模数n。
如果,此时有一个攻击者,同时监听了A和B接收到的密文c1,c2,因为模数不变,以及所有公钥都是公开的,那么利用同模攻击,他就可以在不知道d1,d2的情况下解密得到消息m。
参考链接:https://www.jianshu.com/p/9b44512d898f
import gmpy2
def ByteToHex( bins ):
return ''.join( [ "%02X" % x for x in bins ] ).strip()
def n2s(num):
t = hex(num)[2:]
if len(t) % 2 == 1:
t = '0'+ t
return ''.join([chr(int(b, 16)) for b in [t[i:i+2] for i in range(0, len(t), 2)]])
n = 0x00b0bee5e3e9e5a7e8d00b493355c618fc8c7d7d03b82e409951c182f398dee3104580e7ba70d383ae5311475656e8a964d380cb157f48c951adfa65db0b122ca40e42fa709189b719a4f0d746e2f6069baf11cebd650f14b93c977352fd13b1eea6d6e1da775502abff89d3a8b3615fd0db49b88a976bc20568489284e181f6f11e270891c8ef80017bad238e363039a458470f1749101bc29949d3a4f4038d463938851579c7525a69984f15b5667f34209b70eb261136947fa123e549dfff00601883afd936fe411e006e4e93d1a00b0fea541bbfc8c5186cb6220503a94b2413110d640c77ea54ba3220fc8f4cc6ce77151e29b3e06578c478bd1bebe04589ef9a197f6f806db8b3ecd826cad24f5324ccdec6e8fead2c2150068602c8dcdc59402ccac9424b790048ccdd9327068095efa010b7f196c74ba8c37b128f9e1411751633f78b7b9e56f71f77a1b4daad3fc54b5e7ef935d9a72fb176759765522b4bbc02e314d5c06b64d5054b7b096c601236e6ccf45b5e611c805d335dbab0c35d226cc208d8ce4736ba39a0354426fae006c7fe52d5267dcfb9c3884f51fddfdf4a9794bcfe0e1557113749e6c8ef421dba263aff68739ce00ed80fd0022ef92d3488f76deb62bdef7bea6026f22a1d25aa2a92d124414a8021fe0c174b9803e6bb5fad75e186a946a17280770f1243f4387446ccceb2222a965cc30b3929
e1 = 17
e2 = 65537
s = gmpy2.gcdext(e1,e2) #gmpy2.gcdext(e1,e2)的运行结果为元组(mpz(1), mpz(30841), mpz(-8)),所以元组的第0个值不能取,第1个值才是s1,第2个值由于是负数,所以要取反,变为正数
s1 = s[1]
s2 = -s[2]
file1 = open("E:/04 CTF/i春秋/ISC2016训练赛——phrackCTF/Crypto-very hard RSA/veryhardRSA/flag.enc1" ,'rb').read()
c1 = int(ByteToHex(file1),16)
file2 = open("E:/04 CTF/i春秋/ISC2016训练赛——phrackCTF/Crypto-very hard RSA/veryhardRSA/flag.enc2" ,'rb').read()
c2 = int(ByteToHex(file2),16)
c2 = gmpy2.invert(c2, n) #由于根据前面的运算,s1是正数,s2是负数,后面需要运算c2的s2次幂。因为在数论模运算中,要求一个数的负数次幂,与常规方法并不一样,比如此处要求c2的s2次幂,就要先计算c2的模反元素c2r,然后求c2r的-s2次幂。
m = (pow(c1,s1,n) * pow(c2 , s2 , n)) % n
print(n2s(m))
这样子很麻烦,用libnum库自带的n2s和s2n函数来代替代码里的n2s和ByteToHex函数,这里附上一个简单的将公钥加密的文本转换成数字的小程序:
import libnum
f=open("flag.enc1",'rb')
c1=libnum.s2n(f.read())
print(c1)
得到c的数值表示后我们配置好参数文件直接使用下面的脚本解密得到flag
python solve.py -i ../exercise/veryhardRSA/share_N.txt
10.Wiener’s attack的条件
e很大的,d可能就会比较小,可能会满足Wiener’s attack的条件
Wiener’s attack
python solve.py --verbose --private -i examples/wiener_attack.txt
或者通过命令行,只要指定对应参数就行了
python solve.py --verbose --private -N
460657813884289609896372056585544172485318117026246263899744329237492701820627219556007788200590119136173895989001382151536006853823326382892363143604314518686388786002989248800814861248595075326277099645338694977097459168530898776007293695728101976069423971696524237755227187061418202849911479124793990722597
-e 354611102441307572056572181827925899198345350228753730931089393275463916544456626894245415096107834465778409532373187125318554614722599301791528916212839368121066035541008808261534500586023652767712271625785204280964688004680328300124849680477105302519377370092578107827116821391826210972320377614967547827619
10.16进制转字符串
http://www.bejson.com/convert/ox2str/
11.RSA题目总结
已知p,q,e,c四个参数:
from Crypto.Util.number import *
import gmpy2
import binascii
import hashlib
import base64
p=0xa6055ec186de51800ddd6fcbf0192384ff42d707a55f57af4fcfb0d1dc7bd97055e8275cd4b78ec63c5d592f567c66393a061324aa2e6a8d8fc2a910cbee1ed9
q=0xfa0f9463ea0a93b929c099320d31c277e0b0dbc65b189ed76124f5a1218f5d91fd0102a4c8de11f28be5e4d0ae91ab319f4537e97ed74bc663e972a4a9119307
e=0x6d1fdab4ce3217b3fc32c9ed480a31d067fd57d93a9ab52b472dc393ab7852fbcb11abbebfd6aaae8032db1316dc22d3f7c3d631e24df13ef23d3b381a1c3e04abcc745d402ee3a031ac2718fae63b240837b4f657f29ca4702da9af22a3a019d68904a969ddb01bcf941df70af042f4fae5cbeb9c2151b324f387e525094c41
c=0x7fe1a4f743675d1987d25d38111fae0f78bbea6852cba5beda47db76d119a3efe24cb04b9449f53becd43b0b46e269826a983f832abb53b7a7e24a43ad15378344ed5c20f51e268186d24c76050c1e73647523bd5f91d9b6ad3e86bbf9126588b1dee21e6997372e36c3e74284734748891829665086e0dc523ed23c386bb520
pvi=(p-1)*(q-1)
n=q*p
d=gmpy2.invert(e,pvi)
print binascii.unhexlify(hex(pow(c,d,n))[2:])
已知RSA的公钥和密文,直接使用solve.py 解密
python solve.py -k ./cry200/key.pem --decrypt ./cry200/cipher.bin
ECCTools可以用来椭圆曲线加密分析,注意上来要选择合适的进制

给了公钥的文件解密
OpenSSL 使用 PEM 文件格式存储证书和密钥。PEM 实质上是 Base64 编码的二进制内容,再加上开始和结束行
如证书文件的 -----BEGIN CERTIFICATE----- 和 -----END CERTIFICATE----- 在这些标记外面可以有额外的信息,如编码内容的文字表示。文件是 ASCII 的,可以用任何文本编辑程序打开它们。

解题思路:①使用 openssl 解密.pem 中参数 --> ②参数十六进制转换为十进制 --> ③ 利用 factor 对大整数进行分解,得到 p 和 q --> ④用 rsatool 生成私钥文件: private.pem --> ⑤用 private.pem 解密 flag.enc,详细使用过程参考片头
已知n(n=p*q),e和被公钥加密的密文,求原文
from Crypto.PublicKey import RSA
import Crypto.Cipher.PKCS1_OAEP
import gmpy2, base64
pub = open("key.pub", "r").read()
pub = RSA.importKey(pub)
n = long(pub.n)
print "n"
print n
e = long(pub.e)
print "e"
print e
#w/ n, get p and q from factordb.com
p = 863653476616376575308866344984576466644942572246900013156919
print "p"
print p
q = 965445304326998194798282228842484732438457170595999523426901
print "q"
print q
d = long(gmpy2.invert(e,(p-1)*(q-1)))
print "d"
print d
key = RSA.construct((n,e,d))
secret = base64.b64decode("Ni45iH4UnXSttNuf0Oy80+G5J7tm8sBJuDNN7qfTIdEKJow4siF2cpSbP/qIWDjSi+w=")
print key.decrypt(secret)
更为简洁的程序,手动配置所有参数
from Crypto.Util.number import *
import Crypto.Cipher.PKCS1_OAEP
from Crypto.PublicKey import RSA
import gmpy2, base64
import libnum
e = long(65537)
print "e"
print e
n=long(76775333340223961139427050707840417811156978085146970312315886671546666259161)
#w/ n, get p and q from factordb.com
p = 273821108020968288372911424519201044333
q = 280385007186315115828483000867559983517
d = long(gmpy2.invert(e,(p-1)*(q-1)))
print "d"
print d
key = RSA.construct((n,e,d))
c1=bytes_to_long(open('./fllllllag.txt','rb').read())
print("answer")
print libnum.n2s(key.decrypt(c1))
已知两组公钥和密文,但不共模,求flag
#!python2
import gmpy2
from Crypto.Util.number import *
from Crypto.PublicKey import RSA
f = open("pubkey1.pem", "r")
key = RSA.importKey(f.read())
n1=key.n
e1=key.e
print ('N1=',n1)
print ('E1=',e1) #然后分解N
f = open("pubkey2.pem", "r")
key = RSA.importKey(f.read())
n2=key.n
e2=key.e
print ('N2=',n2 )
print ('E2=',e2)
p1=95652716952085928904432251307911783641637100214166105912784767390061832540987
q1=107527961531806336468215094056447603422487078704170855072884726273308088647617
p2=89485735722023752007114986095340626130070550475022132484632643785292683293897
q2=95652716952085928904432251307911783641637100214166105912784767390061832540987
phi1=(p1-1)*(q1-1)
c1=4314251881242803343641258350847424240197348270934376293792054938860756265727535163218661012756264314717591117355736219880127534927494986120542485721347351L
d1=gmpy2.invert(e1,phi1)
m1=gmpy2.powmod(c1,d1,n1)
print hex(m1)[2:].decode('hex')
phi2=(p2-1)*(q2-1)
c2=485162209351525800948941613977942416744737316759516157292410960531475083863663017229882430859161458909478412418639172249660818299099618143918080867132349L
d2=gmpy2.invert(e2,phi2)
m2=gmpy2.powmod(c2,d2,n2)
print hex(m2)[2:].decode('hex')
共模解密方法:
from Crypto.Util.number import *
from Crypto.PublicKey import RSA
import gmpy2
def egcd(a,b):
if b==0:
return a,1,0
else:
g,x,y=egcd(b,a%b)
return g,y,x-a//b*y
c1=bytes_to_long(open('./cipher1.txt','rb').read())
c2=bytes_to_long(open('./cipher2.txt','rb').read())
print(hex(c1))
print(hex(c2))
pub1=RSA.importKey(open('./publickey1.pem').read())
pub2=RSA.importKey(open('./publickey2.pem').read())
n1= pub1.n
e1= pub1.e
n2= pub2.n
e2= pub2.e
assert n1==n2
s1=gmpy2.invert(e1,e2)
s2=egcd(e1,e2)[2]
if(s1<0):
s1=-s1
c1=gmpy2.invert(c1,n1)
if(s2<0):
s2=-s2
c2=gmpy2.invert(c2,n1)
m=long_to_bytes((pow(c1,s1,n1)*pow(c2,s2,n1))%n1)
print(m)
ASCII text文件读取
from Crypto.Util.number import *
import libnum
c2=bytes_to_long(open('./cr2-many-time-secrets','rb').read())
print(c2)
libnum.n2s(c2)
题目中给了十几个用同一一次密码本加密的内容,使用many time pad attack进行解密
参考网址:https://www.dazhuanlan.com/2019/12/16/5df68e0bb9ad4/
## OTP - Recovering the private key from a set of messages that were encrypted w/ the same private key (Many time pad attack) - crypto100-many_time_secret @ alexctf 2017
# @author intrd - http://dann.com.br/
# Original code by jwomers: https://github.com/Jwomers/many-time-pad-attack/blob/master/attack.py)
import string
import collections
import sets, sys
# 11 unknown ciphertexts (in hex format), all encrpyted with the same key
c1 = "0529242a631234122d2b36697f13272c207f2021283a6b0c7908"
c2 = "2f28202a302029142c653f3c7f2a2636273e3f2d653e25217908"
c3 = "322921780c3a235b3c2c3f207f372e21733a3a2b37263b313012"
c4 = "2f6c363b2b312b1e64651b6537222e37377f2020242b6b2c2d5d"
c5 = "283f652c2b31661426292b653a292c372a2f20212a316b283c09"
c6 = "29232178373c270f682c216532263b2d3632353c2c3c2a293504"
c7 = "613c37373531285b3c2a72273a67212a277f373a243c20203d5d"
c8 = "243a202a633d205b3c2d3765342236653a2c7423202f3f652a18"
c9 = "2239373d6f740a1e3c651f207f2c212a247f3d2e65262430791c"
c10 = "263e203d63232f0f20653f207f332065262c3168313722367918"
c11 = "2f2f372133202f142665212637222220733e383f2426386b"
ciphers = [c1, c2, c3, c4, c5, c6, c7, c8, c9, c10, c11]
# The target ciphertext we want to crack
target_cipher = "2239373d6f740a1e3c651f207f2c212a247f3d2e65262430791c"
#target_cipher = "263e203d63232f0f20653f207f332065262c3168313722367918"
# XORs two string
def strxor(a, b): # xor two strings (trims the longer input)
return "".join([chr(ord(x) ^ ord(y)) for (x, y) in zip(a, b)])
# To store the final key
final_key = [None]*150
# To store the positions we know are broken
known_key_positions = set()
# For each ciphertext
for current_index, ciphertext in enumerate(ciphers):
counter = collections.Counter()
# for each other ciphertext
for index, ciphertext2 in enumerate(ciphers):
if current_index != index: # don't xor a ciphertext with itself
for indexOfChar, char in enumerate(strxor(ciphertext.decode('hex'), ciphertext2.decode('hex'))): # Xor the two ciphertexts
# If a character in the xored result is a alphanumeric character, it means there was probably a space character in one of the plaintexts (we don't know which one)
if char in string.printable and char.isalpha(): counter[indexOfChar] += 1 # Increment the counter at this index
knownSpaceIndexes = []
# Loop through all positions where a space character was possible in the current_index cipher
for ind, val in counter.items():
# If a space was found at least 7 times at this index out of the 9 possible XORS, then the space character was likely from the current_index cipher!
if val >= 7: knownSpaceIndexes.append(ind)
#print knownSpaceIndexes # Shows all the positions where we now know the key!
# Now Xor the current_index with spaces, and at the knownSpaceIndexes positions we get the key back!
xor_with_spaces = strxor(ciphertext.decode('hex'),' '*150)
for index in knownSpaceIndexes:
# Store the key's value at the correct position
final_key[index] = xor_with_spaces[index].encode('hex')
# Record that we known the key at this position
known_key_positions.add(index)
# Construct a hex key from the currently known key, adding in '00' hex chars where we do not know (to make a complete hex string)
final_key_hex = ''.join([val if val is not None else '00' for val in final_key])
# Xor the currently known key with the target cipher
output = strxor(target_cipher.decode('hex'),final_key_hex.decode('hex'))
print "Fix this sentence:"
print ''.join([char if index in known_key_positions else '*' for index, char in enumerate(output)])+"n"
target_plaintext = "cure, Let Me know if you a"
print "Fixed:"
print target_plaintext+"n"
key = strxor(target_cipher.decode('hex'),target_plaintext)
print "Decrypted msg:"
for cipher in ciphers:
print strxor(cipher.decode('hex'),key)
print "nPrivate key recovered: "+key+"n"
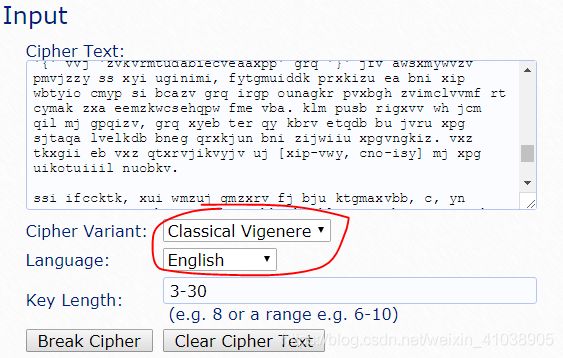
维吉利亚密码破解
直接在网站上暴力破解
https://www.guballa.de/vigenere-solver
ROT13解密
通过上述描述,进行rot13解密:
cat banana-princess.pdf | tr ‘A-Za-z’ ‘N-ZA-Mn-za-m’ > new.pdf
tr是个简单的替换命令,从标准输入中替换、缩减和/或删除字符,并将结果写到标准输出
通过Adobe_Reader复制图像后粘贴到文档中如下:

在这里我们可以看到答案。
可以结合head明令查看文件的头部信息: strings banana-princess.pdf |head
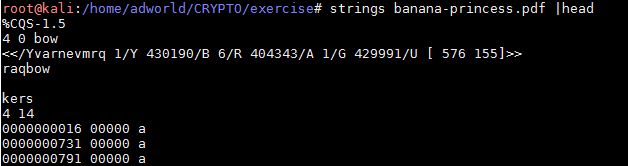
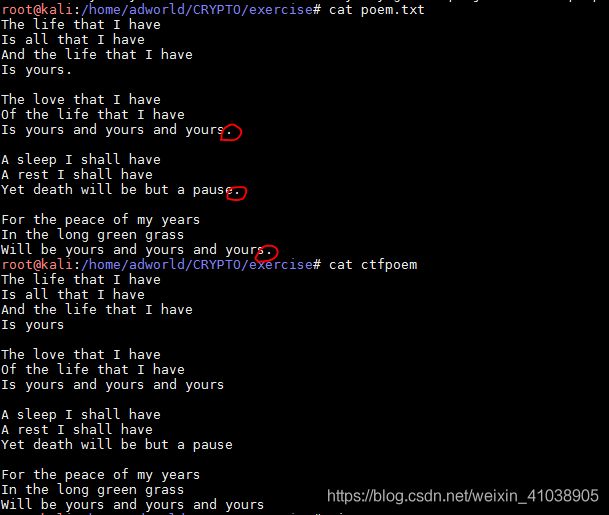
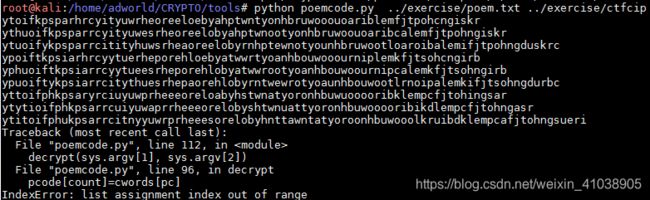
Poemcode解密
公钥私钥总结
from Crypto.PublicKey import RSA
import gmpy2
import base64
from Crypto.Cipher import PKCS1_v1_5 as Cipher_pkcs1_v1_5
public = RSA.importKey(open('public.pem').read())
n = long(public.n)
e = long(public.e)
print n
print e
private = RSA.importKey(open('privatekey.pem').read())
#print '%x' % private.q
print("private.q:",private.q)
**注意这里的p和q不相等,p通过私钥获取,但是我不知道怎么通过私钥获取**
p = 167343506005974003380506069679607737381940204686173214188860057004909006055220516074283090160430833007424970980655748310232878462615469792561310560310363430669700009093597847018287568821792168143170329382585883857083334915378884054389878477389765792275111293420203613159303898365894897865177093362621517279751
#p=long(private.q)
print("*******.q:",p)
q = n / p
d = gmpy2.invert(e, (p-1)*(q-1))
keypair = RSA.generate(1024)
keypair.p = p
keypair.q = q
keypair.e = e
keypair.n = n
phi_n = long((keypair.p-1) * (keypair.q-1))
i = 1
while (True):
x = (phi_n * i ) + 1
if (x % keypair.e == 0):
keypair.d = x / keypair.e
break
i += 1
private = open('private1.pem','w')
private.write(keypair.exportKey())
private.close()
cipher_text = "qzogS7X8M3ZOpkUhJJcbukaRduLyqHAPblmabaYSm9iatuulrHcEpBmil7V40N7gbsQXwYx5EBH5r5V2HRcEIOXjgfk5vpGLjPVxBLyXh2DajHPX6KvbFpQ8jNpCQbUNq8Hst00yDSO/6ri9dk6bk7+uyuN0b2K1bNG5St6sCQ4qYEA3xJbsHFvMqtvUdhMiqO7tNCUVTKZdN7iFvSJqK2IHosIf7FqO24zkHZpHi31sYU7pcgYEaGkVaKs8pjq6nbnffr4URfoexZHeQtq5UAkr95zD6WgvGcxaTDKafFntboX9GR9VUZnHePiio7nJ3msfue5rkIbISjmGCAlj+w=="
f = open('private1.pem','r')
key = RSA.importKey(f.read())
cipher = Cipher_pkcs1_v1_5.new(key)
plain_text = cipher.decrypt(base64.b64decode(cipher_text),'ERROR')
print plain_text
另有总结非常完整的博客可参考:
https://blog.csdn.net/qq_40837276/article/details/83080460