详解DBSCAN聚类算法

1 简介

带噪空间基于密度的聚类方法（Density-Based Spatial Clustering of Applications with Noise，DBSCAN）是一种比较有代表性的基于密度的聚类算法。与划分和层次聚类方法不同，它将簇定义为密度相连的点的最大集合，能够把具有足够高密度的区域划分为簇，并可在带噪声的数据集空间中发现任意形状的类别簇。和K-Means，BIRCH这些一般只适用于凸样本集的聚类相比，DBSCAN既可以适用于凸样本集，也可以适用于非凸样本集。

---

2 算法

DBSCAN是一种基于密度的聚类算法，这类密度聚类算法一般假定类别可以通过样本分布的紧密程度决定。同一类别的样本，他们之间应该是紧密相连的，算法将这样的关系成为密度相连的。算法通过将密度相连的样本划为一类，这样就得到了一个聚类类别。再将所有样本划为多个密度相连的不同类别，就得到了最终的聚类结果。

2.1 定义

定义1：（点的Eps-邻域）点$p$的Eps-邻域 表示样本集合$D$中于点$p$的距离小于$Eps$的所有样本点的集合，用$N_{Eps}(p)$表示，定义为
$$N_{Eps}(p)=\left\{q\in D|dist(p,q)\le Eps\right\}$$

定义2：（核心点）样本点$p$的Eps-邻域 的样本点个数用$\left|N_{Eps}(p)\right|$表示，若其样本点数$\left|N_{Eps}(p)\right|\ge MinPts$，则称样本点$p$为核心点。其余的样本点成为边界点。如下图所示，点$p$为核心点，点$q$为边界点。

定义3：（直接密度可达）若样本点$p$与点$q$满足如下条件：

1. $p\in N_{Eps}(q)$
2. $\left|N_{Eps}(q)\right|\ge MinPts$（核心点条件）

则称点$p$可由点$q$直接密度可达，反之不一定成立。如下图所示，因为点$p$不是核心点，点$q$是核心点，而点$p$又在点$q$的Eps-邻域 内，因此点$p$可由点$q$直接密度可达，点$q$不能由点$p$直接密度可达。

定义4：（密度可达）若有一串点$p_1$、$p_2$、…、$p_N$，其中$p_1\equiv q$，$p_N\equiv p$，而$p_{i+1}$可由$p_i$直接密度可达（$i=1,2,...,N-1$），则称点$p$可由点$q$密度可达。
密度可达性是密度直接可达性的扩展，这是一种传递的关系，但不是对称可逆的，只有核心点对之间的密度可达性是对称的。如下图所示，点$p$可由点$q$密度可达，而点$q$不能由点$p$密度可达。

定义5（密度相连）若有点$o$，使得点$p$和点$q$都由$o$密度可达，那么称点$p$和点$q$是密度相连的。
密度相连性是一种对称可逆的关系。如下图所示，点$p$和点$q$是密度相连的。

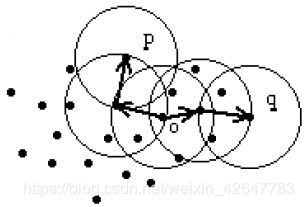
定义6：（簇）设样本集为$D$，那么参数为$Eps$和$MinPts$的簇C是$D$的非空子集，它满足以下条件：

1. $\forall p,q$，如果$p\in C$，而且点$q$由点$p$密度可达，那么点$q$也属于簇C（极大性）；
2. $\forall p,q\in C$：$p$和点$q$是密度相连的（连接性）。

定义7：（噪声点）设$C_1,C_2,...,C_k$是样本集$D$的所有的簇，那么噪声点就是数据集$D$中，不属于以上所有簇的样本点。即
$$\text{noise}=\{p\in D|\forall i:p\notin C_i\},i=1,2,...,k$$

引理1：设点$p$是样本集$D$中的样本点，而且$\left|N_{Eps}(p)\right|\ge MinPts$，即点$p$是核心点，那么集合$O=\{o|o\in D,且o由p密度可达\}$是一个簇。
簇$C$中的每一个点有$C$种的任意一个核心点密度可达的，所以簇$C$刚好包含了所有由它的核心点密度可达的点。

引理2：设$C$是一个簇，$p$是簇$C$中的任意一点且$\left|N_{Eps}(p)\right|\ge MinPts$，那么$C$等价于集合$O$，其中
$$O=\{o|o\in D,且o由p密度可达\}$$

2.2 算法实现步骤

输入：样本集$D=\{x_1,x_2,...,x_m\}$，邻域参数（$Eps$，$MinPts$）

输出：簇的划分$C=\{C_1,C_2,...,C_k\}$

1） 初始化核心点集$\Omega =\varnothing$ ，初始化聚类簇的序号$k=0$ ，初始化未访问的样本点集$\Gamma =D$ ，簇的划分$C=\varnothing$

2） 对于$j=1,2,...,m$，按照下列步骤找出所有的核心点：

• 通过距离度量的方式，找到样本点$x_j$的Eps-邻域 $N_{Eps}(x_j)$
• 如果Eps-邻域 的点数$\left|N_{Eps}(p)\right|\ge MinPts$，则将$x_j$加入到核心点集$\Omega$中：$\Omega =\Omega \cup \{x_j\}$

3） 如果核心点集$\Omega =\varnothing$ ，则算法结束，否则转入步骤4）

4）在核心点集$\Omega$中，随机选择一个核心点$o$，初始化当前簇的核心点队列${\Omega }_{cur}=o$，更新类别序号$k=k+1$，初始化当前簇样本集合$C_k=\{o\}$，更新未访问样本集合$\Gamma =\Gamma -\{o\}$

5）如果当前簇的核心点队列${\Omega }_{cur}=\varnothing$，则当前聚类簇$C_k$生成完毕，更新簇的划分$C=\{C_1,C_2,...,C_k\}$，更新核心点集$\Omega =\Omega -C_k$，转入步骤3）

6）在当前簇的核心点队列${\Omega }_{cur}$中随机取出一个核心点$o^{{}^{\prime }}$，通过邻域距离阈值$Eps$划出所有Eps-邻域 $N_{Eps}(o^{{}^{\prime }})$，令$\Delta =N_{Eps}(o^{{}^{\prime }})\cap \Gamma$，更新当前簇的样本集合$C_k=C_k\cup \Delta$，更新未访问样本集合$\Gamma =\Gamma -\Delta$，更新核心点队列${\Omega }_{cur}={\Omega }_{cur}\cup (\Delta \cap \Omega )-o^{{}^{\prime }}$，转入步骤5）

最终程序执行完成后将输出簇的划分结果$C=\{C_1,C_2,...,C_k\}$。

---

3 伪代码

根据以上算法，写出如下伪代码的形式：

其中ExpandCluster函数的伪代码形式如下：

---

4 实验结果

利用 SEQUOIA 2000 的部分测试样本，测试DBSCAN算法以及CLARANS算法的聚类效果，并做对比。
以下是CLARANS算法的聚类结果：

以下是DBSCAN的聚类结果：

由实验结果可以看出，DBSCAN对任意形状的样本集都具有较好的更符合人类直观的聚类效果，并在聚类的同时可以找出噪声点并排除噪声点。

下表展示了DBSCAN算法与CLARANS算法的聚类效率的对比（单位 秒）：

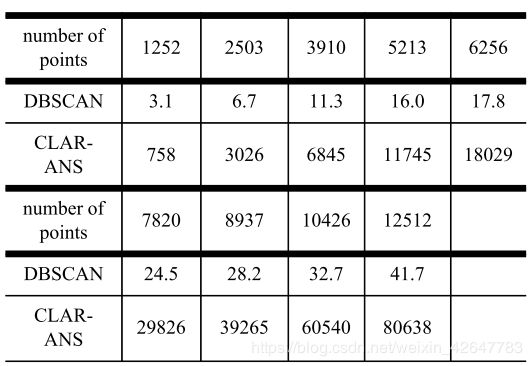
由表可以看出，DBSCAN的聚类效率更高，比CLARANS能快出1到2个数量级。

---

5 优缺点

DBSCAN具有以下优点：

• 可以对任意形状的稠密数据集进行聚类；
• 可以在聚类的同时发现异常点，对数据集中的异常点不敏感；
• 相对于K-Means等聚类方法，DBSCAN对结果没有偏倚，其初始值的设置几乎不会影响聚类结果

DBSCAN也有它的缺点：

• 如果样本集的密度不均匀、聚类间距差相差很大时，聚类质量较差，这时用DBSCAN聚类一般不适合；
• 如果样本集较大时，聚类收敛时间较长，此时可以对搜索最近邻时建立的KD树或者球树进行规模限制来改进；
• 调参相对于传统的K-Means之类的聚类算法较为复杂，主要需要对距离阈值$Eps$和邻域样本数阈值$MinPts$联合调参，不同的参数组合对最后的聚类效果有较大影响。

---

6 小结

和传统的K-Means算法相比，DBSCAN最大的不同就是不需要输入类别数$k$，当然它最大的优势是可以发现任意形状的聚类簇，也就是说它可以用于非凸数据集的聚类，而不只是像K-Means等算法仅仅局限于凸样本集的聚类。同时它在聚类的同时还可以找出异常点，这点和BIRCH算法类似。当数据集不是稠密的类型，就不适合采用DBSCAN算法。

---

7 参考文献

[1] Ester, Martin & Kriegel, Hans-Peter & Sander, Joerg & Xu, Xiaowei. (1996). A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise. KDD. 96. 226-231.
[2] DBSCAN密度聚类算法
[3] 聚类分析常用算法原理：KMeans,DBSCAN, 层次聚类

---

原创性声明：本文属于作者原创性文章，小弟码字辛苦，转载还请注明出处。谢谢~

如果有哪些地方表述的不够得体和清晰，有存在的任何问题，欢迎评论和指正，谢谢各路大佬。

有需要相关技术支持的可咨询QQ：297461921