李航统计学习方法(第二版)第二章 感知机学习笔记【实战篇】
感知机学习笔记【实战篇】
- 原始形式
- 对偶形式
原始形式
本节用李航大大第二版统计学习方法中的例题作为例子来进行学习与编码。
题目是这个样子的【和第一版例题一样】
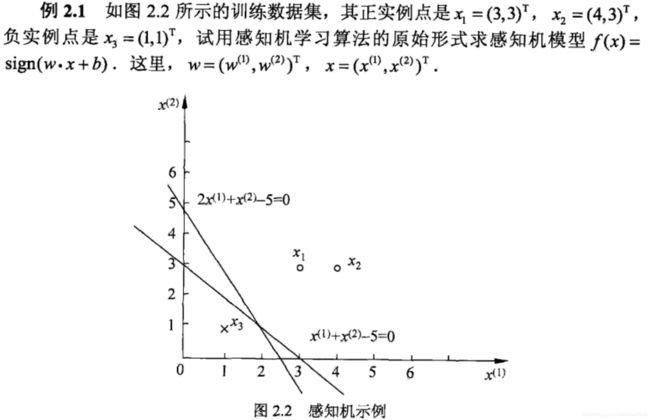
我们回顾一下原始形式时的算法思想:
1)设定 w, b 的初始值
2)随机选取样本空间中的一个点 ( x i , y i ) (x_i,y_i) (xi,yi)
3)如果 y i ∗ ( w ∗ x i + b ) < 0 y_i*(w*x_i+b)<0 yi∗(w∗xi+b)<0:
w ← w + η ∗ x i ∗ y i w \leftarrow w + \eta*x_i*y_i w←w+η∗xi∗yi
b ← b + η ∗ y i b \leftarrow b + \eta*y_i b←b+η∗yi
4)重复步骤2),直至样本空间中没有误分类点为止。
我们将上述思想转化为可读的另一种文字+代码语言:
1)初始化参数:我们这里假设所求参数初始值为0,即 w = ( 0 , 0 ) , b = 0 w=(0,0), b=0 w=(0,0),b=0。
2)样本空间:样本空间为 x 1 = ( 3 , 3 ) T , x 2 = ( 4 , 3 ) T , x 3 = ( 1 , 1 ) T x_1=(3,3)^T, x_2=(4,3)^T,x_3=(1,1)^T x1=(3,3)T,x2=(4,3)T,x3=(1,1)T,对应的目标变量分别为 y 1 = 1 , y 2 = 1 , y 3 = − 1 y_1=1,y_2=1,y_3=-1 y1=1,y2=1,y3=−1。实际上这些样本空间用向量表示可以这么写: x = [ ( 3 , 3 ) , ( 4 , 3 ) , ( 1 , 1 ) ] T , y = [ 1 , 1 , − 1 ] x=[(3,3),(4,3),(1,1)]^T, y=[1,1,-1] x=[(3,3),(4,3),(1,1)]T,y=[1,1,−1]。
判断条件: y i ∗ ( w ∗ x i ) + b y_i*(w*x_i)+b yi∗(w∗xi)+b这里可以表示成直接将 i i i用下标替换就好了。
参数更新:如判断条件一样
我们开始进行代码编写:
import numpy as np
X=[(3,3),(4,3),(1,1)] # 样本特征
y = [1,1,-1] # 样本label
sample_number = len(y) # 样本数量