无训练数据压缩网络《Data-Free Learning of Student Networks》读后总结
无训练数据压缩网络《Data-Free Learning of Student Networks》读后总结
- 前言
- 文章主要内容与贡献
- 提出了一个有效的无数据训练的办法
- 有效的组合了GAN和教师-学生网络
- 设计了适合于这篇文章中的GAN模型的总损失函数$L_{Total}$
- one-hot损失函数$L_{oh}$
- 激活损失函数$L_{a}$
- 生成图像的信息熵损失函数$L_{ie}$
- 利用知识蒸馏将教师网络压缩为学生网络
- 对多个数据集和多个经典网络进行了实验以证明有效性
- 实验一:(MNIST/HintonNet)+LeNet-5
- 实验二:剥离试验(Ablation Experiments)
- 实验三:可视化结果
- 子实验一:生成网络的最终输出结果
- 子实验二:学生网络的特征提取器
- 实验四:CIFAR+ResNet
- 实验五:CelebA+AlexNet
- 实验六:扩展实验
前言
这是一些对于论文《Data-Free Learning of Student Networks》的简单的读后总结,首先先奉上该文章的下载超链接:点击这里下载论文。该文章也附有github源代码:源代码
这篇文章是由北大和华为的人员合作完成的,作者分别是Hanting Chen、Yunhe Wang、 Chang Xu、 Zhaohui Yang、 Chuanjian Liu、 Boxin Shi、Chunjing Xu、Chao Xu、Qi Tian。其利用GAN和教师-学生网络来使得学生网络可以在无训练数据的情况下学习到教师网络的能力,关键之处在于无训练数据。但其实该文章主要研究的是对神经网络的压缩。
文章主要内容与贡献
该文章的贡献为:
- 提出了一个有效的无数据训练的办法;
- 有效的组合了GAN和教师-学生网络;
- 设计了适合于这篇文章中的GAN模型的总损失函数 L T o t a l L_{Total} LTotal;
- 利用知识蒸馏将教师网络压缩为学生网络;
- 对多个数据集和多个经典网络进行了实验以证明有效性。
提出了一个有效的无数据训练的办法
因为文章有华为诺亚方舟实验室的人员参与论文写作,同时该论文也是北大的人在参观华为诺亚方舟实验室时完成的。因此这篇文章有不少商业以及实用的味道。该文章从很多时候难以获取原始训练集的角度出发,提出了一个有效的无数据训练的办法,通过有效的组合了GAN和教师-学生网络来使得学生网络可以有效地学习到教师网络的性能,需要注意的是教师网络的参数量和计算量是大于学生网络的。因此,这篇文章实际上做的是在无训练数据的情况下将教师网络压缩为学生网络,同时尽可能的不降低网络的性能。
有效的组合了GAN和教师-学生网络
这篇文章的网络名称为DAFL(Data-Free Learning),首先先来看一下总体的网络结构:
简单来说,在整个网络体系中,总共有三个网络,其中,GAN中有一个生成网络和一个判别网络,而教师-学生网络中分别是一个教师网络和一个学生网络,GAN和教师-学生网络融合的地方便是判别网络和教师网络是同一个网络。由于终极目标是将教师网络压缩为学生网络,因此不管是在GAN中还是教师-学生网络中教师网络(判别网络)都是不变的,不对其进行任何更改或参数更新。
网络运行的框架如下所示:

网络的运行流程(循环直到收敛)为:
- 进行一次GAN的训练,但此次训练中仅更新生成网络;
- 此时,生成网络生成一组数据,分别将这些数据输入教师网络和学生网络,然后通过知识蒸馏( knowledge distillation,KD)的方法来对学生网络的参数进行更新。
设计了适合于这篇文章中的GAN模型的总损失函数 L T o t a l L_{Total} LTotal
由于判别网络用的是已被训练好的网络,但是该网络被训练来做的是图像分类任务而不是去分辨图像是真实的还是生成的。因此,需要对损失函数进行调整才能使得GAN可以得以进行。
该论文将损失函数分为了三个部分:
![]()
分别是 L o h L_{oh} Loh、 L a L_{a} La和 L i e L_{ie} Lie,其中 α \alpha α和 β \beta β是固定的数值参数,用来调整 L o h L_{oh} Loh、 L a L_{a} La和 L i e L_{ie} Lie各自所占的比例的。
one-hot损失函数 L o h L_{oh} Loh
首先来看one-hot损失函数 L o h L_{oh} Loh:

其中, H c r o s s H_{cross} Hcross是交叉熵损失函数,有 i i i个样本, y T i y^i_T yTi是判别网络(教师网络)对第 i i i个样本的输出,因为判别网络(教师网络)是对图像进行分类的网络,因此其有多个输出并使用的是softmax,因此当输入的是真实的图像时,此时输出应该是稀疏的,即应该有某个类别的概率是非常大的,而如果输入的图像和训练集图像差异太大的话,此时网络是无法提取有用的特征来作最后的分类的,此时判别网络(教师网络)的输出就不是稀疏的。因此,通过判断判别网络(教师网络)输出的稀疏性与否可以来衡量输入是生成网络生成的还是真实的。
激活损失函数 L a L_{a} La
其次是激活损失函数 L a L_{a} La:
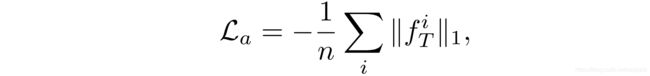
其中, ∥ ⋅ ∥ 1 \|\cdot\|_1 ∥⋅∥1是传统的 l 1 l_1 l1范数, l 1 l_1 l1范数的主要作用是为了获得稀疏性,在此处相当于想让 f T i f^i_T fTi尽可能多的被激活,因此加上负号的意思就是让它们尽量的不稀疏, l 1 l_1 l1范数在此处也被称为稀疏正则化。 f T i f^i_T fTi是教师网络提取第 i i i个图像的最终的特征,即第一个全连接层的输入。 L a L_{a} La相当于是看输入的图像是否会触发网络的某些特征提取器,如果能触发,则证明输入的图片和真实训练集是比较相似的,如果触发的特征提取器较多,则说明输入的图片是真实图片的概率较大,因为网络中的特征提取器就是被训练来提取真实训练集中的图像特征的。这样便能分辨输入的图像时自然的还是生成的了。
生成图像的信息熵损失函数 L i e L_{ie} Lie
最后来看看生成图像的信息熵损失函数 L i e L_{ie} Lie:
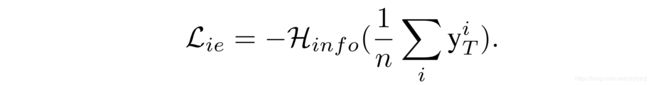
因为通常来说训练集中的每个类别的样本数应该都是相同的,例如MNIST数据集中,总共有60000个训练样本和10个类别,其中每个类别都有6000张图片。所以根据这个先验信息,作者提出了这个信息熵损失函数 L i e L_{ie} Lie,每个类生成的图像的频率分布为 1 n ∑ i y T i \dfrac 1n \sum\limits_iy^i_T n1i∑yTi, y T i y^i_T yTi是教师网络对第 i i i个输出图像的输出,当损失最小时,向量 1 n ∑ i y T i \dfrac 1n \sum\limits_iy^i_T n1i∑yTi中的每一个元素都等于 1 k \dfrac 1k k1。这意味着生成网络 G G G可以大致相同的概率生成每个类别的图像。因此,最小化所生成的图像的信息熵可以得到一组类别数量均衡的合成图像。
现在来解释一下 H i n f o H_{info} Hinfo,给定一组概率向量 p = ( p 1 , p 2 , … , p k ) p=(p_1,p_2,\dots,p_k) p=(p1,p2,…,pk),测量 p p p的混淆程度的信息熵计算的计算方式为: H i n f o ( p ) = 1 k ∑ i p i log ( p i ) H_{info}(p)=\dfrac 1k \sum\limits_ip_i\log(p_i) Hinfo(p)=k1i∑pilog(pi), H i n f o ( p ) H_{info}(p) Hinfo(p)的值表示 p p p拥有的信息量,当所有变量等于 1 k \dfrac 1k k1时,信息量将达到最大值。
其实,信息熵损失函数 L i e L_{ie} Lie的主要功能就是想让生成网络学习到去生成每个类别分布一致的数据。
此处取负号的原因是 H i n f o ( 1 n ∑ i y T i ) H_{info}(\dfrac 1n \sum\limits_iy^i_T) Hinfo(n1i∑yTi)的值域是 [ 0 , 1 ] [0,1] [0,1]。
利用知识蒸馏将教师网络压缩为学生网络
知识蒸馏(Knowledge Distillation, KD)
Geoffrey Hinton, Oriol Vinyals, and Jeff Dean. Distilling the knowledge in a neural network. arXiv preprint
arXiv:1503.02531, 2015. 1, 2, 3, 5, 7, 8
是一种广泛使用的方法,用于将输出信息从大的网络转移到较小的网络,以获得更高的性能,它不使用给定网络的参数和体系结构。
通过以下的损失函数 L K D L_{KD} LKD即可实现将教师网络的知识蒸馏到学生网络的操作:
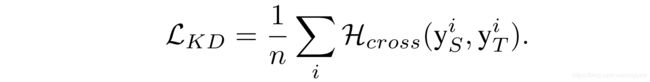
其中, H c r o s s H_{cross} Hcross是交叉熵损失函数, y S i y^i_S ySi是学生网络对第 i i i个输出图像的输出, y T i y^i_T yTi是教师网络对第 i i i个输出图像的输出,此处主要就是来想使得学生网络的输出尽可能的贴近教师网络的输出。因此,利用知识转移技术,可以在不需要特定网络结构的情况下对学生网络进行优化。
对多个数据集和多个经典网络进行了实验以证明有效性
实验一:(MNIST/HintonNet)+LeNet-5
第一个实验是在MNIST数据集上来完成的。其中,第一个子实验为教师网络为LeNet-5,学生网络为LeNet-5-Hafl(修改后的版本为每层通道数的一半);第二个子实验为教师网络由两个有1200个单元的隐藏层组成(Hinton-784-1200-1200-10),学生网络由两个有800个单元的隐藏层组成(Hinton-784-800-800-10)。实验结果如下所示:
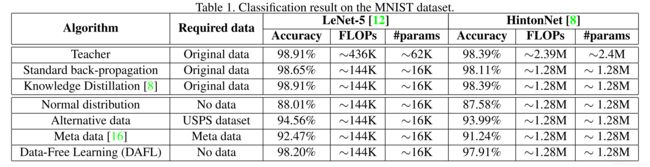
由上表可知,在使用LeNet-5时,学生网络所需的计算量(FLOPs)仅为教师网络的 1 3 \dfrac 13 31,参数数量仅为教师网络的 1 4 \dfrac 14 41。
在有原始数据的情况下,LeNet-5的精度为 98.91 % 98.91\% 98.91%,LeNet-5-Hafl的精度为 98.65 % 98.65\% 98.65%,而经过知识蒸馏的LeNet-5-HALF的精度为 98.91 % 98.91\% 98.91%,和教师网络一样,这证明了知识蒸馏的有效性,在网络更小的情况下可以通过知识蒸馏获得和大网络一样的性能。
在没有原始数据的情况下,使用随机生成的正态分布数据来作为训练集时,LeNet-5-Hafl的精度为 88.01 % 88.01\% 88.01%,这说明了没有训练集时,使用随机数据虽然也能获得一定的效果但是效果较差。使用USPS数据集(和MNIST数据集类似的数据集)来作为训练集,测试集是MNIST数据集时,LeNet-5-Hafl的精度为 94.56 % 94.56\% 94.56%,这说明了就算是类似的数据集直接迁移过来的效果也不是很好。使用元数据(Meta data,即各层激活的均值和标准差)来作为训练集,测试集是MNIST数据集时,LeNet-5-Hafl的精度为 92.47 % 92.47\% 92.47%,其效果差于使用相似数据集USPS的训练效果。最后就是该文章的DAFL方法,其在无训练数据的情况下,使得LeNet-5-Hafl的精度为 98.20 % 98.20\% 98.20%,仅比LeNet-5的精度少 0.71 % 0.71\% 0.71%。
第二种结构,HintonNet的实验结果与LeNet-5的实验结果类似。
实验二:剥离试验(Ablation Experiments)
这个实验的目的是看看该文章提出的每个部分是否都是缺一不可的,如果少了某一部分,性能是否会变差以及会变差多少,实验结果如下表所示:

上表处打√的部分即是使用了该损失函数的标志,例如第四列处,即仅使用了信息交叉熵损失函数。由上表可知,每个损失函数都可以提高DAFL的性能,其中,最有用的是第二行的信息交叉熵损失函数,其次是第一行的one-hot损失函数,最后是第三行的特征图激活函数。
实验三:可视化结果
子实验一:生成网络的最终输出结果
生成网络的最终输出结果图如下所示:

图(a)是原始的MNIST的一些图像,从0到9都有,图(b)则是生成网络生成的图像,这些图像是判别网络判别的从0到9的数,可以看见还是有几个数是依稀可辨的,这说明了该文章设计的GAN的有效性。
子实验二:学生网络的特征提取器
在MNIST数据集上学习的第一卷积层中过滤器的可视化结果如下所示:

其中,图(a)是教师网络的在MNIST数据集上学习的第一卷积层中过滤器的可视化结果,图(b)是学生网络在MNIST数据集上学习的第一卷积层中过滤器的可视化结果,可以看见学生网络有效的学到了第1、4、5、6个过滤器。
实验四:CIFAR+ResNet
第四个实验是在CIFAR数据集上来完成的。其中,教师网络为ResNet-34,学生网络为ResNet-18。实验结果如下所示:
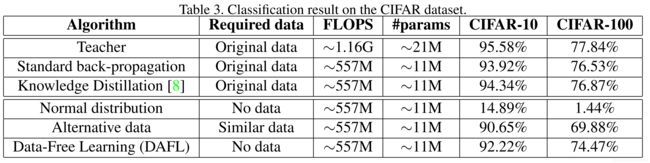
从表中可以看出,学生网络ResNet-18的计算量和参数数量仅为教师网络ResNet-34的一半。由于CIFAR数据集的复杂度远大于MNIST,因此ResNet-18的准确率要比ResNet-34低不少,就算经过知识蒸馏,还是要低 1 % 1\% 1%左右的准确率。在无数据仅使用随机生成数据来作为输入的情况下,ResNet-18的效果极差。在使用相似的数据集进行训练时,直接迁移到越复杂的数据集的效果就越差,但DAFL可以做得远好于前两者的效果,可以获得接近于有原始数据时的训练效果。
实验五:CelebA+AlexNet
实验五是在CelebA数据集上做的实验,教师网络为AlexNet,学生网络为AlexNet-Hafl(修改后的版本为每层通道数的一半),实验结果如下所示:
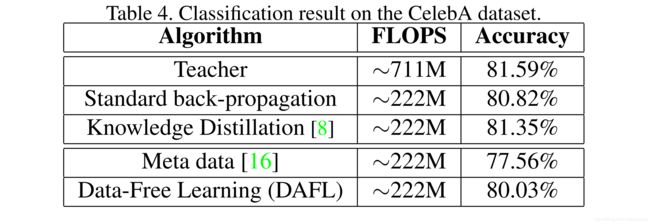
AlexNet-Hafl的计算量仅为AlexNet的 30 % 30\% 30%,由于缩小了网络,因此AlexNet-Hafl的准确率比AlexNet略低,但经过知识蒸馏后可以非常接近于AlexNet的准确率。此处,DAFL的效果最终也能有合适的效果,但此处没有将使用相似数据集的结果放上来,有可能是因为那个结果比DAFL的好。
实验六:扩展实验
最后一个实验是假设教师网络的结构和学生网络一致时,学生网络的性能:

从此处可以看出,学生网络的性能皆比小网络时有所上升。