ensemble learning集成学习
在实际的学习任务中,得到强学习器要比得到弱学习器困难的多。于是就有人研究如何将弱学习器组合成强学习器(毕竟三个臭皮匠赛过诸葛亮,结合集体的智慧得到好的结果),一般将这一类的方法统称为集成学习。集成学习会要求基学习器“好而不同”。“好”是指每个基学习器要有一定的辨别能力,至少要强于随机猜测;“不同”是指多个基学习器之间要具有一定的差异性(各有所长)。下面的思维导图对集成学习的知识进行了归纳(主要参见周志华老师的西瓜书)。
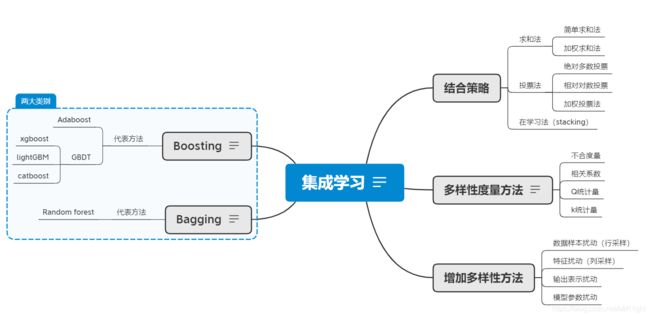
上图右侧解答了三个问题:
- 如何衡量两个弱学习器之间的相似度
- 如何增加弱学习器的多样性
- 如何组合使用多个弱学习器
左侧按照基学习器学习方式的不同分为两大类:Boosting和Bagging。
1 Boosting和Bagging
基学习器之间是否有强依赖关系分为Boosting和Bagging。Boosting是基学习器之间存在强依赖关系,必须串行学习每个基学习器。Bagging是基学习器之间不存在强依赖关系,可以并行学习各个基学习器。
1.1Boosting
Boosting方法根据之前模型学习的结果调整样本的分布,简单来说就是增加之前基学习器学习不好样本的权重;降低之前模型已经学会了的样本权重。
Boosting方法一般是加法模型。不断增加一个新基学习器来降低损失。将模型和损失分别用以下公式表示:
G ( x ) = ∑ t = 1 T f t ( x ) L = ∑ i = 1 m l ( y i , G ( x i ) ) G(x)=\sum_{t=1}^Tf_t(x)\\L=\sum_{i=1}^ml(y_i,G(x_i)) G(x)=t=1∑Tft(x)L=i=1∑ml(yi,G(xi))
其中,T表示基学习器的个数,m表示样本个数。
在第t轮迭代时,前t-i个基学习器 f 1 ( x ) , f 2 ( x ) , . . . , f t − 1 ( x ) f_1(x),f_2(x),...,f_{t-1}(x) f1(x),f2(x),...,ft−1(x)是已知的。需要求的是 f t ( x ) f_t(x) ft(x)。第t轮的损失函数可表示为:
L t = ∑ i = 1 m l ( y i , G t − 1 ( x i ) + f t ( x i ) ) L^t=\sum_{i=1}^ml(y_i,G_{t-1}(x_i)+f_t(x_i)) Lt=i=1∑ml(yi,Gt−1(xi)+ft(xi))
在每一轮迭代中直接优化这个损失函数是困难的。一般有两种方式简化优化问题:
- 巧妙的设计损失函数,简化当前的优化目标
- 梯度提升,损失L对 G t − 1 ( x ) G_{t-1}(x) Gt−1(x)的负梯度作为当前模型的学习目标
1.1.1巧妙的损失函数设计
Adaboost的指数损失和提升树中的MSE损失就是按照这一思想设计的基学习器学习算法。
(1)Adaboost的指数损失
Adaboost模型是用于二分类问题的加法模型,损失是指数损失函数。通过推导发现,在每一轮的优化中,优化当前的损失函数,等价于不断调整样本分布并优化0-1损失函数。具体推导在Adaboost博文中有介绍。
(2)提升树的MSE损失
提升树是以决策树(CART二叉树)为基学习器的提升方法。当损失函数是MSE损失时。每一轮的迭代区最小化损失函数等价于学习label和当前预测结果的残差。
推导:当前模型为树的加法模型,损失函数为欧氏距离。
G ( x ) = ∑ t = 1 T f t ( x ) L = ∑ i = 1 m ( y i − y i ^ ) 2 G(x)=\sum_{t=1}^Tf_t(x)\\L=\sum_{i=1}^m(y_i-\hat{y_i})^2 G(x)=t=1∑Tft(x)L=i=1∑m(yi−yi^)2
其中每一个 f t ( x ) f_t(x) ft(x)都表示一颗二叉回归树。
在第t轮迭代时, G t − 1 ( x ) G_{t-1}(x) Gt−1(x)是已知的。当前的损失函数为:
L t = ∑ i = 1 m l ( y i , y i ^ ( t − 1 ) + f t ( x ) ) = ∑ i = 1 m ( y i − y i ^ ( t − 1 ) + f t ( x ) ) 2 = ∑ i = 1 m ( ( y i − y i ^ ( t − 1 ) ) + f t ( x ) ) 2 = ∑ i = 1 m l ( y i − y i ^ ( t − 1 ) , f t ( x ) ) L^t=\sum_{i=1}^ml(y_i,\hat{y_i}^{(t-1)}+f_t(x))\\=\sum_{i=1}^m(y_i-\hat{y_i}^{(t-1)}+f_t(x))^2\\=\sum_{i=1}^m((y_i-\hat{y_i}^{(t-1)})+f_t(x))^2\\=\sum_{i=1}^ml(y_i-\hat{y_i}^{(t-1)},f_t(x)) Lt=i=1∑ml(yi,yi^(t−1)+ft(x))=i=1∑m(yi−yi^(t−1)+ft(x))2=i=1∑m((yi−yi^(t−1))+ft(x))2=i=1∑ml(yi−yi^(t−1),ft(x))
y i − y i ^ ( t − 1 ) y_i-\hat{y_i}^{(t-1)} yi−yi^(t−1)即为残差。当前的学习目标就是拟合残差。
1.1.2梯度提升
(这部分参考知乎关于梯度提升的回答)
上面使用的损失函数,巧妙的简化了当前要优化的任务。当使用其他的损失函数,或者在损失中增加正则项时。可以使用梯度提升来简化当前的学习目标。当前 f t ( x ) f_t(x) ft(x)拟合loss对 G t − 1 ( x ) G_{t-1}(x) Gt−1(x)的负梯度。
梯度提升和用于优化算法的梯度下降思想是一样的。都是用于在迭代中求最优解。区别就在于梯度下降是对于参数 θ \theta θ来说的,在迭代中不断的加上负的梯度值,逐渐逼近极值点。梯度提升是对于函数 f t ( x ) f_t(x) ft(x)来说的,每一轮迭代中 f t ( x ) f_t(x) ft(x)去拟合loss对于 G t − 1 ( x ) G_{t-1}(x) Gt−1(x)的负梯度。
| 算法 | 空间 | 优化公式 | 损失函数 |
|---|---|---|---|
| 梯度下降 | 参数空间 | θ t = θ t − 1 + Δ θ \theta_t=\theta_{t-1}+\Delta\theta θt=θt−1+Δθ | L = ∑ i l ( y i , f ( θ t ) ) L=\sum_{i}l(y_i,f(\theta_t)) L=∑il(yi,f(θt)) |
| 梯度提升 | 假设空间 | G t = G t − 1 + Δ G G_t=G_{t-1}+\Delta G Gt=Gt−1+ΔG | L = ∑ i l ( y i , G t ( x i ) ) L=\sum_il(y_i,G_t(xi)) L=∑il(yi,Gt(xi)) |
使用梯度提升方式优化的提升树称为GBDT(Gradient boosting descision tree)。Xgboost是GBDT的一种高效实现方式,参见另一篇博客。
1.2 Bagging
Bagging使用有放回的采样,每次采样一个样本,重复m次得到包含m个样本的样本集。再将上面操作重复T次得到T个包含m个样本的集合。通过样本扰动(行采样)增加基学习器的多样性。Bagging方法就是使用一些扰动方式得到多个“不同”的基分类器。然后使用投票法决策。
Bagging的基学习器学习方式和正常分类器的算法很相似。不多做介绍。Bagging的代表方式是随机森林(Random forest)。
1.2.1 Random forest
随机森林进行样本扰动(行采样)的同时,在决策树的特征选择时使用了特征扰动(列采样)。具体来说,传统决策树划分选择最优属性时,从当前结点的属性集合(假设有d个)中根据选择规则选择一个最优属性;而在RF中,对于每个基决策树的每个结点,先从该结点的属性集合中随机选择一个包含k个特征的子集。在从k个特征集合中选择最优特征作为划分属性。当k=d时,RF基决策树的构建与传统决策性相同;当k=1时,随机选择一个属性作为划分属性。一般选择k=log(d)。
参考
[1]周志华,机器学习
[2]知乎https://zhuanlan.zhihu.com/p/86354141