卷积神经网络之VGG(2014)

VGG(2014)

文档存放更新地址：https://github.com/lartpang/ML_markdown

文章书写匆忙，有些使用了网上其他朋友的文字以及图片，但是没有及时复制对应的链接，在此深表歉意，以及深深的感谢。
如有朋友看到了对应的出处，或者作者发现，可以留言，小弟马上修改，添加引用。

前言

2014年是个绽放年，出了两篇重要的论文：VGG、GoogLeNet。

来自牛津大学的VGG网络是第一个在每个卷积层使用更小的3×3卷积核对图像进行卷积，并把这些小的卷积核排列起来作为一个卷积序列。通俗点来讲就是对原始图像进行3×3卷积，然后再进行3×3卷积，连续使用小的卷积核对图像进行多次卷积。

或许很多人看到这里也很困惑为什么使用那么小的卷积核对图像进行卷积，并且还是使用连续的小卷积核？VGG一开始提出的时候刚好与LeNet的设计原则相违背，因为LeNet相信大的卷积核能够捕获图像当中相似的特征（权值共享）。AlexNet在浅层网络开始的时候也是使用9×9、11×11卷积核，并且尽量在浅层网络的时候避免使用1×1的卷积核。但是VGG的神奇之处就是在于使用多个3×3卷积核可以模仿较大卷积核那样对图像进行局部感知。后来多个小的卷积核串联这一思想被GoogleNet和ResNet等吸收。

VGG相信如果使用大的卷积核将会造成很大的时间浪费，减少的卷积核能够减少参数，节省运算开销。虽然训练的时间变长了，但是总体来说预测的时间和参数都是减少的了。

概要

卷积网络（ConvNets）近来在大规模图像和视频识别方面取得了巨大成功（Krizhevsky等，2012；Zeiler＆Fergus，2013；Sermanet等，2014；Simonyan＆Zisserman，2014）由于大的公开图像存储库，例如ImageNet，以及高性能计算系统的出现，例如GPU或大规模分布式集群（Dean等，2012），使这成为可能。特别是，在深度视觉识别架构的进步中，ImageNet大型视觉识别挑战（ILSVRC）（Russakovsky等，2014）发挥了重要作用，它已经成为几代大规模图像分类系统的测试台，从高维度浅层特征编码（Perronnin等，2010）（ILSVRC-2011的获胜者）到深层ConvNets（Krizhevsky等，2012）（ILSVRC-2012的获奖者）。

随着ConvNets在计算机视觉领域越来越商品化，为了达到更好的准确性，已经进行了许多尝试来改进Krizhevsky等人（2012）最初的架构。例如，ILSVRC-2013（Zeiler＆Fergus，2013；Sermanet等，2014）表现最佳的提交使用了更小的感受窗口尺寸和更小的第一卷积层步长。另一条改进措施在整个图像和多个尺度上对网络进行密集地训练和测试（Sermanet等，2014；Howard，2014）。

在本文中，我们解决了ConvNet架构设计的另一个重要方面——其深度。为此，我们修正了架构的其它参数，并通过添加更多的卷积层来稳定地增加网络的深度，这是可行的，因为在所有层中使用非常小的（3×3）卷积滤波器。

新意

我们的主要贡献是使用非常小的（3×3）卷积滤波器架构对网络深度的增加进行了全面评估，这表明通过将深度推到16-19加权层可以实现对现有技术配置的显著改进。

两个3×3卷积层堆叠（没有空间池化）有5×5的有效感受野；三个这样的层具有7×7的有效感受野。

那么我们获得了什么？例如通过使用三个3×3卷积层的堆叠来替换单个7×7层。

• 首先，我们结合了三个非线性修正层，而不是单一的，这使得决策函数更具判别性。
• 其次，我们减少参数的数量：假设三层3×3卷积堆叠的输入和输出有C个通道，堆叠卷积层的参数为$3\ast (3^2{C}^2)=27C^2$个权重；同时，单个7×7卷积层将需要$7^2{C}^2=49C^2$个参数，即参数多81％。

这可以看作是对7×7卷积滤波器进行正则化(减少了参数)，迫使它们通过3×3滤波器（在它们之间注入非线性）进行分解。

架构

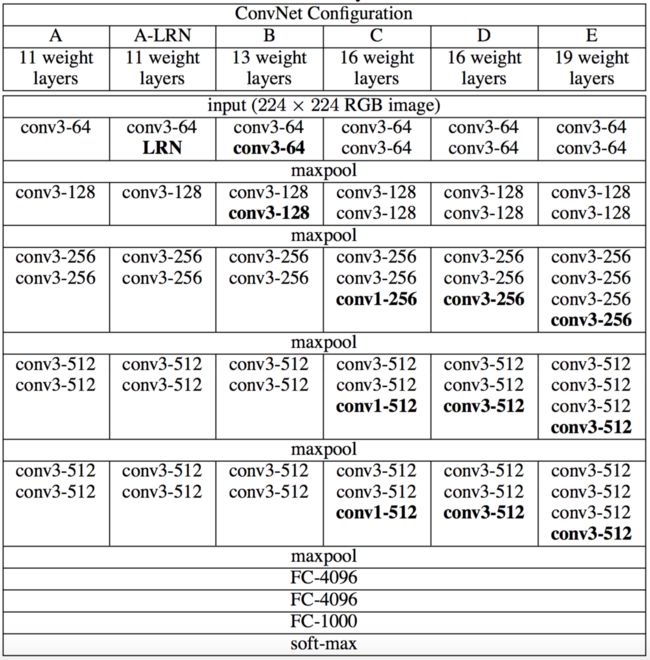
ConvNet配置（以列显示）。随着更多的层被添加，配置的深度从左（A）增加到右（E）（添加的层以粗体显示）。卷积层参数表示为“conv⟨感受野大小⟩-通道数⟩”。为了简洁起见，不显示ReLU激活功能。

我们报告了每个配置的参数数量。尽管深度很大，我们的网络中权重数量并不大于具有更大卷积层宽度和感受野的较浅网络中的权重数量（144M的权重在（Sermanet等人，2014）中）。

参数数量（百万级别）:

训练

1. 预处理:

   • 在训练期间，我们的ConvNet的输入是固定大小的224×224 RGB图像。

     令S是等轴归一化的训练图像的最小边，ConvNet输入从S中裁剪（我们也将S称为训练尺度）。虽然裁剪尺寸固定为224×224，但原则上S可以是不小于224的任何值：

     • 对于S=224，裁剪图像将捕获整个图像的统计数据，完全扩展训练图像的最小边；
     • 对于S»224，裁剪图像将对应于图像的一小部分，包含小对象或对象的一部分。在每一次随机梯度下降迭代中都在归一化后的图片上随机裁剪一个224×224的方块作为训练的输入。

     此外，由于数据集中的图像大小是不一致的，所以需要通过缩放将其变为想要的尺寸S×S。对于尺寸，文中有两种处理方式来设置训练尺度S。

     • 第一种是修正对应单尺度训练的S（注意，采样裁剪图像中的图像内容仍然可以表示多尺度图像统计）。在我们的实验中，我们评估了以两个固定尺度训练的模型. 256/384.当S=384时，训练集太大导致训练时间大大增加，为了减少训练时间，加快训练过程，作者直接使用S=256的训练的结果来初始化S=384的参数，并设置较小的学习率10e-3。

     • 第二种是多尺度训练，其中每个训练图像通过从一定范围[Smin，Smax]（我们使用Smin=256和Smax=512）随机采样S来单独进行归一化。由于图像中的目标可能具有不同的大小，因此在训练期间考虑到这一点是有益的。这也可以看作是通过尺度抖动进行训练集增强，其中单个模型被训练在一定尺度范围内识别对象。

       为了速度的原因，我们通过对具有相同配置的单尺度模型的所有层进行微调，训练了多尺度模型，并用固定的S=384进行预训练。

   • 我们唯一的预处理是从每个像素中减去在训练集上计算的RGB均值。

2. 优化手段

   • 使用具有动量的小批量梯度下降（基于反向传播（LeCun等人，1989））优化多项式逻辑回归目标函数来进行训练。批量大小设为256，动量为0.9。

   • 学习率初始设定为$10^{-2}$，然后当验证集准确率停止改善时，减少10倍。学习率总共降低3次，学习在37万次迭代后停止（74个epochs）。

     我们推测，尽管与（Krizhevsky等，2012）相比我们的网络参数更多，网络的深度更大，但网络需要更小的epoch就可以收敛，这是由于

     • 由更大的深度和更小的卷积滤波器尺寸引起的隐式正则化
     • 某些层的预初始化。

     值得注意的是，在提交论文之后，我们发现可以通过使用**Glorot＆Bengio（2010）**的随机初始化程序来初始化权重而不进行预训练。

3. 正则化

   • 训练通过权重衰减（L2惩罚乘子设定为$5\ast 10^{-4}$）进行正则化.
   • 前两个全连接层执行Dropout正则化（丢弃率设定为0.5）

测试

预处理

在测试时，给出训练的ConvNet和输入图像，它按以下方式分类。

• 首先，将其等轴地归一化到预定义的最小图像边，表示为Q（我们也将其称为测试尺度）。

  我们注意到，Q不一定等于训练尺度S.

  缩放后的尺寸为Q×Q大小的图像，Q与S基本无关，文中指出在测试过程中使用了多个Q进行测试，结果取平均。。

• 我们还通过水平翻转图像来增强测试集, 将原始图像和翻转图像的softmax类后验进行平均，以获得图像的最终分数。

细节

• 由于全卷积网络被应用在整个图像上，所以不需要在测试时对采样多个裁剪图像（Krizhevsky等，2012），因为它需要网络重新计算每个裁剪图像，这样效率较低。

  测试方法首先将网络转化为全卷积网络，第一个全连接层转为7×7的卷积层，后两个全连接层转化为1×1的卷积层。结果得到的是一个N×N×M的结果，称其为类别分数图，其中M等于类别个数，N的大小取决于输入图像尺寸Q，计算每个类别的最终得分时，将N×N上的值求平均，此时得到1×1×M的结果，此结果即为最终类别分数，这种方法文中称为密集评估。

• 同时，如Szegedy等人（2014）所做的那样，使用大量的裁剪图像可以提高准确度，因为与全卷积网络相比，它使输入图像的采样更精细。

• 此外，由于不同的卷积边界条件，多裁剪图像评估是密集评估的补充：当将ConvNet应用于裁剪图像时，卷积特征图用零填充，而在密集评估的情况下，相同裁剪图像的填充自然会来自于图像的相邻部分（由于卷积和空间池化），这大大增加了整个网络的感受野，因此捕获了更多的上下文。

• 虽然我们认为在实践中，多裁剪图像的计算时间增加并不足以证明准确性的潜在收益，但作为参考，我们还在每个尺度使用50个裁剪图像（5×5规则网格，2次翻转）评估了我们的网络，在3个尺度上总共150个裁剪图像，与Szegedy等人(2014)在4个尺度上使用的144个裁剪图像。

  这种测试方法，和训练过程类似，不用将网络转化为全卷积网络，是从Q×Q大小的图中随机裁剪224×224的图作为输入，文中裁剪了50个图像，而每个图像之前缩放为三个尺寸，所以每个图像的测试图像数目变为150个，最终结果就是在150个结果中取平均。但是作者指出，该方法效率低下，并且不能证明比第一种方法效果好。

  除此之外，本文还采取了全卷机网络和随机裁剪相结合的方法，即两者结果取平均。其能大大增加网络的感受野，因此捕获更多的上下文信息，实验中也发现这种方法表现最好。

  https://www.jianshu.com/p/692a8d1a6b76

评估

• 单尺度评估(固定尺度测试)

  测试图像大小设置如下：对于固定S的Q=S，对于抖动S∈[Smin,Smax]，Q=0.5(Smin+Smax)。

  

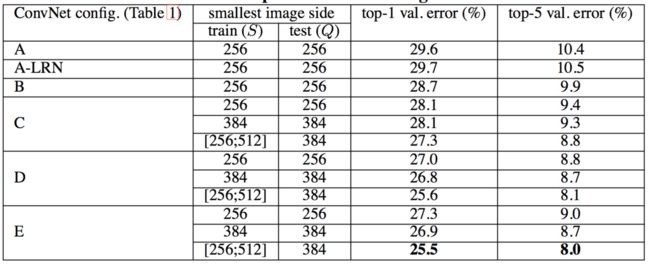
  • 结果可以反映出来, LRN对于模型改善并没有太大效果.在较深的架构中就不再使用.

  • 值得注意的是，尽管深度相同，配置C（包含三个1×1卷积层）比在整个网络层中使用3×3卷积的配置D更差。这表明，虽然额外的非线性确实有帮助（C优于B），但也可以通过使用具有非平凡感受野（D比C好）的卷积滤波器来捕获空间上下文。

  • 我们还将网络B与具有5×5卷积层的浅层网络进行了比较，浅层网络可以通过用单个5×5卷积层替换B中每对3×3卷积层得到（其具有相同的感受野如第2.3节所述）。测量的浅层网络top-1错误率比网络B的top-1错误率（在中心裁剪图像上）高7％，这证实了具有小滤波器的深层网络优于具有较大滤波器的浅层网络。

  • 训练时的尺度抖动（S∈[256;512]）得到了与固定最小边（S=256或S=384）的图像训练相比更好的结果，即使在测试时使用单尺度。这证实了通过尺度抖动进行的训练集增强确实有助于捕获多尺度图像统计.

• 多尺度(多尺度测试)

  在单尺度上评估ConvNet模型后，我们现在评估测试时尺度抖动的影响。它包括在一张测试图像的几个归一化版本上运行模型（对应于不同的Q值），然后**对所得到的类别后验进行平均**。

  • 考虑到训练和测试尺度之间的巨大差异会导致性能下降，用固定S训练的模型在三个测试图像尺度上进行了评估，接近于训练一次：$Q=S-32,S,S+32$。
  • 同时，训练时的尺度抖动允许网络在测试时应用于更广的尺度范围，所以用变量$S\in [Smin;Smax]$训练的模型在更大的尺寸范围$Q=\{S_{min},0.5(S_{min}+S_{max}),S_{max}\}$ 上进行评估。

  

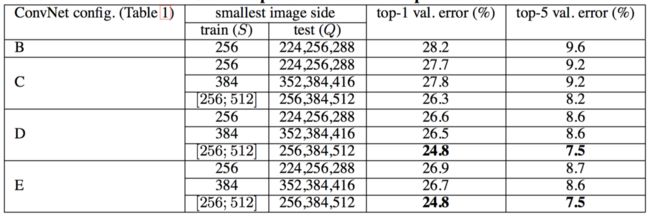
  测试时的尺度抖动导致了更好的性能（与在单一尺度上相同模型的评估相比，如前表所示）。

  如前所述，最深的配置（D和E）执行最佳，并且训练时的尺度抖动优于训练时使用固定最小边。

• 多剪裁图像评估

  下表中, 在所有的实验中训练尺度S从[256, 512]采样，三个测试尺度Q考虑：{256, 384, 512}。

  

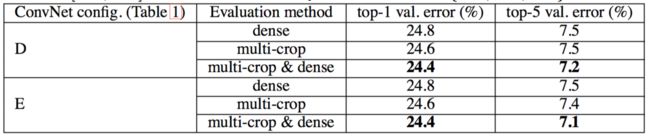
  在上表中，我们将稠密ConvNet评估与多裁剪图像评估进行比较。我们还通过平均其softmax输出来评估两种评估技术的互补性。可以看出，使用多裁剪图像表现比密集评估略好，而且这两种方法确实是互补的，因为它们的组合优于其中的每一种。如上所述，我们假设这是由于卷积边界条件的不同处理。

对比的结论

作者在对比各级网络时总结出了以下几个观点。

1. LRN层作用不大。
2. 越深的网络效果越好。
3. 1*1的卷积也是很有效的，但是没有3*3的卷积好，大一些的卷积核可以学习更大的空间特征。

结论

在这项工作中，我们评估了非常深的卷积网络（最多19个权重层）用于大规模图像分类。已经证明，表示深度有利于分类精度，并且深度大大增加的传统ConvNet架构（LeCun等，1989；Krizhevsky等，2012）可以实现ImageNet挑战数据集上的最佳性能。

VGG给我们的启示

https://www.jianshu.com/p/68ac04943f9e

VGGNet 探索的是神经网络的深度(depth)与其性能之间的关系

VGG通过反复堆叠3×3的小型卷积核和2×2的最大池化层，VGG成功构建了16-19层的卷积神经网络。是当时在论文发表前最深的深度网络。实际上，VGG在探索深度对神经网络影响的同时，其实本身广度也是很深的。那么：

神经网络的深度和广度对其本身的影响是什么呢？

• 卷积核的种类对应了网络的广度，卷积层数对应了网络的深度。这两者对网络的拟合都有影响。但是在现代深度学习中，大家普遍认为深度比广度的影响更加高。
• 宽度即卷积核的种类个数，在LeNet那篇文章里我们说了，权值共享(每个神经元对应一块局部区域，如果局部区域是10*10，那么就有100的权重参数，但如果我们把每个神经元的权重参数设置为一样，相当于每个神经元用的是同一个卷积核去卷积图像，最终两层间的连接只有 100 个参数 ！)可以大大减少我们的训练参数，但是由于使用了同一个卷积核，最终特征个数太少，效果也不会好，所以一般神经网络都会有多个卷积核，这里说明宽度的增加在一开始对网络的性能提升是有效的。但是，随着广度的增加，对网络整体的性能其实是开始趋于饱和，并且有下降趋势，因为过多的特征（一个卷积核对应发现一种特征）可能对带来噪声的影响。
• 深度即卷积层的个数，对网络的性能是极其重要的，ResNet已经表明越深的深度网络性能也就越好。深度网络自然集成了低、中、高层特征。多层特征可以通过网络的堆叠的数量（深度）来丰富其表达。挑战imagenet数据集的优秀网络都是采用较深的模型。网络的深度很重要，但是否能够简单的通过增加更多的网络层次学习更好的网络？这个问题的障碍就是臭名昭著的梯度消失(爆炸)问题，这从根本上阻碍了深度模型的收敛。
• 增加更多的卷积核可以发现更多的特征，但是特征是需要进行组合的，只有知道了特征之间的关系才能够更好的表达图片内容，而增加深度就是组合特征的过程。

VGG结构全部都采用较小的卷积核（3×3，部分1×1）

如何选择卷积核的大小？越大越好还是越小越好？

答案是小而深，单独较小的卷积核也是不好的，只有堆叠很多小的卷积核，模型的性能才会提升。

• 如上图所示，CNN的卷积核对应一个感受野，这使得每一个神经元不需要对全局图像做感受，每个神经元只感受局部的图像区域，然后在更高层，将这些感受不同局部的神经元综合起来就可以得到全局信息。这样做的一个好处就是可以减少大量训练的参数。
• VGG经常出现多个完全一样的3×3的卷积核堆叠在一起的情况，这些多个小型卷积核堆叠的设计其实是非常有效的。两个3×3的卷积层串联相当于1个5×5的卷积层，即一个像素会和周围5×5的像素产生关联，可以说感受野是5×5。同时，3个串联的3×3卷积层串联的效果相当于一个7×7的卷积层。除此之外，3个串联的3×3的卷积层拥有比一个7×7更少的参数量，只有后者的 (3×3×3) / (7×7) = 55%。最重要的是3个3×3的卷积层拥有比一个7×7的卷积层更多的非线性变换（前者可以使用三次ReLu激活，而后者只有一次）。

代码

架构

其中slim.conv2d默认的激活函数是relu.这个激活函数作用于输出的特征图.

net = slim.repeat(inputs, 2, slim.conv2d, 64, [3, 3], scope='conv1')
net = slim.max_pool2d(net, [2, 2], scope='pool1')
net = slim.repeat(net, 2, slim.conv2d, 128, [3, 3], scope='conv2')
net = slim.max_pool2d(net, [2, 2], scope='pool2')
net = slim.repeat(net, 3, slim.conv2d, 256, [3, 3], scope='conv3')
net = slim.max_pool2d(net, [2, 2], scope='pool3')
net = slim.repeat(net, 3, slim.conv2d, 512, [3, 3], scope='conv4')
net = slim.max_pool2d(net, [2, 2], scope='pool4')
net = slim.repeat(net, 3, slim.conv2d, 512, [3, 3], scope='conv5')
net = slim.max_pool2d(net, [2, 2], scope='pool5')

# Use conv2d instead of fully_connected layers.
net = slim.conv2d(net, 4096, [7, 7],
                  padding=fc_conv_padding, scope='fc6')
net = slim.dropout(net, dropout_keep_prob, is_training=is_training,
                   scope='dropout6')
net = slim.conv2d(net, 4096, [1, 1], scope='fc7')

# Convert end_points_collection into a end_point dict.
end_points = slim.utils.convert_collection_to_dict(end_points_collection)
if global_pool:
    net = tf.reduce_mean(net, [1, 2], keep_dims=True, name='global_pool')
    end_points['global_pool'] = net
if num_classes:
    net = slim.dropout(net, dropout_keep_prob, is_training=is_training,
                       scope='dropout7')
    net = slim.conv2d(net, num_classes, [1, 1],
                      activation_fn=None,
                      normalizer_fn=None,
                      scope='fc8')

预处理

❓

这里的关于随机翻转的预处理操作, slim 实现在训练里, 但是论文是说在测试里

训练

def preprocess_for_train(image,
                         output_height,
                         output_width,
                         resize_side_min=_RESIZE_SIDE_MIN,
                         resize_side_max=_RESIZE_SIDE_MAX):
  """Preprocesses the given image for training.

  Note that the actual resizing scale is sampled from
    [`resize_size_min`, `resize_size_max`].

  Args:
    image: A `Tensor` representing an image of arbitrary size.
    output_height: The height of the image after preprocessing.
    output_width: The width of the image after preprocessing.
    resize_side_min: The lower bound for the smallest side of the image for
      aspect-preserving resizing.
    resize_side_max: The upper bound for the smallest side of the image for
      aspect-preserving resizing.

  Returns:
    A preprocessed image.
  """
  resize_side = tf.random_uniform(
      [], minval=resize_side_min, maxval=resize_side_max+1, dtype=tf.int32)
  # 放缩
  image = _aspect_preserving_resize(image, resize_side)
  # 随机裁剪
  image = _random_crop([image], output_height, output_width)[0]
  # 重新调整形状
  image.set_shape([output_height, output_width, 3])
  image = tf.to_float(image)
  # 随机左右翻转
  image = tf.image.random_flip_left_right(image)
  # 减去均值
  return _mean_image_subtraction(image, [_R_MEAN, _G_MEAN, _B_MEAN])

测试

相比训练阶段,只是少了随机翻转.

def preprocess_for_eval(image, output_height, output_width, resize_side):
  """Preprocesses the given image for evaluation.

  Args:
    image: A `Tensor` representing an image of arbitrary size.
    output_height: The height of the image after preprocessing.
    output_width: The width of the image after preprocessing.
    resize_side: The smallest side of the image for aspect-preserving resizing.

  Returns:
    A preprocessed image.
  """
  image = _aspect_preserving_resize(image, resize_side)
  image = _central_crop([image], output_height, output_width)[0]
  image.set_shape([output_height, output_width, 3])
  image = tf.to_float(image)
  return _mean_image_subtraction(image, [_R_MEAN, _G_MEAN, _B_MEAN])