矢量场散度(divergence)和旋度(curl)及Helmholtz定理MATLAB计算
旋度
已给向量 F ⃗ = P i ⃗ + Q j ⃗ + R k ⃗ \vec F = P\,\vec i + Q\,\vec j + R\,\vec k F=Pi+Qj+Rk 则该向量的旋度表示为 r o t F ⃗ = ( R y − Q z ) i ⃗ + ( P z − R x ) j ⃗ + ( Q x − P y ) k ⃗ {\mathop{\rm rot}\nolimits}~~ \vec F = \left( {{R_y} - {Q_z}} \right)\vec i + \left( {{P_z} - {R_x}} \right)\vec j + \left( {{Q_x} - {P_y}} \right)\vec k rot F=(Ry−Qz)i+(Pz−Rx)j+(Qx−Py)k 定义Hamilton算子(表示空间各方向的全微分) ∇ \nabla ∇ 使得 ∇ = ∂ ∂ x i ⃗ + ∂ ∂ y j ⃗ + ∂ ∂ z k ⃗ \nabla = \frac{\partial }{{\partial x}}\,\,\vec i + \frac{\partial }{{\partial y}}\,\,\vec j + \frac{\partial }{{\partial z}}\,\,\vec k ∇=∂x∂i+∂y∂j+∂z∂k 使用它时就像在使用一个作用在函数上的函数。 ∇ f = ∂ f ∂ x i ⃗ + ∂ f ∂ y j ⃗ + ∂ f ∂ z k ⃗ \nabla f = \frac{{\partial f}}{{\partial x}}\,\,\vec i + \frac{{\partial f}}{{\partial y}}\,\,\vec j + \frac{{\partial f}}{{\partial z}}\,\,\vec k ∇f=∂x∂fi+∂y∂fj+∂z∂fk 利用▽,可将旋度定义式转化为叉积形式: c u r l F ⃗ = ∇ × F ⃗ = ( i ⃗ j ⃗ k ⃗ ∂ ∂ x ∂ ∂ y ∂ ∂ z P Q R ) {\mathop{\rm curl~~}\nolimits} \vec F = \nabla \times \vec F = \left( {\begin{array}{c}{\vec i}&{\vec j}&{\vec k}\\{\displaystyle \frac{\partial }{{\partial x}}}&{\displaystyle \frac{\partial }{{\partial y}}}&{\displaystyle \frac{\partial }{{\partial z}}}\\P&Q&R\end{array}} \right) curl F=∇×F=⎝⎜⎜⎛i∂x∂Pj∂y∂Qk∂z∂R⎠⎟⎟⎞ 矢量场的旋度有以下性质:如果 f ( x , y , z ) f\left( {x,y,z} \right) f(x,y,z)有连续二阶偏导数,则 r o t ( ∇ f ) = 0 ⃗ {\mathop{\rm rot}\nolimits} \left( {\nabla f} \right) = \vec 0 rot(∇f)=0此性质由连续二阶偏导数与求导顺序无关的性质(fzy=fyz等等)即可得出。
2.如果F是保守场(某标量势的梯度),则 r o t F ⃗ = 0 ⃗ {\mathop{\rm rot~}\nolimits} \vec F = \vec 0 rot F=0由保守场性质和1立即得此结论。
3. 如 果 F ⃗ 定 义 在 R 3 上 具 有 连 续 一 阶 偏 导 数 , 并 且 r o t F ⃗ = 0 ⃗ , 则 F ⃗ 是 一 个 保 守 场 。 3.~~~如果\vec{F}定义在{\mathbb{R}^3}上具有连续一阶偏导数,并且{\mathop{\rm rot}\nolimits} \vec F = \vec 0 ,则 \vec{F}是一个保守场。 3. 如果F定义在R3上具有连续一阶偏导数,并且rotF=0,则F是一个保守场。 例 如 , 要 确 定 F ⃗ = x 2 y i ⃗ + x y z j ⃗ − x 2 y 2 k ⃗ 是 否 为 保 守 场 , 只 需 要 计 算 F ⃗ 的 旋 度 判 断 是 否 为 0 即 可 。 例如,要确定\vec F = {x^2}y\,\vec i + xyz\,\vec j - {x^2}{y^2}\,\vec k 是否为保守场,只需要计算\vec F的旋度判断是否为0即可。 例如,要确定F=x2yi+xyzj−x2y2k是否为保守场,只需要计算F的旋度判断是否为0即可。 c u r l F ⃗ = ∣ i ⃗ j ⃗ k ⃗ ∂ ∂ x ∂ ∂ y ∂ ∂ z x 2 y x y z − x 2 y 2 ∣ = − 2 x 2 y i ⃗ + y z k ⃗ − ( − 2 x y 2 j ⃗ ) − x y i ⃗ − x 2 k ⃗ = − ( 2 x 2 y + x y ) i ⃗ + 2 x y 2 j ⃗ + ( y z − x 2 ) k ⃗ ≠ 0 ⃗ 于 是 得 出 不 是 保 守 的 。 {\mathop{\rm curl}\nolimits} \vec F = \left| {\begin{array}{c}{\vec i}&{\vec j}&{\vec k}\\{\displaystyle \frac{\partial }{{\partial x}}}&{\displaystyle \frac{\partial }{{\partial y}}}&{\displaystyle \frac{\partial }{{\partial z}}}\\{{x^2}y}&{xyz}&{ - {x^2}{y^2}}\end{array}} \right|\\ = - 2{x^2}y\,\vec i + yz\,\vec k - \left( { - 2x{y^2}\,\vec j} \right) - xy\,\vec i - {x^2}\vec k\\ = - \left( {2{x^2}y + xy} \right)\vec i + 2x{y^2}\,\vec j + \left( {yz - {x^2}} \right)\vec k \ne \vec 0 \\于是得出不是保守的。 curlF=∣∣∣∣∣∣∣∣i∂x∂x2yj∂y∂xyzk∂z∂−x2y2∣∣∣∣∣∣∣∣=−2x2yi+yzk−(−2xy2j)−xyi−x2k=−(2x2y+xy)i+2xy2j+(yz−x2)k=0于是得出不是保守的。旋度的推导
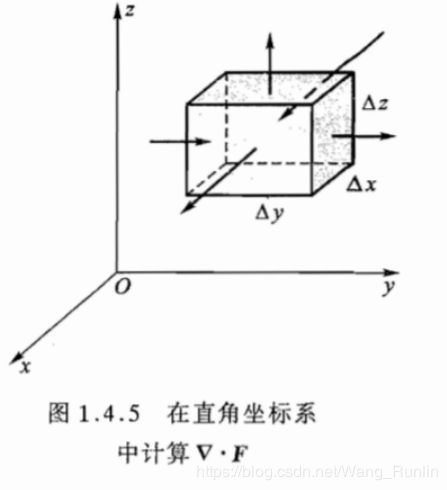
利用F二阶的可微性质,通过选取平行面积微元,每步只计算三维空间的一个维度的旋度来实现的,从《电磁场与电磁波》 (谢处方等著,高等教育出版社)摘录如下:(关键在理解利用二阶可微性质将两条非临边对旋度的贡献用二阶微分表示和约去的过程,还有叉乘展开的过程。书上思路比较清晰,不需赘述。)


matlab 中已有计算旋度的函数curl。具体参见matlab官方文档_curl。对于其中用到的meshgird函数,参见matlab官方文档_meshgrid
根据旋度的计算式,很快推得斯托克斯公式:
∫ S ∇ × F ⋅ d S = ∮ C F ⋅ d l \int_{S} \nabla\times\textbf F \cdot d\textbf S=\oint_{C} \textbf F \cdot d\textbf l ∫S∇×F⋅dS=∮CF⋅dl将曲面S划分成很多小面元、对每一个面元沿边缘取最大环流(也即这点旋度)并相加,发现除曲面的边沿,其他部分都互相抵消。对于每一个小回路,都有 ∮ C n F ⋅ d l = r o t n F d S n = ∇ × F ⋅ d S n \oint_{C_{n}}\textbf F \cdot d\textbf l=rot_{n}\textbf FdS_{n}=\nabla\times\textbf F\cdot d\textbf S_{n} ∮CnF⋅dl=rotnFdSn=∇×F⋅dSn求和便得斯托克斯公式
散度
散度表示矢量场在一个点附近的通量特性。散度的定义式是 d i v F = lim Δ V → 0 ∮ S F ⋅ d S Δ V div ~\textbf F=\lim_{\Delta\textbf V \to 0}\frac{\oint_{S}\textbf F \cdot d\textbf S} {\Delta V} div F=ΔV→0limΔV∮SF⋅dS散度的推导与旋度相似,都是分别从某一个维度分析,只是取的是体积元,计算的是面积分,过程清晰,直接摘录。(以下推导过程仍来自《电磁场与电磁波》,谢处方等著)




类似由旋度得出斯托克斯定理,由散度的推导过程,很快得到散度定理(高斯定理): ∫ V ∇ ⋅ F d V = ∮ S F ⋅ d S \int_{V}\nabla\cdot\textbf{F}d\textbf{V}=\oint_{S}\textbf{F}\cdot d\textbf{S} ∫V∇⋅FdV=∮SF⋅dSmatlab中,散度也有预先定义的函数,参见matlab文档_divergence
Helmholtz定理
在有限的区域V内,任一矢量场由它的散度、旋度和边界条件唯一确定(矢量场F可以用一个标量函数的梯度和一个矢量函数的旋度之和来表示),表示为
![]()
其中,

证明参见Helmholtz_Decomposition
这里,使用matlab嵌入chebfun模块展示它的过程:
f = spherefunv( @(x,y,z) y.*z.*cos(x.*y.*z), ...
@(x,y,z) x.*z.*sin(4*x+.1*y+5*z.^2), @(x,y,z) 1+x.*y.*z );
quiver3( f ), view([-36 8])
这个矢量场是 F = y z c o s ( x y z ) e ⃗ x + x z s i n ( 4 x + y + 5 z 2 ) e y ⃗ + ( x y z + 1 ) e ⃗ z \textbf F=yzcos(xyz){\vec \textbf e_{x}}+xzsin(4x+y+5z^2)\vec {\textbf e_{y}}+(xyz+1)\vec \textbf {e}_{z} F=yzcos(xyz)ex+xzsin(4x+y+5z2)ey+(xyz+1)ez利用tangent命令,在球面上作出场的形状,如图。
f = tangent( f );
quiver3( f ), view([-36 8])

计算无旋分量。由于旋度的梯度是0,所以 ∇ ⋅ f = ∇ ⋅ ∇ ϕ = ∇ 2 ϕ , \nabla \cdot \mathbf{f} = \nabla \cdot \nabla \phi = \nabla^2 \phi, ∇⋅f=∇⋅∇ϕ=∇2ϕ,根据球面上的泊松方程 ∇ 2 u = f , ∫ S 2 u ( x , y , z ) d x d y d z = 0 \nabla^2u=f,~~~~\int_{\textbf S^2}u(x,y,z)dxdydz=0 ∇2u=f, ∫S2u(x,y,z)dxdydz=0
可视化过程如下. 蓝色环相当于等势线. 发现在球的两极, 无旋分量较小. 比对上下两图, 发现上图花瓣状的扭线在下图中几乎看不出来.
phi = spherefun.poisson( divergence(f), 0, 251 );
quiver3( gradient( phi ) ), hold on,
LW = 'linewidth';
contour( phi, 'b-', LW , 2 ),
title('Curl-free component of f')
view([-36 8]), hold off
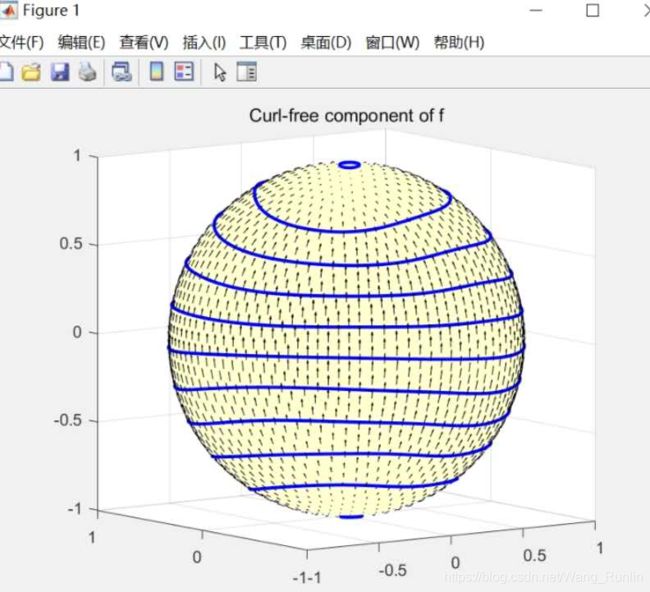
为证实这是无旋分量,使用norm( vorticity( gradient( phi ) ) ),(所得无旋分量旋度矩阵的范数)求得结果约为0.
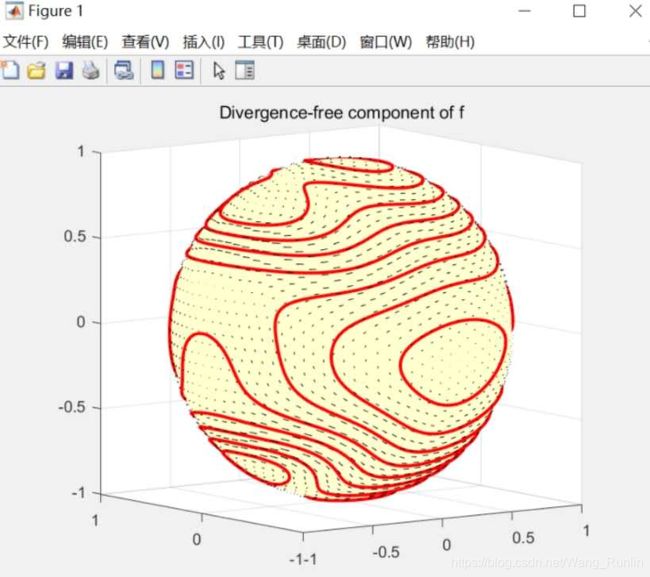
计算无散分量. 如下. 由于球面梯度场的涡度为零,有 n ^ ⋅ ( ∇ × f ) = n ^ ⋅ ( ∇ × ψ ) . \hat{\mathbf{n}} \cdot (\nabla \times \mathbf{f}) = \hat{\mathbf{n}} \cdot (\nabla \times \psi). n^⋅(∇×f)=n^⋅(∇×ψ). 由于球面标量势的表面旋度的涡度(实际也是旋度)相当于对该势应用拉普拉斯算子(因为标量势梯度的散度是0), 又得出 n ^ ⋅ ( ∇ × f ) = ∇ 2 ψ . \hat{\mathbf{n}} \cdot (\nabla \times \mathbf{f}) = \nabla^2 \psi. n^⋅(∇×f)=∇2ψ.这样便可用如下方式求并可视化无散分量:
psi = spherefun.poisson( vorticity(f), 0, 251 );
quiver3( curl( psi ) ), hold on,
contour( psi, 'r-', LW , 2 ),
title('Divergence-free component of f')
view([-36 8]), hold off
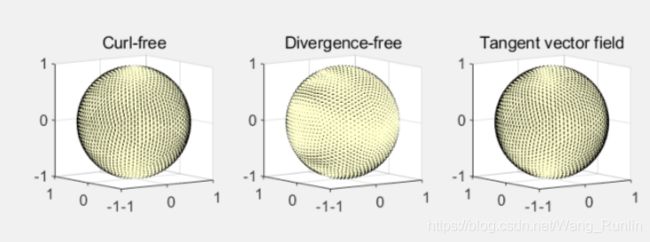
subplot(1,3,1)
quiver3( gradient( phi ) ), title('Curl-free'), view([-36 8])
subplot(1,3,2)
quiver3( curl( psi ) ), title('Divergence-free'), view([-36 8])
subplot(1,3,3)
quiver3( f ), title('Tangent vector field'), view([-36 8])
[phi, psi] = helmholtzdecomp( f );
clf, quiver( f ), hold on
contour( phi, 'b-', LW , 2 )
contour( psi, 'r-', LW , 2 )
title('f (arrows), \phi (blue), and \psi (red)')
view([-36 8])