『论文笔记』Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks!
| Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks! |
文章目录
- 一. Faster R-CNN的思想
- 1.1. R-CNN,Fast R-CNN,Faster R-CNN对比
- 1.2. Faster R-CNN的网络结构
- 二. 区域生成网络(RPN)详解
- 2.1. 特征提取
- 2.2. 候选区域(anchor)
- 2.3. 边框回归
- 2.4. 候选框修正
- 三. RoI Pooling层
- 3.1. 为何需要RoI Pooling
- 3.2. RoI Pooling原理
- 四. 分类和框回归
- 五. Faster R-CNN训练
- 参考博客
- 本文是继(2013)R-CNN、(2014ECCV)SSPNet、(2015ICCV)Fast R-CNN之后,目标检测界的领军人物Ross Girshick团队(链接)在2015年的又一力作。
- Faster R-CNN下载链接
一. Faster R-CNN的思想
1.1. R-CNN,Fast R-CNN,Faster R-CNN对比
从R-CNN到Fast RCNN,再到本文的Faster R-CNN,目标检测的四个基本步骤 (1.候选区域生成,2.特征提取,3.分类,4.位置精修)终于被统一到一个深度网络框架之内。所有计算没有重复,完全在GPU中完成,大大提高了运行速度。
- 三者关系如下图:

- 三者对比如下表:

- faster RCNN可以简单地看做 “区域生成网络(RPN)+fast RCNN“ 的系统,用区域生成网络代替fast RCNN中的Selective Search方法。本篇论文着重解决了这个系统中的三个问题:
- 如何设计区域生成网络
- 如何训练区域生成网络
- 如何让区域生成网络和fast RCNN网络共享特征提取网络
1.2. Faster R-CNN的网络结构
Faster R-CNN统一的网络结构如下图所示,可以简单看作RPN网络+Fast R-CNN网络。
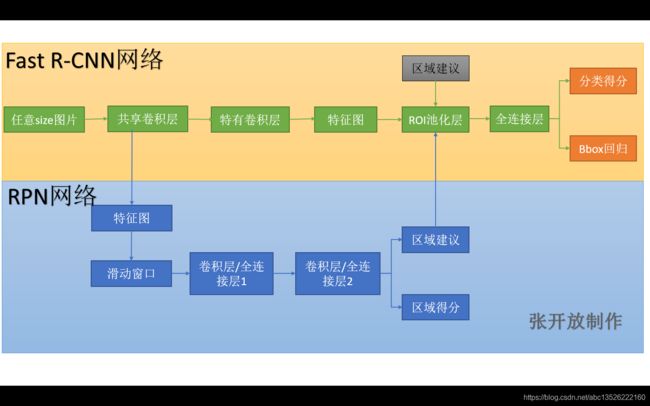
注意:上图Fast R-CNN中含特有卷积层,我认为不是所有卷积层都参与共享。具体步骤如下:
- 1、首先向CNN网络【ZF或VGG-16】输入任意大小图片 M × N M×N M×N;
- 2、经过CNN网络前向传播至最后共享的卷积层,一方面得到供RPN网络输入的特征图,另一方面继续前向传播至特有卷积层,产生更高维特征图;
- 3、供RPN网络输入的特征图经过RPN网络得到区域建议和区域得分,并对区域得分采用非极大值抑制【阈值为0.7】,输出其Top-N【文中为300】得分的区域建议给RoI池化层;
- 4、第2步得到的高维特征图和第3步输出的区域建议同时输入RoI池化层,提取对应区域建议的特征;
- 5、第4步得到的区域建议特征通过全连接层后,输出该区域的分类得分以及回归后的bounding-box。
二. 区域生成网络(RPN)详解
- 基本设想是:在提取好的特征图上,对所有可能的候选框进行判别。由于后续还有位置精修步骤,所以候选框实际比较稀疏。
2.1. 特征提取
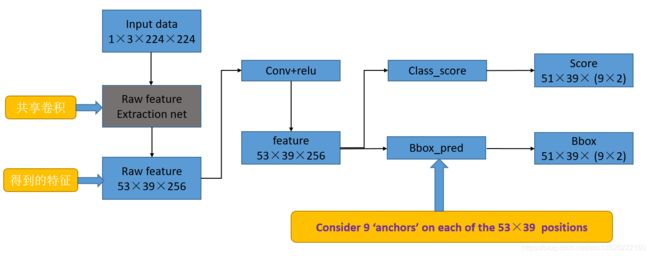
- RPN还是需要使用一个CNN网络对原始图片提取特征。为了方便读者理解,不妨设这个前置的CNN提取的特征为 51 × 39 × 256 51×39×256 51×39×256,即高为51,宽为39,通道数为256.对这个卷积特征再进行一次卷积计算,保持宽、高、通道数不变,再次得到一个 51 × 39 × 256 51×39×256 51×39×256的特征。
- 为了方便叙述,先来定义一个 “位置” 的概念:对于一个 51 × 39 × 256 51×39×256 51×39×256的卷积特征,称它一共有 51 × 39 51×39 51×39个"位置"。让新的卷积特征的每一个"位置"都"负责”原图中对应位置的9种尺寸框的检测,检测的目标是判断框中是否存在一个物体,因此共用 51 × 39 × 9 51×39×9 51×39×9个“框”。 在Faster R-CNN原论文中,将这些框都统一称为 “anchor”。
2.2. 候选区域(anchor)
- 特征可以看做一个尺度 51 × 39 51×39 51×39 的256通道图像,对于该图像的每一个位置,考虑9个可能的候选窗口:三种面积分别是 128 × 128 , 256 × 256 , 512 × 512 128×128,256×256,512×512 128×128,256×256,512×512,每种面积又分成3种长宽比,分别是 2 : 1 , 1 : 2 , 1 : 1 2:1,1:2,1:1 2:1,1:2,1:1,所以每个位置有 3 × 3 = 9 3×3=9 3×3=9个anchor 。这些候选窗口称为anchors,接着就是通过这些anchors引入了检测中常用到的多尺度方法(检测各种大小的目标),下图示出 51 × 39 51×39 51×39个anchor中心,以及9种anchor示例。 注意:这里每3个同比例的画在了不同位置(为了容易发现),实际每个位置都有9个,第2个图所示。

|
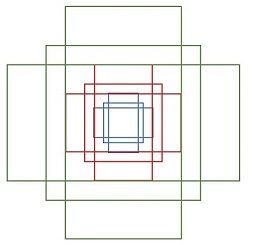
|
|---|
对于这 51 × 39 51×39 51×39个位置和 51 × 39 × 9 51×39×9 51×39×9个anchor,下图展示了接下来每个位置的计算步骤:
- 设 k k k为单个位置对应的 a n c h o r anchor anchor 的个数,此时 k = 9 k=9 k=9,通过增加一个 3 × 3 3×3 3×3滑动窗口操作以及两个卷积层完成区域建议功能;
- 使用一个小网络在最后卷积得到的特征图上进行滑动扫描,这个滑动网络每次与特征图上 n × n n×n n×n(论文中 n = 3 n=3 n=3)的窗口全连接(图像的有效感受野很大,ZF是171像素,VGG是228像素),然后映射到一个低维向量(256d for ZF / 512d for VGG),最后将这个低维向量送入到两个全连接层,即bbox回归层(reg)和box分类层(cls)。sliding window的处理方式保证reg-layer和cls-layer关联了conv5-3的全部特征空间。
- 对应每个滑窗位置输出 k k k 个区域得分,表示该位置的 a n c h o r anchor anchor 为物体的概率,这部分总输出长度为 2 × k 2×k 2×k(一个anchor对应两个输出:是物体的概率+不是物体的概率)和 k k k 个回归后的区域建议(框回归),一个 a n c h o r anchor anchor对应4个框回归参数,因此框回归部分的总输出的长度为 4 × k 4×k 4×k,并对得分区域进行非极大值抑制后输出得分Top-N(文中为300)区域,告诉检测网络应该注意哪些区域,本质上实现了Selective Search、EdgeBoxes等方法的功能。

- reg layer:预测proposal的anchor对应的proposal的 ( x , y , w , h ) (x,y,w,h) (x,y,w,h);
- cls layer:判断该proposal是前景(object)还是背景(non-object);
2.3. 边框回归
如下图所示绿色框为飞机的Ground Truth(GT),红色为提取的foreground anchors,即便红色的框被分类器识别为飞机,但是由于红色的框定位不准,这张图相当于没有正确的检测出飞机。所以我们希望采用一种方法对红色的框进行微调,使得foreground anchors和GT更加接近。

对于窗口一般使用四维向量 ( x , y , w , h ) (x, y, w, h) (x,y,w,h) 表示,分别表示窗口的中心点坐标和宽高。
我们使用 A A A 表示原始的foreground anchor,使用 G G G 表示目标的ground truth,我们的目标是寻找一种关系,使得输入原始的Anchor A经过映射到一个和真实框 G G G更接近的回归窗口 G ′ G^{\prime} G′,即:
- 给定: a n c h o r anchor anchor A = ( A x , A y , A w , A h ) A=(A_{x}, A_{y}, A_{w}, A_{h}) A=(Ax,Ay,Aw,Ah) 和 G T = [ G x , G y , G w , G h ] GT=[G_{x}, G_{y}, G_{w}, G_{h}] GT=[Gx,Gy,Gw,Gh]
- 寻找一种变换 F F F,使得: F ( A x , A y , A w , A h ) = ( G x ′ , G y ′ , G w ′ , G h ′ ) , F(A_{x}, A_{y}, A_{w}, A_{h})=(G_{x}^{'}, G_{y}^{'}, G_{w}^{'}, G_{h}^{'}), F(Ax,Ay,Aw,Ah)=(Gx′,Gy′,Gw′,Gh′),其中 ( G x ′ , G y ′ , G w ′ , G h ′ ) ≈ ( G x , G y , G w , G h ) (G_{x}^{'}, G_{y}^{'}, G_{w}^{'}, G_{h}^{'})≈(G_{x}, G_{y}, G_{w}, G_{h}) (Gx′,Gy′,Gw′,Gh′)≈(Gx,Gy,Gw,Gh)

那么经过何种变换 F F F才能从图10中的 a n c h o r anchor anchor A A A变为 G ′ G' G′ 呢? 比较简单的思路就是:
-
先做平移
G x ′ = A x + A w ⋅ d x ( A ) G y ′ = A y + A h ⋅ d y ( A ) \begin{aligned} G_{x}^{\prime} &=A_{x}+A_{w} \cdot d_{x}(A) \\\\ G_{y}^{\prime} &=A_{y}+A_{h} \cdot d_{y}(A) \end{aligned} Gx′Gy′=Ax+Aw⋅dx(A)=Ay+Ah⋅dy(A) -
再做缩放
G w ′ = A w ⋅ exp ( d w ( A ) ) G h ′ = A h ⋅ exp ( d h ( A ) ) \begin{array}{l}{G_{w}^{\prime}=A_{w} \cdot \exp \left(d_{w}(A)\right)} \\\\ {G_{h}^{\prime}=A_{h} \cdot \exp \left(d_{h}(A)\right)}\end{array} Gw′=Aw⋅exp(dw(A))Gh′=Ah⋅exp(dh(A)) -
上面4个公式中,我们需要学习4个参数,分别是 d x ( A ) , d y ( A ) , d w ( A ) , d h ( A ) d_{x}(A),d_{y}(A),d_{w}(A),d_{h}(A) dx(A),dy(A),dw(A),dh(A) ,当输入的anchor A与GT相差较小时,可以认为这种变换是一种线性变换, 那么就可以用线性回归来建模对窗口进行微调 (注意,只有当anchors A和GT比较接近时,才能使用线性回归模型,否则就是复杂的非线性问题了)。
-
接下来的问题就是如何通过线性回归获得 d x ( A ) , d y ( A ) , d w ( A ) , d h ( A ) d_{x}(A),d_{y}(A),d_{w}(A),d_{h}(A) dx(A),dy(A),dw(A),dh(A) 了。线性回归就是给定输入的特征向量 X X X, 学习一组参数 W W W, 使得经过线性回归后的值跟真实值 Y Y Y 非常接近,即 Y = W X Y=WX Y=WX。对于该问题,输入 X X X 是cnn feature map,定义为 Φ Φ Φ;同时还有训练传入A与GT之间的变换量,即 ( t x , t y , t w , t h ) (t_{x}, t_{y}, t_{w}, t_{h}) (tx,ty,tw,th) 。输出是 d x ( A ) , d y ( A ) , d w ( A ) , d h ( A ) d_{x}(A),d_{y}(A),d_{w}(A),d_{h}(A) dx(A),dy(A),dw(A),dh(A) 四个变换。那么目标函数可以表示为:
d ∗ ( A ) = w ∗ T ⋅ ϕ ( A ) d_{*}(A)=w_{*}^{T} \cdot \phi(A) d∗(A)=w∗T⋅ϕ(A)
其中 ϕ ( A ) \phi(A) ϕ(A)是对应anchor的feature map组成的特征向量, W ∗ W_* W∗ 是需要学习的参数, d ∗ ( A ) d_*(A) d∗(A) 是得到的预测值( ∗ * ∗ 表示 x , y , w , h , x,y,w,h, x,y,w,h,也就是每一个变换对应一个上述目标函数)。为了让预测值 d ∗ ( A ) d_*(A) d∗(A) 与真实值 t ∗ t_* t∗ 差距最小,设计损失函数:
loss = ∑ i = 1 N ( t ∗ i − w ^ ∗ T ⋅ ϕ ( A i ) ) 2 \operatorname{loss} =\sum_{i=1}^{N}\left(t_{*}^{i}-\hat{w}_{*}^{T} \cdot \phi\left(A^{i}\right)\right)^{2} loss=i=1∑N(t∗i−w^∗T⋅ϕ(Ai))2 -
函数优化目标为:
W ^ ∗ = argmin W ∗ ∑ i n ( t ∗ i − W ∗ T ⋅ ϕ ( A i ) ) 2 + λ ∥ W ∗ ∥ 2 \hat{W}_{*}=\operatorname{argmin}_{W_{*}} \sum_{i}^{n}\left(t_{*}^{i}-W_{*}^{T} \cdot \phi\left(A^{i}\right)\right)^{2}+\lambda\left\|W_{*}\right\|^{2} W^∗=argminW∗i∑n(t∗i−W∗T⋅ϕ(Ai))2+λ∥W∗∥2 -
需要说明,只有在GT与需要回归框位置比较接近时,才可近似认为上述线性变换成立。说完原理,对应于Faster RCNN原文,foreground anchor与ground truth之间的平移量 ( t x , t y ) (t_x, t_y) (tx,ty)与尺度因子 ( t w , t h ) (t_w, t_h) (tw,th) 如下:
t x = ( x − x a ) / w a t y = ( x − y a ) / h a t w = log ( w / w a ) t h = log ( h / h a ) \begin{array}{c}{t_{x}=\left(x-x_{a}\right) / w_{a} \quad t_{y}=\left(x-y_{a}\right) / h_{a}} \\\\ {t_{w}=\log \left(w / w_{a}\right) \quad t_{h}=\log \left(h / h_{a}\right)}\end{array} tx=(x−xa)/waty=(x−ya)/hatw=log(w/wa)th=log(h/ha)
对于训练bouding box regression网络回归分支,输入是cnn feature Φ Φ Φ,监督信号是Anchor与GT的差距 ( t x , t y , t w , t h ) (t_x, t_y, t_w, t_h) (tx,ty,tw,th),即训练目标是:输入 Φ Φ Φ 的情况下使网络输出与监督信号尽可能接近。那么当bouding box regression工作时,再输入 Φ Φ Φ 时,回归网络分支的输出就是每个Anchor的平移量和变换尺度 ( t x , t y , t w , t h ) (t_x, t_y, t_w, t_h) (tx,ty,tw,th),显然即可用来修正Anchor位置了。
2.4. 候选框修正
在得到每一个候选区域 a n c h o r anchor anchor A A A 的修正参数 ( d x ( A ) , d y ( A ) , d w ( A ) , d h ( A ) ) (dx(A),dy(A),dw(A),dh(A)) (dx(A),dy(A),dw(A),dh(A))之后,我们就可以计算出精确的 a n c h o r anchor anchor,然后按照物体的区域得分从大到小对得到的 a n c h o r anchor anchor 排序,然后提出一些宽或者高很小的 a n c h o r anchor anchor (获取其它过滤条件),再经过非极大值抑制抑制,取前Top-N的 a n c h o r s anchors anchors,然后作为 p r o p o s a l s proposals proposals (候选框)输出,送入到RoI Pooling层。
三. RoI Pooling层
RoI Pooling层负责收集所有的候选框,并计算每一个候选框的特征图,然后送入后续网络,从Faster RCNN的结构图我们可以看到RoI Pooling层有两个输入:
- 原始的特征图;
- RPN网络输出的候选框;
3.1. 为何需要RoI Pooling
先来看一个问题:对于传统的CNN(如AlexNet,VGG),当网络训练好后输入的图像尺寸必须是固定值(全连接层的限制,具体的解释可以参考我这篇文章:论文阅读笔记:(SSPNet)),同时网络输出也是固定大小的vector or matrix。如果输入图像大小不定,这个问题就变得比较麻烦。有2种解决办法:
- 从图像中crop(切割)一部分传入网络,但是crop后破坏了图像的完整结构
- 将图像warp(缩放)成需要的大小后传入网络,但是warp破坏了图像原始形状信息

3.2. RoI Pooling原理
我们把每一个候选框的特征图水平和垂直分为pooled_w(文章中为7)和pooled_h(7)份,对每一份进行最大池化处理,这样处理后,即使大小不一样的候选区,输出大小都一样,实现了固定长度的输出:

- 然后我们把Top-N个固定输出( 7 × 7 = 49 7×7=49 7×7=49)连接起来,组成特征向量,大小为 T o p − N × 49 Top−N×49 Top−N×49,这里可以把Top-N看做样本数,49看做每一个样本的特征维数,送入全连接层。
四. 分类和框回归
通过RoI Pooling层我们已经得到所有候选区组成的特征向量,然后送入全连接层和softmax计算每个候选框具体属于哪个类别,输出类别的得分;同时再次利用框回归获得每个候选区相对实际位置的偏移量预测值,用于对候选框进行修正,得到更精确的目标检测框。

- 这里我们来看看全连接层,由于全连接层的参数w和b大小都是固定大小的,假设大小为 49 × 26 49×26 49×26,那么输入向量的维度就要为 T o p − N × 49 Top−N×49 Top−N×49,所以这就说明了RoI Pooling的重要性。
五. Faster R-CNN训练
Faster R-CNN的训练,是在已经预训练好的model(如VGG_CNN_M_1024,VGG,ZF)的基础上继续进行训练。实际中训练过程分为6个步骤:详细参考知乎大神的博客!
参考博客
本文参考了许多优秀作者的文章,虽然有些具体细节还没有搞懂,下一步阅读代码,在这里表示衷心的感谢!
- 【目标检测】Faster RCNN算法详解
- Faster R-CNN - 目标检测详解
- https://blog.csdn.net/lk123400/article/details/54343550
- https://www.cnblogs.com/zyly/p/9247863.html
- 一文读懂Faster RCNN(这位大佬讲的很细、相信这看了这篇文章,对Faster RCNN的实现细节你会有了更深的了解)
- https://www.cnblogs.com/zyly/p/9247863.html