学习LeNet(网络讲解+代码)
LeNet
(新手入门,如理解有误感谢指正)
LeNet原论文地址
原论文共有了11个部分,我们所听说的LeNet-5是在Section II第二部分讲解的,第一部分是一些背景介绍,后面部分则是一些实验,可以自行阅读论文。
不算输入层,LeNet-5一共有7层网络用来预测手写数字0-9,如图1(来自论文)所示:
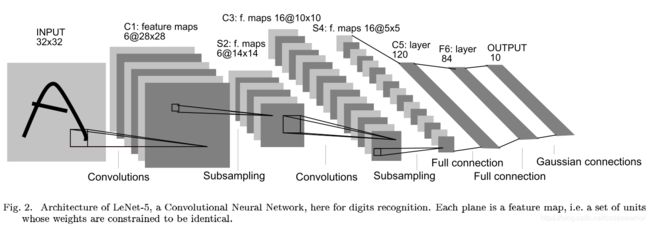
可以看到它是由Convolutional layer ( C1) + Subsampling layer ( S2) + Convolutional layer ( C3) + Subsampling layer ( S4) + Convolutional layer ( C5) + Fully connected layer ( F6) + Fully connected layer ( Output)
卷积层特征图输出尺寸计算公式:
M = N − F + 2 P S + 1 M = \frac{N-F+2P}{S}+1 M=SN−F+2P+1
其中N是输入的尺寸,即 N × N N\times N N×N的输入,F是卷积核(filter)的尺寸,即 F × F F\times F F×F的卷积核,P是padding,S是stride步长
Input:
32 × 32 32\times 32 32×32 的图像
C1:
6个卷积核
卷积核尺寸 5 × 5 5\times 5 5×5(注意通常说卷积核尺寸的时候忽略了深度,通常卷积核深度和输入图的深度相同,这里相当于是 1 × 5 × 5 1\times 5 \times 5 1×5×5)
步长stride为1
无填充padding
该层总共需要训练的参数个数为 6 × ( 1 × 5 × 5 + 1 ) = 156 6\times (1\times 5 \times 5 + 1) = 156 6×(1×5×5+1)=156(注意括号里为什么+1,因为每个卷积核还要有一个偏置项,6个卷积就又多6个参数)
输出每个特征图(feature map)的尺寸为 32 − 5 + 0 1 + 1 = 32 − 4 = 28 \frac{32-5+0}{1}+1 = 32-4=28 132−5+0+1=32−4=28,所以每个特征图是 28 × 28 28\times 28 28×28的,6个卷积核得到了深度为6的特征图,即 6 × 28 × 28 6\times 28\times 28 6×28×28
S2:
下采样层,实际上使用的是average pooling
采样核尺寸 2 × 2 2\times 2 2×2
步长stride为2
无填充padding
输出的每个特征图尺寸为 28 − 2 + 0 2 + 1 = 14 \frac{28-2+0}{2}+1 = 14 228−2+0+1=14,深度不变,所以输出特征图尺寸为 6 × 14 × 14 6\times 14 \times 14 6×14×14
图3
每次把采样的四个点像素求平均,然后乘一个需要训练的参数,再加个偏执,最后通过sigmoid非线性激活函数
这样的话,每一层深度上的采样需要2个参数,输入的深度是6,就是12个参数需要训练
C3:
16个卷积核
卷积核尺寸 5 × 5 5\times 5 5×5(这里比较有意思,按常理来说,由于上一层的输入图的深度是6,那么每个卷积核的实际尺寸应该是 6 × 5 × 5 6\times5\times5 6×5×5,但是论文没有简单的这么做下面会说)
步长stride为1
无填充padding
输出特征图的尺寸 14 − 5 + 0 1 + 1 = 10 \frac{14-5+0}{1}+1 = 10 114−5+0+1=10,16个卷积核得到深度为16的特征图,因此最终的输出特征图尺寸为 16 × 10 × 10 16\times10\times10 16×10×10
图5
一般来说第一个卷积核和 6 × 14 × 14 6\times14\times14 6×14×14的输入作用形成 16 × 10 × 10 16\times10\times10 16×10×10输出的第一层,第二个卷积核和 6 × 14 × 14 6\times14\times14 6×14×14的输入作用形成 16 × 10 × 10 16\times10\times10 16×10×10输出的第二层,以此类推得到第三层,…第十六层。
那么每个卷积核和前面 6 × 14 × 14 6\times14\times14 6×14×14的输入作用,卷积核的深度往往等于输入的深度,但是论文中在该层的做法不同,它没有使用输入的全部深度,而是一个子集,也就是说C3的卷积核深度并不简单的都是6。
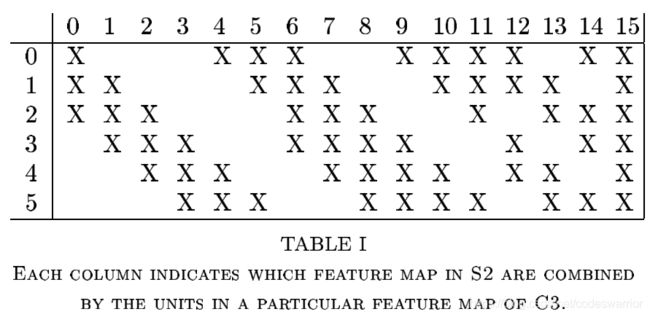
我们看一下论文中的这个表,注意他是从0开始标号,竖着看6个,代表输入特征图的6个层或者说6个channel,横着看16个,就代表输出特征图的16层了,因为输出深度16嘛。
这个表的意思是,输出特征图的第一层是第一个卷积核和输入特征图的前三层作用得到的,也就是说第一个卷积核的尺寸实际上是 3 × 5 × 5 3\times5\times5 3×5×5
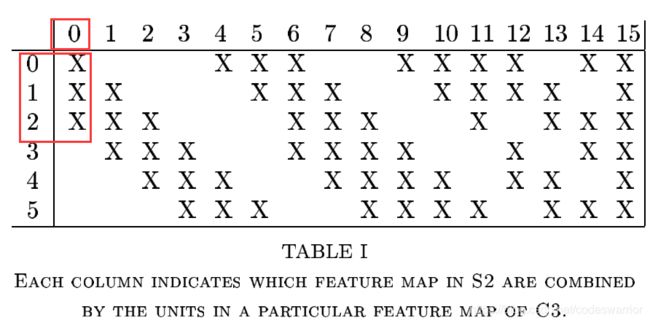
那么其实我们看表可以发现输出特征图的前6层(0-5)都是卷积核和输入特征图的连续的3层作用得到的,那么前六个卷积核的实际尺寸就是 3 × 5 × 5 3\times5\times5 3×5×5
同理,输出特征图后面的6层(6-11)是卷积核和输入特征图 连续的4层作用得到的,那么这6个卷积核的实际尺寸就是 4 × 5 × 5 4\times5\times5 4×5×5
再往后3层(12-14)是卷积核和输入特征图 不连续的4层作用得到的,这3个卷积核的实际尺寸也是 4 × 5 × 5 4\times5\times5 4×5×5
最后一层,才是使用了输入特征图的全部层,最后这个卷积核的实际尺寸才是 6 × 5 × 5 6\times5\times5 6×5×5
根据上面这么一通分析,我们就可以计算一下C3需要训练多少参数了
( 3 × 5 × 5 + 1 ) × 6 + ( 4 × 5 × 5 + 1 ) × ( 6 + 3 ) + ( 6 × 5 × 5 + 1 ) = 1516 (3\times5\times5+1)\times6+(4\times5\times5+1)\times(6+3)+(6\times5\times5+1)=1516 (3×5×5+1)×6+(4×5×5+1)×(6+3)+(6×5×5+1)=1516
括号里加1是每个卷积核的偏置项
S4:
恭喜你坚持到了这里,估计刚才的C3那一层的分析应该是LeNet-5中最难理解的一部分了
同S2
采样核尺寸 2 × 2 2\times2 2×2
步长stride为2
无填充padding
输出特征图的尺寸 10 − 2 + 0 2 + 1 = 5 \frac{10-2+0}{2}+1=5 210−2+0+1=5,所以输出特征图的尺寸是 16 × 5 × 5 16\times5\times5 16×5×5
需要训练的参数是 16 × 2 = 32 16\times2=32 16×2=32个(原因和S2相同)
C5:
卷积核个数120个
卷积核尺寸 5 × 5 5\times5 5×5(这里每个卷积核的深度就和输入图的深度一样了,即每个卷积核实际上是 16 × 5 × 5 16\times5\times5 16×5×5)
步长为1
无填充padding
输出特征图尺寸 5 − 5 + 0 1 + 1 = 1 \frac{5-5+0}{1}+1 = 1 15−5+0+1=1,所以最终输出特征图的尺寸是 120 × 1 × 1 120\times 1\times1 120×1×1,就相当于一个 120 × 1 120\times 1 120×1的列向量
需要训练的参数个数为 120 × ( 16 × 5 × 5 + 1 ) = 48120 120\times(16\times5\times5+1)=48120 120×(16×5×5+1)=48120
F6:
全连接层84个节点
上一层120个节点全连接
总共需要训练的参数个数为 ( 120 + 1 ) × 84 = 10164 (120+1)\times84=10164 (120+1)×84=10164
Output
最后要预测10个类别嘛,所以最后一层肯定10个节点,和上一层的84个节点全连接
除了采样层和最后一层输出层,卷积层和全连接层的激活函数采用了下面的形式
f ( a ) = A t a n h ( S a ) f(a) = A\quad tanh(Sa) f(a)=Atanh(Sa)
输出层采用RBF径向基函数做输出
y i = ∑ j ( x j − w i j ) 2 y_i = \sum_j(x_j-w_{ij})^2 yi=j∑(xj−wij)2
就是用上一层的输入和对应权重求一个欧氏距离
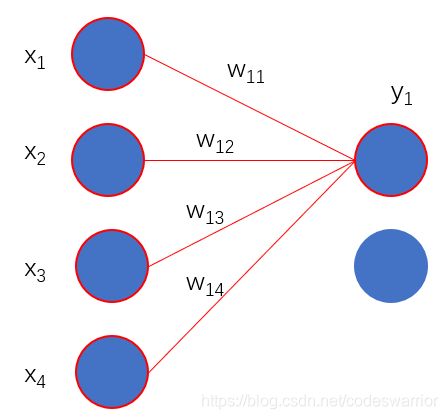
图9
当然现在大部分实现LeNet网络并没有像论文中那么复杂,C3单纯使用的是 6 × 5 × 5 6\times5\times5 6×5×5的卷积核,使用max pooling作为pooling层,激活函数使用ReLu,最后一层全连接层也和前面一样,最后使用交叉熵作为损失函数。
下面是Pytorch的实现,来自Pytorch官网的tutorials
Code:
import torch.nn as nn
import torch.nn.functional as F
# 定义网络
class LeNet(nn.Module):
def __init__(self):
super(LeNet, self).__init__()
self.conv1 = nn.Conv2d(3, 6, 5)
self.pool = nn.MaxPool2d(2, 2)
self.conv2 = nn.Conv2d(6, 16, 5)
self.fc1 = nn.Linear(16 * 5 * 5, 120)
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 10)
def forward(self, x):
x = self.pool(F.relu(self.conv1(x)))
x = self.pool(F.relu(self.conv2(x)))
x = x.view(-1, 16 * 5 * 5)
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
return x
# 指定loss和优化
import torch.optim as optim
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(net.parameters(), lr=0.001, momentum=0.9)