把 WaveGlow 拆开来看

本来要学习 WaveGlow，但是越看越晕，很多博客又绕出了很多新的概念，即基于流的生成式网络 Glow ，以及那些不是基于流的生成网络的介绍如 GAN 和 VAE 等，所以在学习 WaveGlow 之前就得先学习这些概念，妈呀……

在 Glow 论文之前，又有两个基于流的生成模型 NICE 和 RealNVP，这两个是 Glow 的基石。

Generative Model

生成式模型是什么？给出的一般的未标记的数据点，一个生成式模型会尝试去学习什么样的概率分布会生成这些数据点，目的是为了通过利用学习分布来产生新的数据点（与输入数据点相似）。
一个生成式模型是显式建模模型的话，意味着我们明确的定义概率分布并尝试去适配每一个输入的未标记数据点。与它形成对比，一个隐式生成式模型学习一个概率分布，可以直接取样新数据点而不需要明确的定义。GANs（生成对抗网络），目前深度学习领域的圣杯，就属于隐式生成式模型。然而，WaveNet和它的表亲Pixel CNNs/RNNs（像素卷积神经网络模型/递归神经网络模型） 都属于显式生成式模型。

生成式网络有四个分类：

1. Component by Component （也就是 Regressive model 即自回归网络，生成一幅图片的过程是一个像素一个像素地生成）
2. Variational Auto Encoder
3. GAN（Generative Adversarial Network 即大名鼎鼎的生成对抗网络）
4. Flow-based Generative Model 即基于流的生成式模型

基于流的生成模型可以大致理解为：它希望将数据表示成简单的隐变量分布，并可以从该分布中完全还原真实数据的分布。也就是说，它要学习一个可逆函数。利用雅克比矩阵的这个性质：一个函数的雅克比矩阵的逆矩阵，是该函数的反函数的雅克比矩阵。

补充知识：WaveNet

WaveGlow 的模型构建综合参考了 WaveNet 和 Glow，所以在实现的时候使用到了WaveNet的网络，之前不太了解，就另外看了一下。

WaveNet预测的直接是时域上的音波强度，也就是原始的语音采样。因此有必要了解一下语音的编码形式，语音是使用 16 bits 进行编码的，也就是说一个时间点的音强范围为 $[-2^{15},2^{15}-1]$。然后WaveNet预测的是分类分布，也就是说每一个时间点输出的是语音编码长度的向量，然后使用softmax便可以找出其预测得到的音强。但是预测的向量维度太大，对于语音这种采样率这么高的数据，会占用很多的资源，所以需要对编码输出进行压缩。

WaveNet中采用的是 $\mu$ 律压缩，公式为：

代码实现如下：
$$\begin{gathered} f(x_t)=sign(x_t)\frac{ln(1+\mu |x_t|)}{ln(1+\mu )} \\ {y}_t=\frac{f(x_t)+1}{2}\ast \mu \\ 其中的x_t为语音音强除以2^{15}归一化后的结果，\mu 为255 \end{gathered}$$

def mu_law(x, mu=255):
    x = numpy.clip(x, -1, 1)
    x_mu = numpy.sign(x) * numpy.log(1 + mu*numpy.abs(x))/numpy.log(1 + mu)
    return ((x_mu + 1)/2 * mu).astype('int16')

# mu law前先将数据归一化，即幅值范围下降
ret = [mu_law(x / 2 ** 15) for x in used_data] 
ret = numpy.array(ret,dtype=numpy.float)
print(max(ret),min(ret))

plt.figure(figsize=(12, 8))
librosa.display.waveplot(ret, sr=16000)
plt.xlim(0, 1)
plt.tight_layout()

WaveGlow

基础知识

要学明白WaveGlow，首先要知道三件事：

1. Jacobian(雅可比矩阵)：
   $$\begin{gathered} z=\left[\begin{array}{c}{z}_1\\ z_2\end{array}\right],x=\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right] \\ x=f(z) \\ 那么函数f的雅可比矩阵为： \\ {J}_f=\left[\begin{array}{cc}\partial x_1/\partial z_1& \partial x_1/\partial z_2\\ \partial x_2/\partial z_1& \partial x_2/\partial z_2\end{array}\right] \\ 另外函数f的反函数f^{-1}的雅可比矩阵为： \\ {J}_{f^{-1}}=\left[\begin{array}{cc}\partial z_1/\partial x_1& \partial z_1/\partial x_2\\ \partial z_2/\partial x_1& \partial z_2/\partial x_2\end{array}\right] \\ 而上面的两个雅可比乘起来的话，可以得到单位矩阵，也就是说明上面两个矩阵互为逆矩阵 \end{gathered}$$

2. Determinant(行列式)：行列式计算得到一个scalar。另外很重要的一个公式是：
   $$\begin{gathered} det(A)=\frac{1}{det(A^{-1})} \\ det(J_f)=\frac{1}{det(J_{f^{-1}})} \end{gathered}$$
   其实行列式是有含义的：行列式代表了高维空间中的体积的概念
   

3. Change of Variable Theorem：给定输入的分布和输出的分布，找出两者之间的转换关系
   
   
   

代码解读

代码参考的是 NVIDIA实现的版本，仓库地址在这里。后面代码的解读都是基于这个实现。

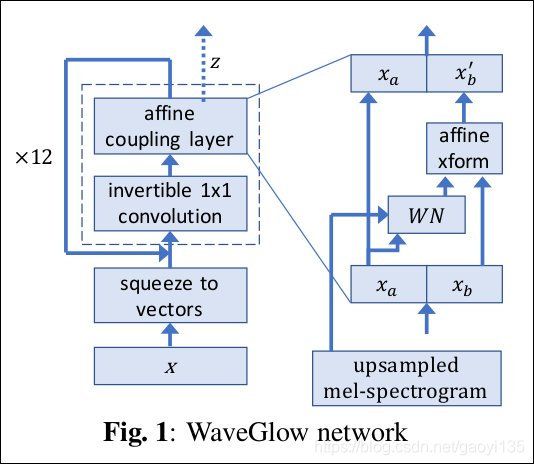
模型的输入：mel spectrum + audio （推理的时候只需要输入mel spectrum）

模型的输出：根据mel spectrum 生成的语音信号

下面以模型 inference 的过程讲述代码逻辑以及网络结构的解读：

# 假设现在输入的 mel spectrum 的维度为 [B, 80, 190] (190为要生成语音的那句话文本经过Tacotron2后得到的mel spectrum 序列长度)
# 根据 WaveNet，输入的这一段 mel spectrum 是需要作为 local conditioning 输入到 WN 网络中去运算的，也就是论文中所说的“By conditioning the model on other input variables, we can guide WaveNet's generation to produce audio with the required characteristics”
# 输进去的mel spectrum 会经过采用转置卷积的上采样
spect = torch.nn.ConvTranspose1d(n_mel_channels, n_mel_channels, kernel_size=1024, stride=256) # 对应论文中的“we first transform this time series using a transposed convolutional network(learned upsample) that map it to a new time series y=f(h) with the same resolution as the audio signal” 
# spect 序列的长度经过上采样之后，会被修剪为对应的audio的长度，接着会被unfold成８份，然后变成 [B, 8*80, audio_length]这样的数据规格，这一步的转换明显是根据mel 频谱和对应的audio的长度做的转变
# 接着初始化一个norm分布的逆过程的输入的z变量即audio，这里的self.n_remaining_channels＝４是训练是最后一层的输出channels，其实self.n_remaining_channels最开始是等于n_group也就是8，但是因为waveglow采用的early output机制，其每经过4个flow就先输出2个channels，因此12个flows就会有两次提前输出到机会，于是最后的self.n_remaining_channels=8 -2 -2=4。因为现在是inference过程，所以反着来，
audio = torch.cuda.FloatTensor(spect.size(0), self.n_remaining_channels, spect.size(2)).normal_()
# 之后经过flows的过程也是和训练过程相反的
for k in reversed(range(self.n_flows)):
	n_half = int(audio.size(1)/2)
    audio_0 = audio[:, :n_half, :]
    audio_1 = audio[:, n_half:, :]
    output = self.WN[k]((audio_0, spect)) # 注意：输入到WaveNet中的是前半段audio_0和spect
    s = output[:, n_half:, :]
    b = output[:, :n_half, :]
    
    audio_1 = (audio_1 - b) / torch.exp(s)
    audio = torch.cat([audio_0, audio_1], dim=1)
    audio = self.convinv[k](audio, reverse=True) # 就连耦合层与1x1卷积层的顺序也要反着来
    # 下面的这一段也很有意思，在训练的时候，我们是每经过４个flows就先将两个channels输出来，也就是channels数会变少，而inference的时候则相反，我们要给audio信号增加两个channels
    if k % self.n_early_every == 0 and k > 0:
        z = torch.cuda.FloatTensor(spect.size(0), self.n_early_size, spect.size(2)).normal_()
        audio = torch.cat((sigma*z, audio), 1)

# 反着经过12个flows之后，得到的audio输出需要转为[B, audio_length]的格式，也就是语音信号
audio = audio.permute(0,2,1).contiguous().view(audio.size(0), -1).data
# 又因为我们这里生成的audio数据是经过u律压缩的8bits，所以还需要后处理将8bits的数据恢复到16bits
waveform = (audio*32000).squeeze() # 因为以上生成的audio的数值都比较小，为了还原到原始16bits的数值的话，乘以一个32000
waveform = np.clip(waveform, -32768, 32767) # 超过两个边界值的统一置为边界值
waveform = waveform.astype(np.int16)
# 最后还有一步是调节生成的语音信号的速度、音量以及音调

以上就是WaveGlow根据Tacotron2生成语音信号的全流程了，现在唯一不理解的就是 WaveNet 的网络结构了。WaveNet 的网络在 WaveGlow 中充当了 耦合层的角色，使得前后运算可逆。下面扒一扒WaveNet的内部实现：

对于mel spectrum在WN中的作用请看下面WaveNet中的这段描述（文中的$h_t$对应的就是代码中的mel spectrum）：

注意下面这个图是在WaveNet中的结构图，WaveGlow中的实现与其很不一样的，其实WaveGlow的WN结构中并没有用到因果卷积这种东西，因为因果卷积是用在自回归模型中的，而WaveGlow可以实现并行计算。

'''
WN_config: {"n_layers":8, "n_channels":256, "kernel_size":3}
'''
'''
def fused_add_tanh_sigmoid_multiply(input_a, input_b, n_channels):
	n_channels_int = n_channels[0]
	in_act = input_a + input_b
	t_act = torch.tanh(in_act[:, :n_channels_int :]) # 注意两个激活函数使用的通道是不同的
	s_act = torch.sigmoid(in_act[:, n_channels_int:, :])
	acts = t_act * s_act
	return acts
'''

# 注意输入到WN网络中的是完整audio的half，理解这个需要学习耦合层
def WN(audio, spect):
	audio = self.start(audio)  # self.start()是一个Conv1d一维卷积层，audio的维度从[B, 2, audio_length]变成[B, 256, audio_length] 也就是WaveNet网络中的channels数
    out_put = torch.zeros_like(audio)  # 先构造一个全零的
    spect = torch.nn.Conv1d(spect.size(1), 2*n_channels*n_layers, 1) # 这里做卷积也就对应与上面论文截图中的对y的卷积操作，输出维度里面有一个乘以 n_layers 的操作，也就意味着WN的每一层参与运算的spect是不同的，后面会做切片处理平均分给每层
    for i in range(self.n_layers):
        spect_offset = i*2*self.n_channels
        acts = fused_add_tanh_sigmoid_multipy(  # 这个函数实现的就是上面截图中的公式，具体定义看上面
        	self.in_layers[i](audio),　# in_layers[i] = torch.nn.Conv1d(n_channels, 2*n_channels, kernel_size, dilation=2**i, padding =int((kernel_size*dilation-dilation)/2))
            spect[:, spect_offset:spect_offset+2*self.n_channels, :],
            n_channels_tensor) # n_channels_tensor就是一个值为256的tensor
       	res_skip_acts = self.res_skip_layers[i](acts) # 这里的self.res_skip_layers[i]同样是一个Conv1d一维卷积层
        if i < self.n_layers-1:　# 最后一层前res_skip_acts输出的维度为2*self.n_channels，一般用于直接加到输出上，一般加到audio中
            audio = audio + res_skip_acts[:, :self.n_channels, :]
            output = output + res_skip_acts[:, self.n_channels, :]
        else:
            output = output + res_skip_acts
    return self.end(output)  # self.end与self.start一样，是一位卷积层，输入输出维度是(n_channels, 2*n_in_channels) 这里返回的2*n_in_channels会被分成 s 和 t 两部分，用于audio_1 的仿射变换。

损失函数

最后我们再来聊一聊WaveGlow的损失函数：

也就是说，模型整体的损失函数由三部分组成：一是训练过程中生成的 z ，二是仿射变换层的 log(s)，三是 1x1 卷积层的卷积核参数W的行列式。至于为什么是这样，请详细推理过程请参考参考资料中的 “李宏毅教学视频” 。

代码实现的话跟公式是一样的，即优化的是上面公式计算出来的损失乘以-1，也就是负的最大似然。

class WaveGlowLoss(torch,nn.Module):
    def __init__(self, sigma=1.0):
        super(WaveGlowLoss, self).__init__()
        self.sigma = sigma
    def forward(self, model_output):
        z, log_s_list, log_det_W_list = model_output # 这是在训练过程中存下来的，log_s_list是每一层的s，log_det_ｗ_list是每一个1x1层的卷积核参数
        for i, log_s in enumerate(log_s_list):
            if i==0:
                log_s_total = torch.sum(log_s)
                log_det_W_total = log_det_W_list[i]
            else:
                log_s_total = log_s_total + torch.sum(log_s)
                log_det_W_total += log_det_W_list[i]
        loss = torch.sum(z*z)/(2*self.sigma*sigma) - log_s_total - log_det_W_total
        return loss/(z.size(0)*z.size(1)*z.size(2)) # 求平均

参考资料

李宏毅教学视频
音频处理时的mu law与反mu law变换
一文带你读懂 WaveNet：谷歌助手的声音合成器