CART回归树及其实战
1.CART简介
分类与回归树(classification and regression tree,CART)模型由Breiman等人在1984年提出,是应用广泛的决策树学习方法。CART同样由特征选择而、树的生成及剪枝组成,既可以用于分类也可以用于回归。
2.基本概念
CART假设决策树是二叉树,内部结点特征的取值为“是”和“否”,左分支是取值为“是”的分支,右分支是取值为“否”的分支。这样的决策树等价于递归地二分每个特征,将输入空间即特征空间划分为有限个单元,并在这些单元上确定预测的概率分布,也就是在输入给定的条件下输出的条件概率分布。
CART算法由以下两步组成:
(1)决策树的生成:基于训练数据集生成决策树,生成的决策树要尽量大(大是为了更好地泛化);
(2)决策树剪枝:用验证数据集对已生成的树进行剪枝并选择最优子树,这时损失函数最小作为剪枝的标准。
3.CART树生成
3.1回归树的生成
在训练数据集所在的输入空间中,递归地将每个区域划分为两个子区域并决定每个子区域上的输出值,构建二叉决策树。
(1)选择最优切分变量j与切分点s,求解
min j , s [ min c 1 ∑ x i ∈ R 1 ( j , s ) ( y i − c 1 ) 2 + min c 2 ∑ x i ∈ R 2 ( j , s ) ( y i − c 2 ) 2 ] \underset{j,s}{\mathop{\min }}\,\left[ \underset{{{c}_{1}}}{\mathop{\min }}\,\sum\limits_{{{x}_{i}}\in {{R}_{1}}\left( j,s \right)}{{{\left( {{y}_{i}}-{{c}_{1}} \right)}^{2}}}+\underset{{{c}_{2}}}{\mathop{\min }}\,\sum\limits_{{{x}_{i}}\in {{R}_{2}}\left( j,s \right)}{{{\left( {{y}_{i}}-{{c}_{2}} \right)}^{2}}} \right] j,smin⎣⎡c1minxi∈R1(j,s)∑(yi−c1)2+c2minxi∈R2(j,s)∑(yi−c2)2⎦⎤
遍历变量j,对固定的切分变量j扫描切分点s,选择使上式达到最小值的对(j,s)j。
(2)用选定的对(j,s)划分区域并决定响应的输出值:
R 1 ( j , s ) = { x ∣ x ( j ) ≤ s } , R 2 ( j , s ) = { x ∣ x ( j ) > s } {{R}_{1}}\left( j,s \right)=\left\{ x\left| {{x}^{\left( j \right)}} \right.\le s \right\},{{R}_{2}}\left( j,s \right)=\left\{ x\left| {{x}^{\left( j \right)}} \right.>s \right\} R1(j,s)={x∣∣∣x(j)≤s},R2(j,s)={x∣∣∣x(j)>s}
c ^ m = 1 N m ∑ x i ∈ R m ( j , s ) y i , x ∈ R m , m = 1 , 2 {{\widehat{c}}_{m}}=\frac{1}{{{N}_{m}}}\sum\limits_{{{x}_{i}}\in {{R}_{m}}\left( j,s \right)}{{{y}_{i}}},x\in {{R}_{m}},m=1,2 c m=Nm1xi∈Rm(j,s)∑yi,x∈Rm,m=1,2
(3)继续对两个子区域条用步骤(1),(2),直至满足停止条件。
(4)将输入空间划分为M个区域 R 1 , R 2 , . . . , R M {{R}_{1}},{{R}_{2}},...,{{R}_{M}} R1,R2,...,RM,生成决策树:
f ( x ) = ∑ m = 1 M c ^ m I ( x ∈ R m ) f\left( x \right)=\sum\limits_{m=1}^{M}{{{\widehat{c}}_{m}}I\left( x\in {{R}_{m}} \right)} f(x)=m=1∑Mc mI(x∈Rm)
3.2回归树生成的例子
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| y | 5.56 | 5.70 | 5.91 | 6.40 | 6.80 | 7.05 | 8.90 | 8.70 | 9.00 | 9.05 |
当s=1.5时 R 1 = { 1 } , R 2 = { 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 } {{R}_{1}}=\left\{ 1 \right\},{{R}_{2}}=\left\{ 2,3,4,5,6,7,8,9,10 \right\} R1={1},R2={2,3,4,5,6,7,8,9,10}
c 1 = 5.56 , c 2 = 1 9 ( 5.70 + 5.91 + 6.40 + 6.80 + 7.05 + 8.90 + 8.70 + 9.00 + 9.05 ) = 7.50 {{c}_{1}}=5.56,{{c}_{2}}=\frac{1}{9}\left( 5.70+5.91+6.40+6.80+7.05+8.90+8.70+9.00+9.05 \right)=7.50 c1=5.56,c2=91(5.70+5.91+6.40+6.80+7.05+8.90+8.70+9.00+9.05)=7.50
m ( 1.5 ) = 0 + 15.72 = 15.72 m\left( 1.5 \right)=0+15.72=15.72 m(1.5)=0+15.72=15.72
| s | 1.5 | 2.5 | 3.5 | 4.5 | 5.5 | 6.5 | 7.5 | 8.5 | 9.5 |
| c1 | 5.56 | 5.63 | 5.72 | 5.89 | 6.07 | 6.24 | 6.62 | 6.88 | 7.11 |
| c2 | 7.5 | 7.73 | 7.99 | 8.25 | 8.54 | 8.91 | 8.92 | 9.03 | 9.05 |
| m(s) | 15.72 | 12.07 | 8.36 | 5.78 | 3.91 | 1.93 | 8.01 | 11.73 | 15.74 |
显然s=6.5时,c1=6.24,c2=8.91,m(s)最小。因此j=x,s=6.5,回归树 f 1 ( x ) {{f}_{1}}\left( x \right) f1(x)为:
f 1 ( x ) = { 6.24 , x ≤ 6.5 8.91 , x > 6.5 {{f}_{1}}\left( x \right)=\left\{ \begin{matrix} 6.24,x\le 6.5 \\ 8.91,x>6.5 \\ \end{matrix} \right. f1(x)={6.24,x≤6.58.91,x>6.5
对 x ≤ 6.5 x\le 6.5 x≤6.5部分进行划分,回归树 f 2 ( x ) {{f}_{2}}\left( x \right) f2(x)为:
f 2 ( x ) = { 5.72 , x ≤ 3.5 6.75 , 3.5 < x ≤ 6.5 8.91 , x > 6.5 {{f}_{2}}\left( x \right)=\left\{ \begin{matrix} 5.72,x\le 3.5 \\ 6.75,3.5<x\le 6.5 \\ 8.91,x>6.5 \\ \end{matrix} \right. f2(x)=⎩⎨⎧5.72,x≤3.56.75,3.5<x≤6.58.91,x>6.5
依此类推 x > 6.5 x>6.5 x>6.5部分,之后不断重复直到满足条件(树的深度、树的叶子个数等都可以作为停止条件)
4.实战
(1)max_depth=1, max_leaf_nodes=3的情况
from sklearn.tree import DecisionTreeRegressor
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
X = np.array(list(range(1, 11))).reshape(-1,1)
y = np.array([5.56, 5.70, 5.91, 6.40, 6.80, 7.05, 8.90, 8.70, 9.00, 9.05]).ravel()
model = DecisionTreeRegressor(max_depth=1,max_leaf_nodes=3)
model.fit(X,y)
plt.scatter(X, y, s=20)
plt.plot(X,model.predict(X),color='blue')
![]()
(2)max_depth=2, max_leaf_nodes=5的情况
model = DecisionTreeRegressor(max_depth=2,max_leaf_nodes=5)
model.fit(X,y)
plt.scatter(X, y, s=20)
plt.plot(X,model.predict(X),color='blue')
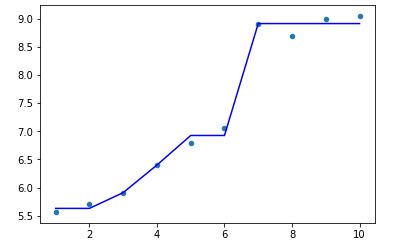
回归树的一些参数设置可以参考之前我写的决策树文章。
5.总结
5.1分类树
以C4.5分类树为例,C4.5分类树在每次分枝时,是穷举每一个feature的每一个阈值,找到使得按照feature<=阈值,和feature>阈值分成的两个分枝的熵最大的阈值(熵最大的概念可理解成尽可能每个分枝的男女比例都远离1:1),按照该标准分枝得到两个新节点,用同样方法继续分枝直到所有人都被分入性别唯一的叶子节点,或达到预设的终止条件,若最终叶子节点中的性别不唯一,则以多数人的性别作为该叶子节点的性别
分类树使用信息增益或增益比率来划分节点;每个节点样本的类别情况投票决定测试样本的类别。
5.2回归树
回归树总体流程也是类似,区别在于,回归树的每个节点(不一定是叶子节点)都会得一个预测值,以年龄为例,该预测值等于属于这个节点的所有人年龄的平均值。分枝时穷举每一个feature的每个阈值找最好的分割点,但衡量最好的标准不再是最大熵,而是最小化均方差即(每个人的年龄-预测年龄)^2 的总和 / N。也就是被预测出错的人数越多,错的越离谱,均方差就越大,通过最小化均方差能够找到最可靠的分枝依据。分枝直到每个叶子节点上人的年龄都唯一或者达到预设的终止条件(如叶子个数上限),若最终叶子节点上人的年龄不唯一,则以该节点上所有人的平均年龄做为该叶子节点的预测年龄。
回归树使用最大均方差划分节点;每个节点样本的均值作为测试样本的回归预测值。
参考文章:
李航《统计学习方法》
https://blog.csdn.net/weixin_40604987/article/details/79296427#commentBox
https://blog.csdn.net/puqutogether/article/details/44593647